最简单的讲解：梯度下降法

前言

目前网上的一些博客讲解的太笼统了，没有讲解原理，让人一头雾气。梯度下降法其实还是比较简单的下降法，因为还有其他下降法，这些都是在数值分析课程中讲解的，悔恨啊，数值分析上过两次课，还是没听懂，现在才知道原来在机器学习中这么常用，本文从多个角度来讲解梯度下降法，帮助大家理解

简单的一元函数

所有的问题都是从简单到复杂，一步一步来解决复杂问题的，我们首先看下一元函数的情况，这个一元函数是专门为了讲解知识而构造的一个，没有其他含义，我们假设有一个函数$y=2x^2+2$，求解这个函数的最小值，如何求解？首先看下这个图像

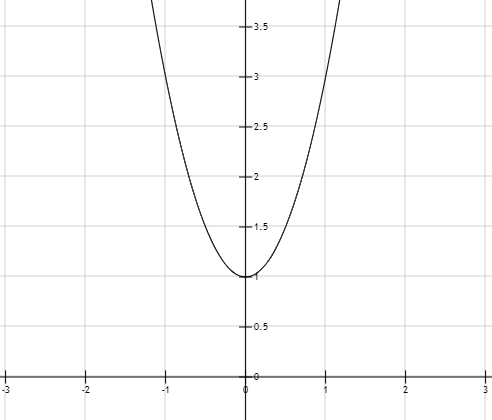
第一种方式：求极值

求极值使我们通用的方式，极值点可能是最小值点，所以，我们可以通过求解该函数的所有极值点，比较极值点的$y$来得到最小值点，于是求解过程如下：

• 先求导数：$y^{{}^{\prime }}=4x$
• 令导数等于0，及$y^{{}^{\prime }}=4x=0$ 得出 $x=0$
• 第二步中我们得到了极值点， $x=0$就一个极小值点，所以这个点是一个最小值点

这样做可以直接求出最小值，也就自然可以知道对应$x$，我们可以看下另一个角度下的问题。

另一个角度

如果导数=0求解比较复杂，也就是难以直接求解出$x$，我们采取另一种方式，对于一元函数来讲，对于某个坐标点的导数是确定的，比如上述导数$y^{{}^{\prime }}=4x$，在x=1这个点，导数就等于4，而且导数是有方向性的：
$$y=\{\begin{array}{ll}越小& \text{y‘<0，x越大}\\ 越大& \text{y‘>0，x越大}\end{array}$$
利用这个性质，我们可以来改变x的值，使它不停的向极值点靠近，我们希望它向极小值点靠近，这样就可以使y有一个极小值，如何操作：

• 1、设定一个初始化的x的值和步长$\alpha$
• 2、求得导数$y^{{}^{\prime }}$
• 3、更新x，$x=x-\alpha y^{{}^{\prime }}(x)$ ，y^{’}(x)表示导数在x处的具体值，
• 4、用更新后的$x$来计算$y$值，
• 5、比较y跟之前的y值大小关系，如果更新后的$y$更小，重复3、4、5步骤，否则停止。

经过上述步骤后，我们最终可以得到一个极小值，但极小值不一定是最小值。严谨一点的算法步骤总结如下：

• 1、设定一个初始化的$x_1$、$y_1$、步长$\alpha$、判断条件$\theta$
• 2、更新$x$，$x_{i+1}=x_i-\alpha y^{{}^{\prime }}(x_i)$ ，y^{’}(x_i)表示导数在$x_i$处的具体值，初始时$i=1$
• 3、用更新后的$x_{i+1}$来计算$y_{i+1}$值
• 4、比较$y_{i+1}$跟之前的$y_i$值大小关系，如果更新后的$y$更小，重复3、4、5步骤，否则停止

$$\{\begin{array}{ll}{y}_i-y_i>\theta & \text{重复步骤2、3、4}\\ & \\ y_i-y_i<=\theta & \text{终止}\end{array}$$
因为有可能$x$收敛到一定的地步后，y也取到了最小值，有时候并不追求过分的最小值，所以我们可以通过$\theta$来控制，只要与上一次的y值比较，他们之间的差小于$\theta$，就说明已经很接近最小值了，收敛已经非常慢了，一般$\theta$ 也是非常小的。步长$\alpha$也是一个用来控制收敛速度的参数，这个一般是$\alpha =0.01$，也是非常小的，大一些也没有问题，收敛速度会非常快，但是很大的时候没有什么好的作用，反而不会收敛，待会会讲到这个问题。

泰勒公式角度

首先要明确一个概念，就是所有的函数都可以被泰勒展开式代替，所以：
$$f(x)=f(x_0)+\frac{f^{{}^{\prime }}(x_0)}{1!}(x-x_0)+\frac{f^{{}^{\prime \prime }}(x_0)}{2!}(x-x_0{)}^2+\frac{f^{{}^{\prime \prime \prime }}(x_0)}{3!}(x-x_0{)}^3+...$$
你一直计算到n阶，这个泰勒公式的精确度越高，我们这里取一阶，也就是：
$$f(x)=f(x_0)+\frac{f^{{}^{\prime }}(x_0)}{1!}(x-x_0)=f(x_0)+f^{{}^{\prime }}(x_0)(x-x_0)$$
我们的目标是希望迭代过程中函数值会逐渐减小，通过不断的更新$x_i$值，使得$f(x_i)$越来越小，最终收敛到一个范围内。所以假设：
$$\begin{gathered} \Delta x=x-x_0=-f^{{}^{\prime }}(x_0) \\ f(x)=f(x_0)-f^{{}^{\prime }}(x_0{)}^2 \end{gathered}$$
这样$f(x)$就不断的变小，所以
$$\begin{gathered} x-x_0=-f^{{}^{\prime }}(x_0) \\ x=x_0+-f^{{}^{\prime }}(x_0) \end{gathered}$$
所以可以通过不断的更新$x$值来得到最终符合条件的$f(x)$。算法步骤类似于上一节的内容，这里就不赘述了.

复杂的多元函数

参考博客

tensorflow-梯度下降,有这一篇就足够了