目录
量化的原则:
量化是把一个函数的无限个数值的集合映射为一个离散函数的有限个数值的集合,通常采用四舍五入的原则进行数值量化;
是不是量化间隔越小越好呢?
确定后的量化取值叫量化值,

量化值的个数称为量化级,

相邻两个量化值之差就是量化间隔,

从前面我们可以看到,v(t)的样值信号k(t)和量化后的样值信号m(t)是不一样的,

比如k(0)=0.2, m(0) = 0,而收信端恢复的信号是量化后的信号m(t),而不能恢复出k(t),这样就使得收发的信号之间有误差,

显然,这种收发误差是由量化引起的,我们称其为量化误差,或量化噪声,
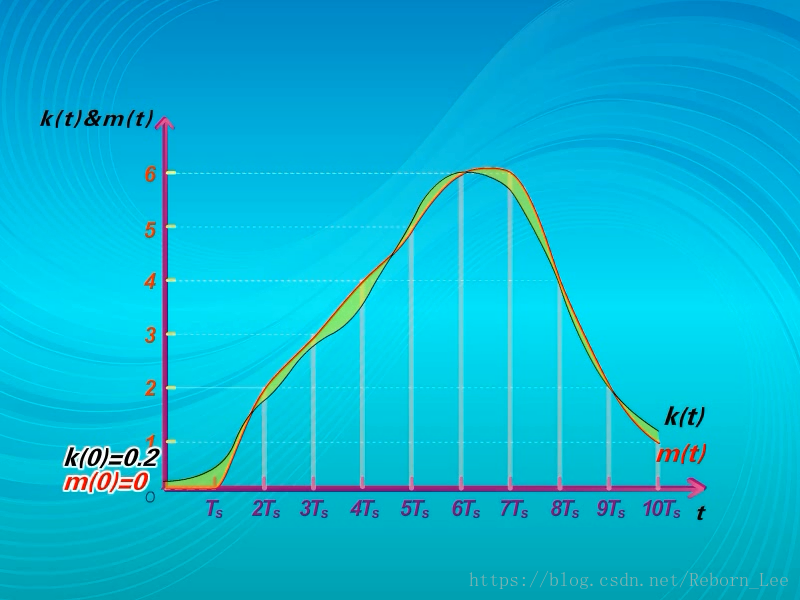
比如,上例中,量化间隔为1,由于采用四舍五入量化,因此量化噪声的最大值为0.5;

均匀量化
一般来说,量化间隔都一样的量化叫做均匀量化;

那么如果在一定的取值范围内,把量化值多取几个,也就是把量化间隔变小,则量化噪声就会减小,比如:
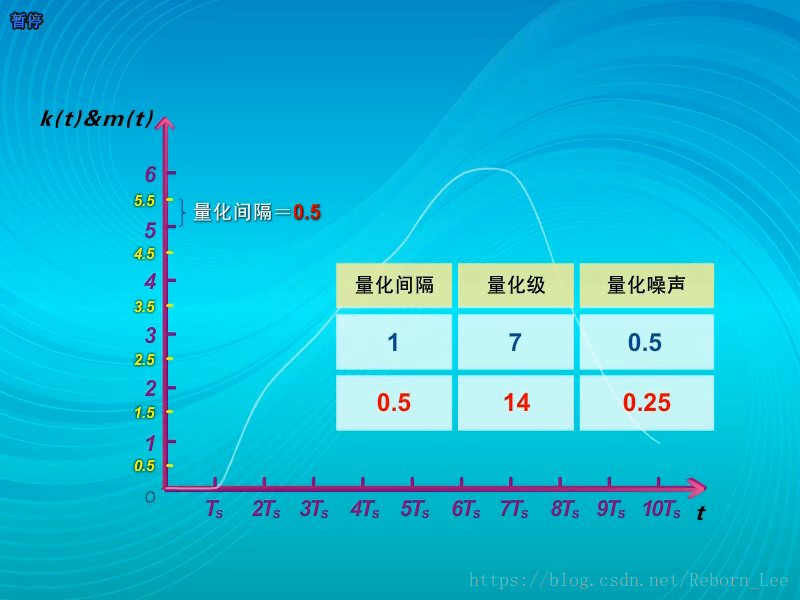
显然量化噪声与量化间隔成正比,量化间隔越小,量化噪声越小,但在实际中,不可能对量化分级过细,因为过多的量化值将直接导致系统的复杂性和经济型,可靠性,方便性,维护使用性等指标的恶化。
问题:尽管信号幅值大,和信号幅值小,使得绝对量化噪声是一样的,都是0.5个量化间隔,但相对误差却悬殊很大,也就是说对信号的影响大小并不一样,比如上例中,


相对误差的科普:
相对误差指的是测量所造成的绝对误差与被测量(约定)真值之比乘以100%所得的数值,以百分数表示。一般来说,相对误差更能反映测量的可信程度。设测量结果y减去被测量约定真值t,所得的误差或绝对误差为Δ。将绝对误差Δ除以约定真值t即可求得相对误差。
相对误差大,意味着小信号的信噪比小,能否找到了一种方法既提高了小信号的信噪比,又不过多的增加量化级,细化量化间隔?
非均匀量化
非均匀量化法登场:

实现这种思路的方法是压缩与扩张,如下图,脉冲A和脉冲B是两个样值,作为压缩器的输入信号,通过压缩后变为 和
和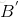 ;
;

可见, 与A基本上没有变化,而
与A基本上没有变化,而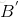 却比B大了许多,这正是我们需要的压缩特性,在收信端
却比B大了许多,这正是我们需要的压缩特性,在收信端 和
和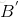 作为扩张器的输入信号,经扩张后还原为样值A和样值B,
作为扩张器的输入信号,经扩张后还原为样值A和样值B,

现在我们来看一下,小信号的信噪比的变化情况,在下图中,没有经过压缩器的相对误差为1/2,经过压缩器后的相对误差为1/6,可见相对误差减小了,这也就意味这信噪比增大了。

压缩特性经常采用对数压缩特性,也就是压缩器的输出与输入之间,近似成对数关系,对电话信号而言,对数压缩特性又分为:

我国采用A律。
因此可以在抽样器后面加上一个叫压缩器的信号处理电路,

该电路的特点是对弱小信号有比较大的放大倍数,而对大信号的增益却比较小,抽样后的信号经过压缩器后就发生了畸变,大信号部分与进压缩器前差不多,没有得到多少增益,而弱小信号部分却得到了不正常的放大,相比之下,大信号好像被压缩了,压缩器由此而得名;

对压缩后的信号再进行均匀量化,就相当于对抽样信号进行了非均匀量化,那么,在收信端为了恢复原始抽样信号,就必须把接收到的经过压缩的信号,还原成压缩前的信号,完成这个还原过程的电路就是扩张器,

它的特性正好与压缩器相反,对小信号压缩,对大信号提升;

为了保证信号的不失真,要求压缩特性与扩张特性合并后为一条直线,


也就是说信号通过压缩再通过扩张,实际上好像通过了一个线性电路,显然单独的压缩和扩张对信号进行的是非线性变换。

























 6950
6950

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










