n-gram回顾
在上一篇笔记语言模型(一)—— 统计语言模型n-gram语言模型中我们已经了解到了n-gram的不足,在理解神经网络语言模型之前,我们有必要简单地回顾一下n-gram模型的几个特点:
- 基于统计的语言模型,是一种离散型的语言模型,所以泛化能力差。
- 参数量大,随着 n 的增大,参数空间呈指数增长容易出现维度灾难的问题;巨大的参数量也使得模型无法与n-1个词之外的词建立联系。即不能进行上下文的回溯,不能解决上下文物主代词指代问题。
- 数据稀疏除了带来数据空间增大的问题之外,还有一个问题:无法表征词语之间的相似关系。
NNLM的理解
鉴于上面的问题,人们开始尝试用神经网络来建立语言模型,最经典的无疑是Bengio 的文章A Neural Probabilistic Language Model,文章中提出了如下图所示的前馈神经网络结构:
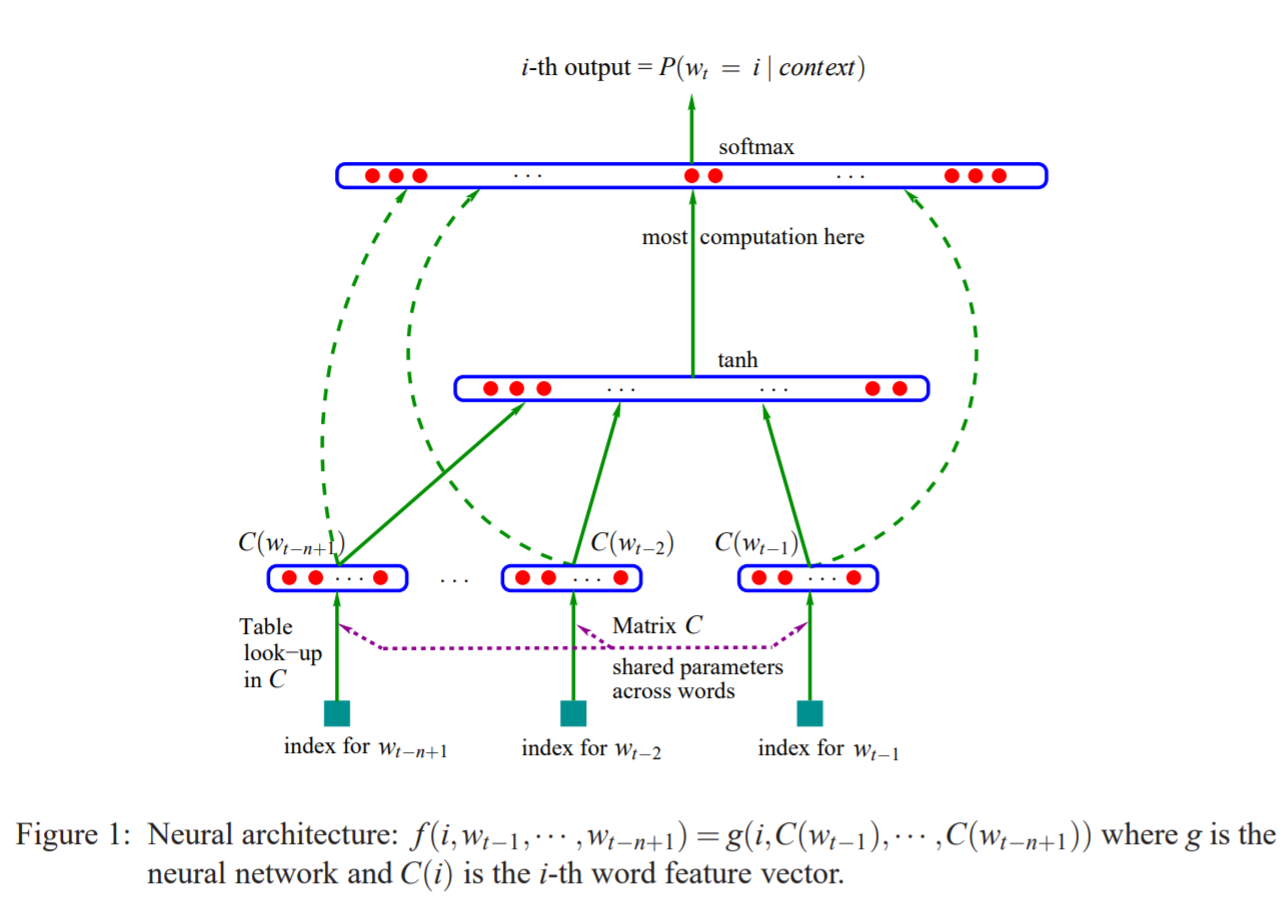
先从整体上看,上述模型属于比较简单而传统的神经网络模型,主要由输入层-隐藏层-输出层组成,经过前向传播和反向传播来进行训练。我个人觉得,理解上面这张图的关键点在于理解词向量,即图中的C(wt-n+1)…C(wt-1)等。那我们就从词向量的映射开始,一层一层往上看。
前向传播
从单词到输入层
在最最开始,我们必须要重提一下语言模型的目的:判断一句话是不是人话。途径是啥?——通过前面的词预测后面的词。而其实神经网络语言模型是基于n-gram演变而来的,即核心是根据前n-1个词预测第n个词,那么我们模型最开始的输入就是前n-1个词。
那么我们又是怎么来表征前n-1个词的呢?答案是词向量。
感觉越说越懵是不是,那么词向量是什么?一个词又是怎么变成词向量的呢?我们慢慢来看。
从Ont-hot到Word Embedding:
词语转化为数字的最简单的形式就是One-hot,简单来说就是假设有一个大小为V的固定排序的词表,里边包含V个词,假设第二个词是“电视”,那么我们用一个维度为V的特征向量表达就是[0,1,0,0,…,0],即该词语在词表中的位置对应在特征向量中的位置的值为1,其他位置都为0。One-hot编码有一个最大的问题就是数据稀疏问题,当词表很大(比如我们现在有一个含80000个词的词表)时,数据稀疏会让整个计算量都变得很大。且词语之间的关联关系得不到表达。
那么词向量(Word Embedding)又是什么呢?人们也叫他词嵌入,就是说我现在不用One-hot那样的稀疏向量来表征我这个词了,我就用一个低维度的向量来表征我这个词,当你很难理解的时候你可以说它是玄学,反正世界上就有这么一个向量能表征我选择的这个词,并且我词表里的每一个词都有对应的表征向量。这个词向量又是怎么取得的呢?
我们给定一个词表征的矩阵C,这个C的维度是V*m,即V行,m列。V是词表的大小,也就是每一行代表了词表里的一个词;m是我们自己定的词向量的维度,比如说对于一个80000个词的词表,原先我要用80000维的One-hot向量来表征“电视”这个词,现在我想就用一个100维的向量来表征,m就是100。(事实上我们常用的就是50或者100)
那么我们用“电视”的One-hot向量[0,1,0,0,…,0]乘以上面说的矩阵C会发生什么?会得到一个m维的向量啊!这就是我们说的词向量,可以看这个过程:

那我们就会想了,你不就是想从C里边取一行么,用的了那么麻烦么,直接给个词在词表中的索引再去C里边按索引取出对应行不就完事了吗?你说的对!你看最开始那张模型图中,作者就是这么干的:

这样我们就得到了前n-1个词的词向量:C(wt-n+1)…C(wt-1);这样我们就完成了从词语到向量的映射。开不开心,但。。。是不是感觉哪里不太对?我们说给定一个矩阵C,这个C怎么来的?事实上,矩阵C是我们随机初始化来的(或者根据一些先验数据初始化来的),也就是说,在神经网络语言模型中,词向量作为一个内部参数,跟神经网络中的其他内部参数一样都是先有一个随机初始化值,正向传播后计算损失函数再反向传播更新这些参数。这也就要求神经网络语言模型是有监督的学习,词向量是学习得到的副产物,也是模型内化的一部分。
词向量全连接作为输入:
得到上面单个词向量之后,我们要将n-1个词向量做一个全连接,即把这n-1个词向量首尾相接地拼起来得到最终的输入x:

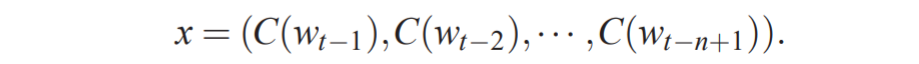
从输入层到隐藏层
这里的隐藏层就是一个很普通的神经网络的做法,权重H乘以输入加上偏置d,再加一个tanh函数作激活函数,就得到了隐藏层:
t a n h ( d + H x ) tanh(d+Hx) tanh(d+Hx)
也就是图中的:

从隐藏层到输出层
我们先计算由隐藏层到输出层未归一化的输出值y1,这里就是一个简单的线性变化:(为了方便理解,这里的描述方式跟原文不太一样,我这里将隐藏层到输出层与输入层到输出层这两部分拆开描述,不影响最后的结果。)
y 1 = U t a n h ( d + H x ) + b 1 y_1=Utanh(d+Hx)+b_1 y1=Utanh(d+








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








