Purpose
To analyse what really matters
One-Way Sensitivity Analysis
Toprank
Base value:最可能的变量值
Low value:最低的变量值
High value:最高的变量值
- 全部变量设置为:Low - Base - High 分别计算outcome
- 其他变量设置为Base value(fixed), 选定的变量分别设置为 [Low, High],得到outcome
- 绘图(Tornado diagram, Spider diagram)

Tornado Diagram
- Purpose: 对多个variable同时进行one-way sensitivity analysis的比较
- Longest bar--- Topest rank---- Most sensitive variable
- 敏感的变量需要重点考虑,其他的leave at their base values
- 横坐标: profit(outcome) ; 纵坐标:rank


Spider Diagram
- Perform a one-way sensitivity analysis for all variables.
- 斜率越大,越敏感


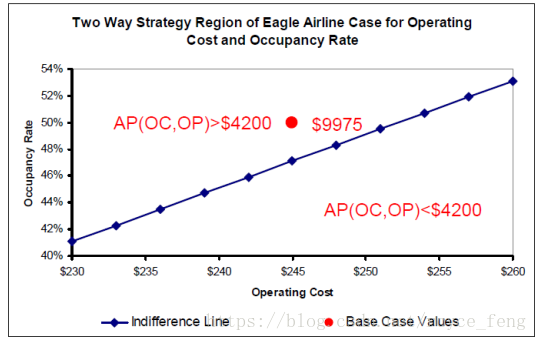
Two-Way Sensitivity Analysis
- 建立公式 Outcome = ......
- 将其他变量取 Base value 得到 Outcome(x1, x2)
- 比较 decision strategy : Outcome(x1, x2) = ..... => x2 = f(x1)
- 绘制 x2 = f(x1)曲线(indifferent curve无差异曲线,在该曲线上,两个decision strategy无差异)
Sensitivity to Probabilities
假设uncertain event 发生的概率,根据决策树求EMV,比较decision strategy画图分析
Example1 :

EMV (purchase) = q(3500r-22500)-11000r+25475
EMV (not purchase) = 4200

Example 2:

(约束:p > 0.15;q > 0.35)


根据上式,画出3条indifferent line


Uncertainty Analysis
根据分布进行仿真优化决策








 本文深入探讨敏感性分析在决策制定中的应用,包括一维和二维敏感性分析的方法,如何通过龙卷风图和蜘蛛图识别关键变量,以及不确定性分析中的仿真优化。通过实例展示如何评估不同决策策略下预期货币价值的变动。
本文深入探讨敏感性分析在决策制定中的应用,包括一维和二维敏感性分析的方法,如何通过龙卷风图和蜘蛛图识别关键变量,以及不确定性分析中的仿真优化。通过实例展示如何评估不同决策策略下预期货币价值的变动。
















 3686
3686

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








