组合导航GPS+IMU

1. 定位技术分类

1.1 基于相对测量的定位（航位推算）

（1）轮式里程计
通过编码器获得轮式里程计的测量数据，车轮的转动被转换成线性位移。对于指定初始位置的运动估计，通过积分得运动增量，从而得到当前的位置信息。
· 该方法具有精度短、成本低、采样率高的优点
· 但车轮会产生打滑，定位误差会随着移动距离增加，影响长期精度
（2）惯性导航
惯性导航系统是自主的，不需要获取外界信息。
惯性传感器（陀螺仪与加速度计）测量角速度与加速度。陀螺仪积分可获得旋转，加速度的一次积分与二次积分分别获得速度与位置。
但积分势必会造成误差的累积。因此低精度的imu，无法单独用于精确定位。

1.2 基于绝对测量的定位

(1) 全球卫星导航系统（GNSS）
GNSS是一种用于室外的导航技术。典型的如：GPS、北斗(中国)、伽利略（欧盟）、GLONASS（俄罗斯）··
通过三边测量，地面接收机可以利用卫星信号的运行时间和当前位置信息来计算其位置，这些信息包含在发射信号中。当接收机与若干卫星的确切距离已知时，就可以计算出接收机的纬度、经度和高度，其中3个是理论上的最小距离，4个可以校正接收机的时钟偏差。只要有足够的卫星覆盖，GPS可为户外导航提供了良好的绝对定位。

(2) 地标导航（Landmark Navigation）
地标导航地标技术用于已知环境下的导航。landmark可以是自然界特定的目标物，也可以是人工地标，可以被检测识别到。因此地标导航需要具备一个保存特征与精确地理位置的数据库。
人工地标是为定位和导航而添加到环境中的物体，而自然地标已经存在于环境中。每个地标必须有一个固定的位置。车辆需要一个关于它们特征和位置的数据库。一些地标可能包括额外的信息，如条形码。车辆必须能够从其传感器输入可靠地识别地标，并以确定其自身位置的方式处理数据。

(3) 基于地图的定位（模板匹配）
当移动设备在某个具有特定地图的环境中运动时，可以使用地图模板匹配。
使用传感器来感知本地环境，然后将感知结果与预存地图进行比较；若匹配成功，则可获得移动设备在具体环境中的位置与方向。通常使用相机与雷达作为该定位技术的传感器。
模板地图需要提前采集，用于室外环境时，通常会与GPS一起使用，以确定设备的路面所在位置。

1.3 组合定位

使用两种及两种以上的定位方法，以获得更可靠的定位信息。

~GPS:
全球定位系统由24颗环绕地球的卫星组成，其平均半径为26.560公里。原则上，GPS接收器只需要三颗卫星的距离，就可以利用三边测量原理计算出它的三维位置。但是需要第四颗卫星来从系统时钟中估计接收机时钟的偏移量。GPS可能会由于信号阻塞、多径效应、干扰而出现中断。例如：城市、峡谷、隧道以及其他市内环境。

为提供更精确的实时定位信息，GPS需要与其他具有互补特性的系统集成，以满足GPS拒止情况下的导航定位。

• GPS增强系统（ 其他GNSS定位系统、空间增强系统、地面增强系统）
• 本地无线定位系统（蜂窝基站、Wi-Fi、电视塔）
• 运动传感器，如惯性传感器，里程表和指南针
• 辅助传感器，如相机、光探测和测距(激光雷达)
• 数字地图

INS与GPS性能

特性	INS	GPS
导航精度	短期精度高，随时间漂移	长期导航精度高，存在噪声干扰
惯性坐标系	使用	不使用
姿态信息	有	没有
感知重力方向	是	否
输出频率	高频	低频
自主	是	否

图1.典型的（INS/GPS）组合导航系统结构图

1.可获得更高精度的位置与速度
2.可以得到姿态信息
3.较高的数据输出频率
4.解决GPS信号阻塞时的导航问题

GPS与INS融合算法，主要有卡尔曼滤波(KF)、粒子滤波(PF)等。

第二章 导航参考坐标系

• 2.1 坐标系变换
• 2.2导航常用坐标系
• 2.3坐标系转换

2.1 坐标系变换

在惯性导航计算中，经常需要从一个坐标系到另一个坐标系的矢量变换。

左乘旋转矩阵R: 其中R表示将向量r从k坐标系变换到m坐标系的矩阵。
（向量的上标表示其所在的坐标系，通常向量的上标会与矩阵下标抵消）
变换矩阵R的逆：描述了从m坐标系到k坐标系的变换；
如果两个坐标系是互相正交的，它们的变换矩阵也是正交的，此时矩阵的逆就等于它的转置。参考：正交矩阵与旋转矩阵的关系

• 反对称矩阵（Skew-Symmetric Matrix）
  对称矩阵：AT = A
  反对称矩阵：AT = -A
  两个向量在计算外积时，通常可将其中一个向量写成反对称矩阵：使用^（hat）符号表示
  外积：向量1x向量2——>矩阵1·向量2 的形式
  

2.2导航常用坐标系

(1) 地心惯性坐标系：Earth-Centered Inertial Frame（ECI 简称i系）

以地球质心为原点，不参与地球自转，OXi、OYi轴在赤道平面内正交并指向空间的两颗星，OZi轴平行与地球自转周并指向地球的北极。三个坐标轴指向惯性空间固定不动，这个坐标系是惯性仪表测量的参考标准。

(2) 地球坐标系：Earth-Centered Earth-Fixed Frame（ECEF 简称e系）

地球坐标系是指固联在地球上的坐标系，原点在地球的质心，它相对于惯性坐标系以地球自转角速度15.041088°/h旋转。OZe轴平行于地球自转轴并指向北极，OXe轴在赤道平面内指向格林尼治子午线，OYe在赤道平面内指向东经90°方向, OZe轴与OYe和OXe构成右手系。

(3) 地理坐标系：Local-Level Frame（LLF）

俗称东北天坐标系，原点与传感器重心重合，y轴指向正北c. x轴指向东， z轴穿过地心指向天。
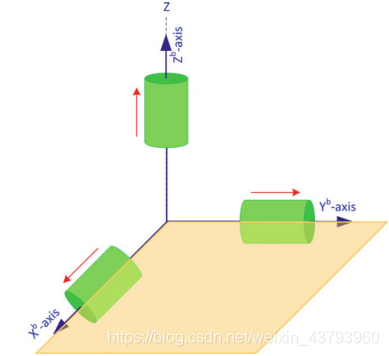
(4) 载体坐标系：Body Frame （b系）

在可移动的载体中，加速度计传感器的敏感轴与安装传感器的移动平台的轴重合。这些轴通常被称为body frame。
定义：原点与载体重心重合， y轴指向前方（横滚轴Roll）， z轴指向垂直向上，也被称为偏航轴（Yaw），x轴为俯仰轴（Pitch），xyz构成一个右手坐标系，可直观理解为“右前上”坐标系。


其中载体系相对于地理坐标系的欧拉角：Roll、Pitch、Yaw表示如上图。

2.3坐标系转换

将一个矢量从一个坐标系转换成另一个坐标系可以使用方向余弦、旋转(欧拉)角或四元数。它们都涉及一个旋转矩阵，称为变换矩阵或方向余弦矩阵(DCM)。在旋转矩阵的表示中，下标表示向量来源的坐标系，上标表示目标坐标系。例如： k系中的向量r变换到 l系中，可由下式表示：

欧拉角与旋转矩阵
坐标系a可通过旋转矩阵变为坐标系b，也可以通过对z，y，x轴逐步进行旋转得到。
如:绕z轴旋转 gama角度，可得到向量r1在a系与b系之间的旋转矩阵：

同理：
绕x轴的旋转

绕y轴的旋转

将三次旋转连续左乘（顺序 z，x，y），可以得到：

*对于小角度的旋转，有以下近似：

通过小角度近似，旋转矩阵可近似为：

第三章 GPS全球定位系统

• 3.1 GPS 观测
• • 3.1.1伪距测量
  • 3.1.2 载波相位测量
  • 3.1.3 多普勒测量
• 3.2 GPS信号
• 3.3 GPS误差源
• • 3.3.1 卫星时钟误差
  • • 3.3.2 接收机时钟误差
    • 3.3.3 电离层延时
    • 3.3.4 对流层延时*
    • 3.3.5 多路径误差
    • 3.3.6 卫星轨道误差
    • 3.3.7 接收机噪声
    • 3.3.8 用户等效距离误差
• 3.4 GPS的增强

三 GPS全球定位系统

全球定位系统(GPS)由美国国防部在20世纪70年代开发。GPS的定位基础是24颗卫星组成的网络。每颗卫星发送一个包含伪随机噪声(PRN)码与导航信息的无线电信号。接收机通过PRN码获得无线电信号的传输时间，传输时间乘以光速可初步计算卫星与接收机之间的距离(称为伪距离)。
根据导航信息计算卫星的位置。根据三颗卫星提供的信息，接收机通过三边测量法计算出自身的纬度、经度和高度；可根据第四颗卫星的信号来消除接收机的时钟偏差。

3.1 GPS 观测

GPS观测主要有伪距测量、载波相位测量和多普勒测量三种

3.1.1伪距测量

伪距是卫星和接收机之间距离的度量。
传输时间由导航消息计算，接收时间由接收信号(PRN码)与其接收方生成。伪距( p )的计算方法是取这些时间的差值，并将其与光速 c 相乘：

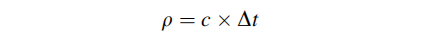
实际的伪距测量包含了很多干扰因素：

3.1.2 载波相位测量

接收机到卫星的距离也可以通过载波信号的相位来测量。
GPS接收机可以精确地测量一个周期的分相，但是从卫星到接收机的完整周期的总数最初是未知的。这称为整数模糊(IA)。IA解析后，通过将载波波长乘以完整周期(N)和小数部分，可以计算出距离，这个距离比PRN码计算出的距离精确得多。

考虑时钟偏移、大气延时、以及测量误差，可得到以下式子：

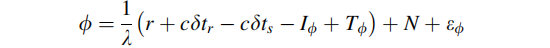
其中：
将上式与波长相乘，可将载波相位测量转换为米的单位：

3.1.3 多普勒测量

多普勒效应是由发射器和接收器的相对运动引起的电磁信号的频移。
基于这一现象，一些GPS接收机也通过测量接收信号的多普勒频率来计算用户的速度。
发射信号的多普勒频移( fd )、视线距离率( r )和波长之间的关系为：

3.2GPS信号

GPS最初以两个频率发送测距信号。
GPS卫星在两个无线电频率L1和L2（分别为1575.41和1227.60兆赫）传输信号。每个频率的测距码调制被称为伪随机噪声(PRN)序列或精确测距码。
单GPS接收器的精度约为5至30米。接收器必须确定卫星的位置，以便使用导航信息将距离测量值转换为用户的位置和速度。导航信息与PRN代码一起叠加在LI和L2载波上。该消息是二进制编码数据，包括关于卫星状态、星历(其位置和速度)、时钟偏差参数等信息。
美国政府正在不断提高GPS服务的性能，三个新的信号称为L2C, L5和LIC正在被引入民用。

3.3GPS误差源

GPS接收器使用三边测量原理，通过对至少四颗卫星进行距离测量来计算其位置。这些测距测量受到来自各种来源的误差的干扰。

3.3.1 卫星时钟误差

随着时间的推移，卫星时钟会偏离GPS系统的时间。
控制端根据监测站提供的卫星时钟数据观测数据，估算出卫星时钟的校正参数，并上传到卫星；卫星再将这些参数广播到导航信息中，使接收机在计算测量距离时对卫星时钟误差进行校正。

3.3.2 接收机时钟误差

为降低成本，接收机时钟比卫星时钟精度低得多，并带有偏差。
在使用三个卫星伪距估计当前位置时，如果可获得第四个卫星的伪距，那么接收机的时钟误差可进行同步估计，通常采用一个Kalman滤波器来实现。

3.3.3 电离层延时

电离层作为大气层的一部分，其中包含电离气体(自由电子和离子)，并占据地球表面约60至1000公里处的空间。这一层的电离水平随太阳活动而改变，影响电离层各层的折射率，从而改变GPS信号的传播时间
同时，卫星的高程也增加该误差的可变性，因为来自较低高程卫星的信号通过电离层的距离比来自较高高程卫星的信号更大。

伪距和载波相位的电离层延迟相等，但符号相反

其中f为载频，TEC为总电子数。TEC定义为沿电离层传输路径的1 m2横截面管中电子的数量，它在时间和空间上都是变化的。
同时配备了L1和L2的双频GPS接收机能够更准确地计算电离层延迟。

3.3.4 对流层延时*

对流层是地球表面8至40公里的大气部分，主要由干燥气体(N2和O2)和水蒸气组成。与电离层不同，对流层是电中性的，对于GPS频率来说是不分散的。但是由于存在折射，因此信号的传播速率相对于光速会衰减。L1和L2载波的对流层误差相同。
对流层延迟有干延迟和湿延迟之分。湿分量占对流层延迟的10%，由于水汽含量在局部范围内变化，因此很难建模。干分量模型更完善，占对流层延迟的90%。对流层延迟模型包括Saastamoinen模型、Hopfield模型和Chao模型。

3.3.5 多路径误差

多路径误差是城市环境中GPS信号的主要误差来源，GPS信号经过高楼建筑等物体表面，经过反射后到达接收机。间接到达的信号被延迟，并且信噪比很低。多路径误差可能导致位置误差超过10米。
载波相位测量的多径误差比伪距测量的误差低两个数量级。

3.3.6 卫星轨道误差

卫星在空间中的实际位置与接收机通过星厉数据计算的卫星位置之间的误差
控制端根据卫星先前的运动和地球引力来预测卫星轨道误差，并将该误差上传到卫星，作为星历数据广播给用户。因为星历模型是一条拟合实测轨道的曲线，它还包括相对于实际轨道的时变剩余误差。通常这个误差在2到5米之间。

3.3.7 接收机噪声

GPS接收机的随机测量噪声。
它是由天线电路、电缆、热噪声、射频信号干扰、信号量化和采样的累积效应引起的。

3.3.8 用户等效距离误差

在使用一些误差模型对测量值进行处理后，还存在一些剩余误差；将伪距测量的剩余误差结合起来，称为用户等效距离误差（UERE）。假设误差源可以分配到单个卫星伪距的，则这些误差是不相关的，那么一个卫星的综合UERE近似为一个零均值高斯随机变量：

3.4 GPS的增强

目前，一个独立GPS典型精度为：水平约为10米，垂直约为15米。这对于许多常用导航应用程序来说已经可以满足需求，但是对于一些重点应用项目来说还需要更高的精度，为了实现这一目标，需要使用各种其他系统来增强GPS。

为了达到更高精度的要求，可通各种增强系统：

• 增加额外的传感器: 该方法使用额外的传感器来补充GPS信息，提高整体的导航信息;例如：高度计、指南针、加速计、陀螺仪和里程计。
• 差分GPS的使用: 对于相对距离较近的用户来说GPS误差是相似的，这些误差被认为是空间和时间相关的。它们可以由一个位置已知的接收器来估计(基站/参考站)。估计的误差通过补偿算法传递给附近的GPS用户使用。这种技术被称为伪卫星差分GPS (DGPS)，
• 辅助GPS: GPS越来越多地被整合到手机中，手机需要额外的信息来及时提供位置信息。可以通过蜂窝网络辅助GPS (A-GPS)

第四章 惯性导航系统

惯性导航理论依据：
牛顿第一定律（在不受外力作用下，物体将保持静止或匀速直线运动）
牛顿第二定律（物体加速度的大小跟作用力成正比，跟物体的质量成反比；加速度的方向跟作用力的方向相同）

4.1 惯性导航系统的物理平台

平台式惯导：（下图a所示）惯性传感器安装在一组框架上（平衡环），通过扭矩电机根据陀螺仪感应的旋转来实现平台的旋转，使得平台始终与导航系保持一致。因此，加速度计的输出可以直接在导航系的速度与位置上进行积分。由于平台式惯导系统在机械构造上非常复杂并且价格昂贵，所以应用十分有限。

捷连式惯导：（图b所示）惯性传感器被刚性安装在移动平台的载体上，平衡环由计算机算法代替，通过坐标系变换算法来模拟平台的旋转。利用陀螺仪测量角速率来不断更新载体系和导航系之间的相对姿态。然后，加速度计的测量值通过旋转矩阵到导航系中，计算加速度。

由于捷连式惯导具备：可靠性、灵活性、低功耗、轻量、价低等优点，目前获得广泛用。

4.2 惯性测量单元IMU

INS主要由三个主要模块组成：惯性测量单元、预处理单元、机械化模块。
IMU使用3个相互正交的加速度计和陀螺仪：

4.3 惯性传感器的测量值

4.3.1静止状态下的加速度测量

当三轴加速度计静置于水平面平行时，此时加速度计测量的是地球重力加速度（其中包含一些误差与噪声），重力矢量垂直向下，与载体系的z轴重合，因此三轴的比力分别为：

若三轴加速度计的放置不与水平面平行，而是绕着x轴旋转，与地面形成一个角度p，如图所示：
此时z轴从原来的位置(虚线z)倾斜到一个新的位置z’。角度p被称为俯仰角。此时的yb、zb轴均可感知到重力矢量的分量，各轴比力为：


若再将传感器绕其y轴旋转，使其x轴与z轴偏移一个角度r，此时所有轴上都能测量到重力矢量分量：

4.3.2静止与运动状态下的角速度测量

假定当前载体系与ENU系（东北天）重合，三轴陀螺仪可以测量由于地球自转而产生的静止分量，也可以测量由于车辆行驶时经纬度的变化率而产生的非静止分量。

在静止条件下，陀螺在地球表面可以感知到地球的自转角速度We；此时陀螺仪各轴上的测量值取决于载体所在的纬度。由上图可知，Wx始终为0，当陀螺仪位于北极N时，Wz=We；当器件位于赤道时，Wy=We，当器件位于中间纬度 fai 时，满足以下公式：

所以，陀螺仪的静止分量可表示为：

在运动条件下，陀螺仪测量到的是载体各轴上的旋转角速度与地球自转角速度在各轴上的分量，以local-frame作为导航坐标系，假定物体向东北方向移动，则x轴（东向）上的角速度相当于移动物体在纬度上的移动速率：


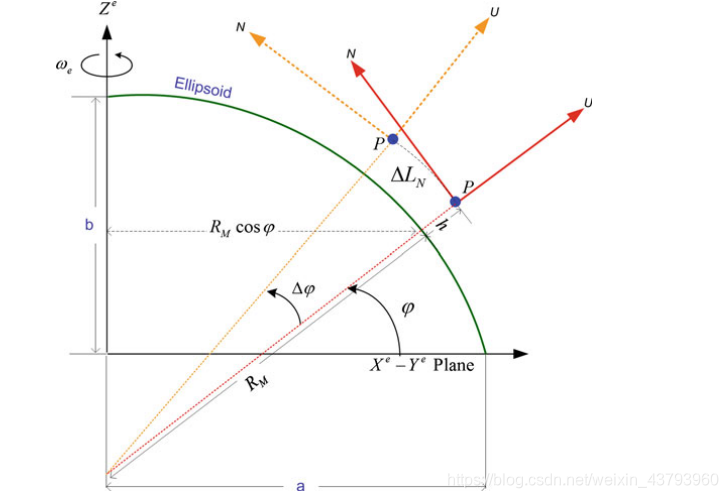
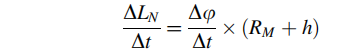
同理，东向的速度可表现为经度的变化率，继而可以表示为与地球自转轴重合的角速度（由于运动造成的），该角速度可被y与z轴的陀螺仪感知：



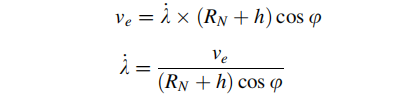
所以，陀螺仪的非静止分量可表示为：

4.4 惯性传感器误差

惯性传感器误差可分为两大类：系统误差与随机误差。

4.4.1 系统误差（可通过实验进行校正）

（1）系统偏置： 当无输入时，传感器自身存在的偏移量。

（2）尺度因子误差： 传感器应输出的实际值与输出值之间的比例关系。
尺度因子误差引起的加速度计输出误差与敏感轴上的真实比力成正比，同样陀螺输出误差与敏感轴的真实角速度成比例。

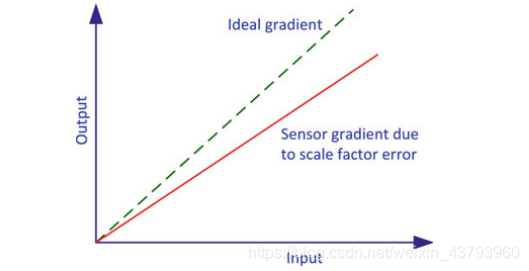
（3）非线性误差： 输入与输出之间的非线性关系。

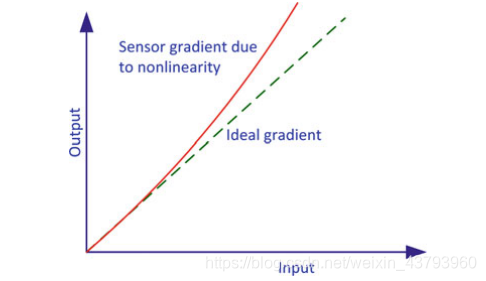
（4）尺度因子符号不对称： 正、负输入的尺度因子不同。

（5）死区： 有输入的情况下，输出为0的范围

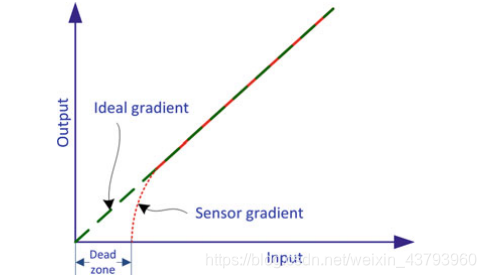
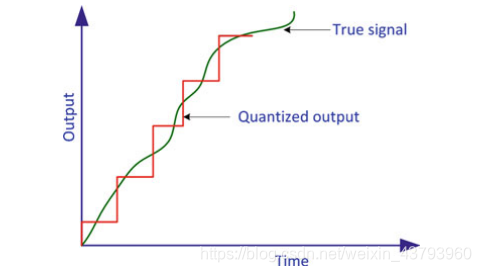
（6）量化误差： 将连续信号转化为离散信号是产生的误差。

4.4.2 随机误差

惯性传感器受到各种随机误差的影响，通常采用随机建模的方法来减轻这些误差的影响

（1）偏置漂移（Bias Drift）： 运行过程传感器偏置中随时间随机变化。称为偏差漂移。初始偏置是确定性的，而偏置漂移是随机的。偏置漂移的一个原因是温度的变化。

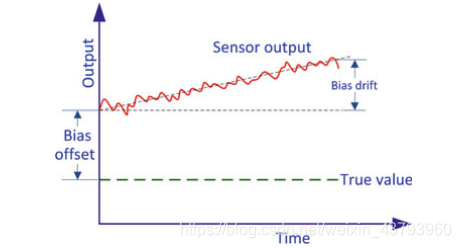
（2）高斯白噪声： 零均值的高斯白噪声

4.4.3 惯性传感器误差的数学模型：

（1）陀螺仪测量模型：
角速度的观测方程：


（2）加速度计测量模型：
加速度的观测方程：


4.4.4 惯性传感器误差的校正

• 六面法标定
  将x，y，z三个敏感轴依次朝上朝下静置，可计算得到bias和scale。

加速度计误差校正：



陀螺仪误差校正：
纬度为fai的载体系，若可感知到地球自转，则：

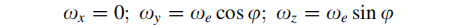
载体系中，指向天向的敏感轴，可以感知到地球自转的分量，并可以以此来计算校正参数：




对三个陀螺仪中的每个轴重复这个过程，以获得它各轴的偏差和比例因子。
低成本的陀螺仪无法探测到地球的自转速度,可以以恒定速率表60 °/ s旋转(或任何其他速率高于陀螺仪的检测阈值的转速)，替换方程中的 We sin(fai).

4.4.5 惯性传感器的初始对准：

传感器的加速度和转速进行一次积分，计算出速度和姿态，再对速度进行积分得到位置。导航方程需要获得位置、速度和姿态的初始值。这个过程叫做位置和速度的初始化以及姿态的校准。
*位置和速度初始化：
位置可以使用车辆开始移动前的最后一个已知位置进行初始化。对于INS与其他(通常是GPS)集成的系统，外部导航系统可以提供一个初始位置作为先验。
如果载体是静止的，那么速度可以初始化为零。如果载体是移动的，那么初始速度可以通过外部导航提供。

*姿态对齐：
两个步骤:首先，通过初始化俯仰（p）和横摇（r）角将载体系与"东北"对齐，再将航向角（y）与天向对齐。
当车辆静止时，加速度计的俯仰轴与滚转轴由于与地平面存在倾斜，因此可感知到重力矢量的分量。
在载体系静止的情况下，通过加速度测量的比力，可以计算出初始姿态角中的pitch和roll：
其过程如下：
已知local-frame下的重力矢量为：

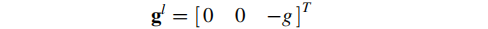
停止情况下加速度计测得的比力，可表示为“东北天”系下的重力矢量左乘旋转矩阵，即:从地理系变换到载体系下的结果：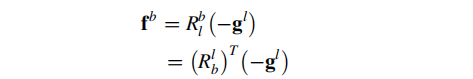
假定载体的俯仰（x：pitch）、横滚（y: roll）、航向（z: yaw）三轴上的姿态角分别为：p、r、y；旋转矩阵可以由下式表示：

将旋转矩阵代入得到：


由上式可知，通过静止时的加速度测量值感知重力矢量分量，可以得到与俯仰角（p）与横滚角（r）相关的方程，因此可以求出相应的姿态角：

而航向角（y）是无法通过坐标轴与水平面对齐的方法得到（因为改变航向角，重力矢量始终指向下不发生变化），要想求出航向角，还需要借助陀螺仪的测量。
若陀螺仪可以感知到地球自转，则：

在初始对准过程中，由于保持静止，后一项为0：

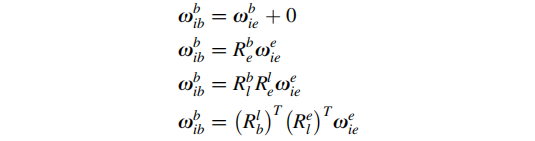
其中：


地球自转角速度We约为：15.04deg/h
代入以上式子，则载体系相对于惯性系的旋转角速度为：

因为p和r在上一步骤中已经通过加速度测量值求出，因次在该式中，可以将Wx乘以cos( r)，Wz乘以sin( r),得到：

因此：

求出航向角为：

相对于地平面，俯仰角与横滚角其实很小，可做以下近似：

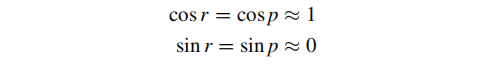
则航向角可简化为：

注意： 需要注意的是，使用陀螺仪感知地球自转来求航向角的方法只对较高精度的IMU可行，对于低精度的IMU，其噪声阈值超过了地球自转信号，因此无法探测到地球的自转。对于这些低精度的IMU，航向角的估计需要通过罗盘、磁力计、或者GPS获得。

第五章 惯性导航系统模型

• 5.1.INS Mechanization
• • 5.1.1 惯性系（i-frame）作为参考系
  • 5.1.2 地心地固坐标系（ECEF） 作为参考系
  • 5.1.3 当地水平坐标系（local-level frame）作为参考系

• 5.2. 旋转矩阵的参数化
• • 5.2.1求解旋转矩阵
  • 5.2.2求解四元数
  • 5.2.3 数值积分法求解
  • 5.2.4 旋转矩阵与四元数的相互转换
  • 5.2.5 旋转矩阵与欧拉角的相互转换
  • 5.2.6 旋转矩阵、欧拉角、四元数
• 5.3.当地坐标系（l-frame）的导航参数求解步骤

• 五 惯性导航系统模型

  两种建模方法：动力学建模（Dynamic Modeling）、运动学建模（Kinematic Modeling）

  动力学建模： 对力与相互作用引起的运动进行描述。表现一个物理系统对另一个物理系统的影响。例如：牛顿第二运动定律，表达了由力模型：F{r, v, t} 引起的运动变化。其中r是位置向量，v是速度向量，这些被称为状态向量，时间t是一个自变量。
  F{r, v, t} = ma= mv’= mr’’
  r( t) =r( t, b, c) 其中c，b为常数
  r( 0) =r( 0, b, c)
  v( 0) =v( 0, b, c)

  地球的自转和描述卫星绕地球运行的运动通常使用动力学建模。但不适用于物体在地球表面的运动。

  运动学建模：运动学建模常用于对运动物体进行动力学建模不切实际的情况。它研究的是物体的运动，而不考虑其质量或作用于其上的力，从而排除了力模型。在运动学建模中，物体的运动完全是根据位置、速度和加速度测量值来确定的，这些测量值统称为可观测值。
  根据可观测到的结果，位置矢量可表示为：r( t)={ x( t ) , y( t ) , z ( t ) }
  速度矢量为：
  
  加速度矢量为：
  

  5.1 INS Mechanization

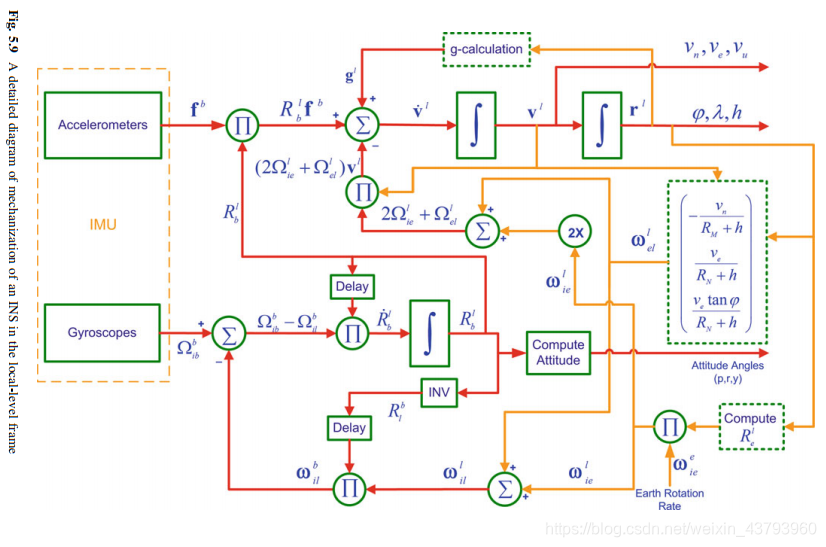
  Mechanization：是把IMU的输出转换成位置、速度和姿态信息的过程。IMU输出包括陀螺仪测量的三轴的旋转速率和加速度计测量的三轴加速度。系统框图如下所示：
  

  5.1.1 惯性系（i-frame）作为参考系

  
  加速度计的输出称为 比力f（除了重力以外的力）：
  
  其中，f为比力，a为载体测得的加速度，g为 重力矢量。
  测量值是在载体系（b）获得的，通常假定传感器的三轴与载体系重合，此时测量值可以通过3x3的旋转矩阵Rib变换到惯性系上（从b系变换到i系）：
  
  i系下的Mechanization方程可归结为：
  
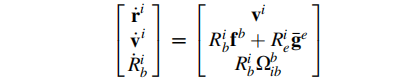
  ri =[ xi yi zi ] 是i系的三维位置矢量；vi =[ vxi vyi vzi ] 是i系的三维速度矢量
  Wib为陀螺仪输出的角速度，旋转矩阵的导数=旋转矩阵*角速度的反对称矩阵
  

  5.1.2 地心地固坐标系（ECEF） 作为参考系

  
  e系下的Mechanization方程可归结为：
  
  其中输入为加速度计测量的速度和陀螺仪测量的转速。输出是位置向量r，速度向量v和欧拉角，都在e坐标系中表示。

  5.1.3 当地水平坐标系（local-level frame）作为参考系

  local-level frame是最常用的坐标系，使用当地坐标系的优点：
  a. 当地坐标系可以直观地表现地球表面用户的导航状态。
  b. 由于I-frame的轴线与当地的东、北、天方向对齐，所以在当地坐标系中求解时，可以通过方程的输出处获得姿态角(俯仰、横滚和方位角)
  c. 水平(E-N)平面上导航参数的计算误差受舒勒效应的约束。
  d. 舒勒效应规定了水平面元件的惯性系统误差耦合产生舒勒回路，这些误差以舒勒频率的1/5,000 Hz振荡。
  
  

  5.2 旋转矩阵的参数化

  最常用的三种方法是欧拉角法、方向余弦法和四元数法。
  欧拉角只需要三个独立的参数。方向余弦（旋转矩阵）有9个参数，其中6个是独立的。这两种方法在计算上较为复杂，不适用于实时的计算，并且欧拉角容易产生奇异点。旋转矩阵的求解是不封闭的。因此，参数化转换矩阵最有效的方法是使用四元数方法。

  5.2.1求解旋转矩阵

  从b系到k系的旋转矩阵随时间的变化率表示为：
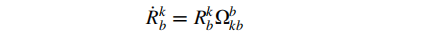
  其中，omga是传感器测量角速率[wx,wy,wz]的反对称矩阵：
  
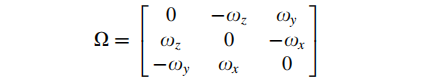
  求旋转矩阵的导数 需要求解9个微分方程，才能从角速度数据中得到变换矩阵。
  现在讨论这个方程的一个封闭解。假设角速度w在很小的时间间隔内是恒定的。则旋转角度的增量为：
  
  根据推导式，可以将旋转矩阵写成递归的形式：
  
  省略中间推导过程，最终得到以下结果：
  
  

  5.2.2求解四元数

  欧拉定理指出,刚体相对于参考系的旋转，可以表示刚体绕固定轴旋转一个角度。
  
  上图表示了一个角轴旋转，其中矢量n为旋转轴，theta为绕n旋转的角度。三个角 alpha、beta、gama定义了单位矢量旋转轴n的方向。
  四元数可通过角轴表述为：
  
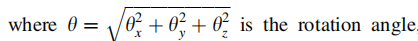
  四元数由一个实部与三个虚部构成，根据上式可知，四元数通过三个独立的分量便足以描述刚体的旋转，并且存在以下约束：
  
  四元数的导数为：
  
  
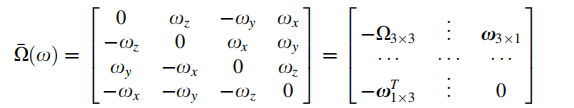
  将其表示为递推式：
  
  令：
  
  
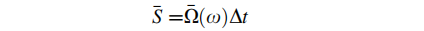
  则：
  

  5.2.3 数值积分法求解

  在旋转速率较低的情况下，可以采用数值积分的方法求解，即：
  
  
  相当于对递推结果进行一阶近似。

  5.2.4 旋转矩阵与四元数的相互转换

  若已知四元数 q=[ q1,q2,q3,q4],则可通过下式得到旋转矩阵：
  
  同样，在确定旋转矩阵后，也可将其转化为四元数（对准过程中测量的姿态角确定初始旋转矩阵后，计算四元数的初始值）：
  

  5.2.5 旋转矩阵与欧拉角的相互转换

  
  

  5.2.6 旋转矩阵、欧拉角、四元数

  四元数方法的优点：
  a. 四元数只需要求解4分方程（4个自由度），而旋转矩阵需要求解6个方程（6个自由度）。
  b. 四元数避免了使用欧拉角时可能出现的奇异性问题。欧拉角奇异性问题
  c. 四元数计算相对简单

  四元数方法的缺点：
  结果中存在非线性项以及需要在计算周期中重新正规化。

  以下罗列使用欧拉角、旋转矩阵、四元数三种方法对旋转进行参数化的优点和缺点：

  方法	优点	缺点
  欧拉角	3个自由度（仅需3个方程即可求解）、可直接求出Roll、Pitch、Yaw	非线性微分方程、角度正负90°时存在奇异性
  旋转矩阵	非奇异性、线性微分方程	6个自由度、计算复杂、无法直接求出欧拉角
  四元数	4个自由度、非奇异性、仅需要3个微分方程	无法直接求出欧拉角、初始化时需要借助欧拉角

  5.3 当地坐标系（l-frame）的导航参数求解步骤

  a.陀螺仪中获得的旋转速度(wx，wy ，wz)与加速度计测得的加速度（ fx，fy，fz）构成IMU输出。
  b.根据加表与陀螺仪计算俯仰，横摇和方位(p,r, A)的姿态角
  第四章中【通过加速度测量的比力，可以计算出初始姿态角中的pitch和roll，若角速率(wx，wy ，wz)可以感知地球自转则可以求得航向角】。由此得到b系相对于local系的旋转矩阵Rlb。
  c.使用前一步计算得到的Rlb，将b系中的比力转化为local系中的比力，得到东北天坐标系下的加速度为：(fe, fn, fu)。
  d.加速度计除了比力外，测量值中还包含地球引力与科氏力，因此需要除去这两个影响因素。
  e.通过对东北天坐标系下的加速度 (fe, fn, fu)进行积分，计算东、北、天的速度(Ve, Vn, Vu)。
  f.通过对东、北、天的速度(Ve, Vn, Vu)进行积分，计算 大地坐标系下的位置（纬度，经度，高度）。
  

  第六章 惯性导航误差建模

  6.1 导航误差状态方程（L系）

  INS的准确性受到各种因素的影响，如：初始对准过程中的误差、传感器误差、算法误差。
  若知道这些误差对导航参数(位置、速度和姿态)的影响，就可以通过建模来进行误差的估计，从而减小误差对导航结果的影响。
  因此，误差模型是分析和估计惯性导航系统误差源所必需的。估计器包括：卡尔曼滤波（KF) ；粒子滤波(PF) 和AI技术统上。
  Mechanizaion状态方程用于确定性动态系统物理过程的描述。这些方程的解中含有误差(确定性和随机性)，因此需要使用传感器误差模型来进行分析和估计。
  动态系统的的误差随时间变化，因此可以用微分方程来描述。由于这些方程是非线性的，在使用卡尔曼滤波之前需要将它们线性化。

  根据上一章可知，导航参数方程具有以下关系：
  
  LLF系（东北天）下的误差状态方程包括：纬度、经度、高度误差；东北天三个方向的速度误差、三个姿态角的误差；以及加速度计误差和陀螺仪漂移；
  总误差为15维的状态矢量：
  

  6.1.1导航误差——位置误差（L系）

  位置误差指的是，地理位置（纬度、经度、海拔）估计值的误差，已知位置的导数为：
  
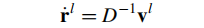
  位置误差定义为：
  
  通过一阶泰勒展开，整理等式右侧，并省略矩阵中的极小项，得到位置误差的导数具有以下形式：
  
  
  由上式可知，位置误差的状态方程与位置状态方程的转移关系近似相同。

  6.1.2导航误差——速度误差（L系）

  加速度测量值需要去除科氏力和重力矢量的影响后，才可进行积分计算。
  
  假定上式的误差可写成：
  
  则，速度误差为：
  
  将上式等号右边分为5个子项：

  (1)根据反对称矩阵定理：Ab=-Ba，第一项可改写为：
  
  其中：Fl为在L系上加速度比力矢量 fl:[ fe, fn, fu ] 的反对称矩阵；
  (2)第二项
  
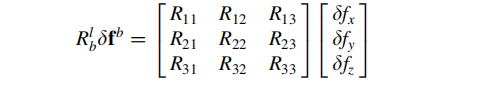
  (3)第三项
  由上一章已知，l系相对于e系的角速率、e系相对于i系的角速率为：
  
  将角速率矢量转化为反对成矩阵形式，并代入到第三项中，得到：
  
  (4)第四项
  角速率的误差定义：
  
  省略中间推导过程，可得到：
  
  代入定义：
  
  

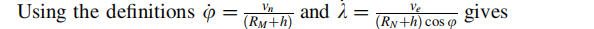
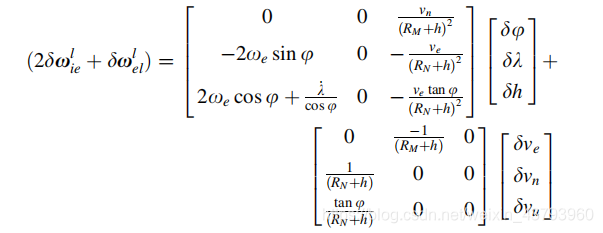
  省略分母的二次方项，得到：
  
  因此，第四项最后结果为：
  
  (5)第五项
  R为地球半径，g为重力矢量的模
  
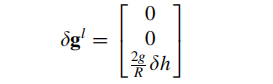
  经过整理合并，速度误差可写成：
  
  方程右边的第三项和第四项中，包含以地球半径作为分母的元素，以及乘以地球自转角速度（we）的元素，这些元素相对较小，在实际计算可忽略不计。因此，省略较小项的速度误差可简洁的表示为：
  
  注意：加速度分量fe 、fn与重力矢量相比是很小的(接近于零),而 fu 接近重力加速度(9.8米/ sec2)。
  因此，根据上述关系可知 deta( ve)与deta( r)、deta( vn)与deta( p)之间存在强耦合关系，而deta(ve)、deta(vn)与deta(A)之前是一种弱耦合的关系。

  6.1.3导航误差——姿态误差（L系）

  姿态误差：两个坐标系相对旋转的误差，实际上是由角速度误差引起的。
  根据上一章，已知旋转矩阵的状态方程：
  
  由于理论计算值存在误差，因此与真实值之间存在一个误差小量：（用带上三角的符号表示理论计算值，不带上三角的符号为真实值）
  
  其中，旋转误差小量可以写为【欧拉角误差的反对称矩阵】乘以【两个坐标系之间的真实旋转矩阵】的形式：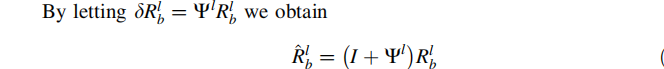
  
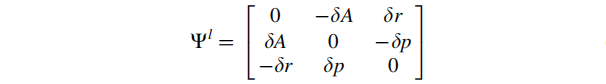
  将包含误差的式子代入旋转矩阵的状态方程：
  
  同时b系相对于l系的角速度的反对称矩阵也可写成：真实值角速度+线性角速度误差 的形式：
  
  这样就得到了一个旋转矩阵的导数与角速率误差、姿态角误差的关系式，为了进一步探究姿态角误差的变化与说明因素有关，我们可以通另一个方式获得一个等价的方程。

  为了得到矩阵R的变化率，需要对理论测量的旋转矩阵求导，用姿态角误差变化率表示变换矩阵R的变化率：
  
  
  通过两个等价方程，可以得到：
  
  消去等式两侧的相同元素：
  
  
  等式右边第二项为二阶误差，可以忽略不计，因此可以得到姿态角误差的变化率为：
  
  上式是反对称矩阵的形式，将其转化为矢量形式的姿态角误差变化率：
  
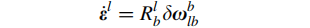
  上式说明了：姿态误差=[ deta( p) ,deta( r) ,deta( A) ]T 可通过角速度误差deta(Wlb)表示。

  下面分析角速度误差deta(Wlb)的表达式；
  载体系b相对于大地系l的 角速度Wlb 由l系相对于惯性系i的角速率（Wil） - 传感器测量的b系相对于i系的角速率（Wib） 得到，即：
  
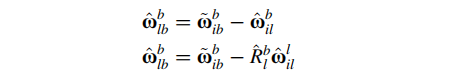
  角速度误差deta(Wlb)可表示为：
  
  根据反对称矩阵公式：Ab=-Ba ，有:
  
  将deta(Wlb)代入角速度误差方程：
  
  
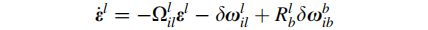
  根据上式，可知姿态角误差由以下几个因素构成：1. 导航参数误差 deta(Wil) ； 2.载体系旋转速率的测量误差 deta(Wib)；3. 以及i系相对于l系的角速率的反对称矩阵

  导航参数误差 deta(Wil)具有以下定义：
  
  
  

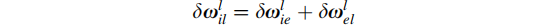
  同样，i系相对于l系的角速率的反对称矩阵
  
  
  
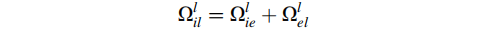
  综合以上式子，可以得到姿态角误差的变化率为：
  
  其中，第三项和第四项中包含地球半径的倒数项、以及地球旋转的乘积项，在大多数的导航计算中可以将其忽略不计，因此姿态角误差可以仅保留前两项，简化为：
  上式隐含的强耦关系也被称为舒勒效应。

  6.1.4 导航误差——传感器误差（L系）

  传感器误差主要是陀螺仪漂移和加速度计偏差，包含确定性误差与非确定性误差。确定性部分在实验校准过程中进行计算，并在测量中进行补偿。传感器误差的不确定性部分是随机的，采用随机模型进行建模。
  这些误差通常在时间上是相关的，常用的建模方法包括：随机游走过程、一阶高斯-马尔科夫（GM）过程和自回归（AR）过程。

  传感器的随机误差模型一般采用一阶GM过程进行建模，其一般形式为：
  
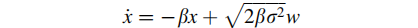
  x: 随机过程
  beta：过程相关时间的倒数
  W： 零均值不相关的高斯噪声的单位协方差
  segma2：随机过程高斯白噪声的协方差

  （1）加速度计Bias误差
  
  （2）陀螺仪漂移drift误差
  

  6.1.5 导航误差小结（L系）

  L系的位置、速度、姿态的状态误差以及传感器误差，可归结为：
  
  其中
  
  状态误差的流程框图：
  
  若将上述误差状态方程写为一阶微分形式：
  
  
  

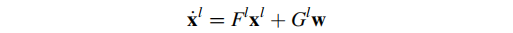
  6.2 Schuler 效应

  舒勒效应与速度误差deta(ve)与deta(vn)、俯仰角误差deta( p)与横滚角误差deta( r)在水平面上的耦合有关。这种耦合关系限制了水平和垂直速度以及俯仰和滚转角的误差。

  6.2.1 东向误差的舒勒效应

  根据误差模型，我们已知，横滚角roll误差的状态方程为：
  
  东向的速度误差Ve的状态方程为：
  
  因为 fu接近重力加速度g，而 fn 非常小，因次上式可进行简化，可知 deta（ve）与deta（r）之间存在强耦合的关系：
  
  对上式求导（东向速度误差求二阶导），并代入roll误差的导数关系式，可得：
  
  方程解得的 东向速度误差deta（ve）随时间振荡的频率非常小，等于1/5000 Hz。将这种小频率震荡称为 舒勒频率 fs，时间间隔为84.4分钟。因此，速度误差是有界的。
  舒勒频率：
  
  同理，若是对roll误差求二阶导，并代入东向速度误差的导数，得到：
  
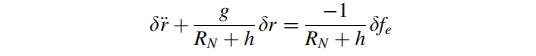
  方程解得到的横滚角误差deta（r）同样会随时间以舒勒频率振荡。因此，姿态误差会随着时间的推移而变得有界。

  东向速度误差deta（ve）与横滚角误差deta（r）之间存在强耦合关系，也就是说，如果从外部(如GPS)对INS的东向速度进行更新，从而得到准确的deta（ve）估计，也会使得横滚角误差deta（r）变得更准确。换句话说，速度的更新使得东向速度误差deta（ve）可观，而由于强耦合关系，这种可观性也会延伸到横滚角误差deta（r）上。
  

  6.2.2 北向误差的舒勒效应

  与东向的误差相似，舒勒效应 同样也体现在北向的误差模型上。
  根据姿态误差的状态方程，可知 俯仰角pitch的误差变化率为：
  
  而与之存在紧耦合关系的是北向的速度误差deta（vn）：
  
  简化为：
  
  分别对俯仰角pitch的误差和北向速度误差做二次微分：
  
  
  方程解得的俯仰角pitch的误差随时间以舒勒频率 fs 振荡；**北向的速度误差deta（vn）与俯仰角的误差deta（p）**之间的强耦合如图所示。
  
  当系统的北向速度由外部源更新时，不仅北向的速度误差deta（vn）得到了准确估计，由于强耦合关系，俯仰角的误差deta（p）也得到了准确估计。

  第七章 卡尔曼滤波

  导航系统的精度受到 惯性传感器初始化以及算法的误差影响。低成本MEMS传感器由于严重的随机误差，INS输出可能迅速漂移。因此低精度的IMU基本上不能作为导航独立传感器进行使用。
  在之前的章节中曾叙述过，对于水平面的速度与姿态角而言，若没有对速度进行持续的优化以消除速度误差，在长时间运动情况下会导致Vn和Ve值产生巨大的误差。同时，姿态角的误差，也需要依靠这些速度值来调节 ——【舒勒效应】。因此，建立精确的速度分量模型是十分重要的（可消除pitch、roll角的误差）。

  几类典型的测量更新方式：
  1）位置 或坐标更新——“CUPT”
  2）速度 或零速度更新——“ZUPT”
  3）姿态更新

  通过外部测量进行INS更新的方法有很多种：包括卡尔曼滤波(KF)、粒子滤波(PF)和人工智能(AI)。
  通常，将惯性导航系统与GPS辅助系统相结合，利用卡尔曼滤波对惯性传感器误差进行估计和补偿。总的来说，卡尔曼滤波器是一种从被噪声污染的测量值中最优估计系统状态误差的算法。这是一个顺序递归算法，提供了一个最佳的误差最小均方差估计。
  卡尔曼滤波的优秀之处在于，它使用了所有可用的测量数据，不论它们的精度高低，都可以通过对测量值增加合适的权重来估计当前系统状态。

  在惯性导航应用中，卡尔曼滤波用于互补配置，将具有不同噪声特性的同一信号的冗余测量值结合起来，最小化误差。惯导系统能提供良好的高频信息，但由于积分运算，惯导系统的误差随时间不断增大，使得加速度计和陀螺仪的偏置误差在输出端积累。惯性传感器的偏置误差通常出现在传感器输出的低频部分，称为长期误差。另一方面，许多其他导航系统(如GPS)具有良好的低频特性，但容易产生高频噪声。因此，利用KF可以从外部源的准确低频数据中获益，从而限制INS的长期误差。有许多外源可以为INS提供可靠的帮助，包括雷达、GPS、车轮传感器、激光测距和存储的图像数据库。
  在下文中将主要考虑全球定位系统作为外部源（由于GPS的准确性，全球可用性和低成本）。

  7.1 离散卡尔曼滤波

  卡尔曼滤波要求系统为线性的系统，离散时间的线性系统可描述为：
  
  其中：Wk-1为过程噪声。由于噪声对动态系统的影响表现在状态矢量的多个分量上，因此需要使用一个噪声分布矩阵G来表述噪声与各个状态分量之间的耦合性。

  系统的离散时间线性测量方程为：
  
  卡尔曼滤波基于以下假设：

  1.状态方程和测量方程均可用线性模型表示；
  2.系统噪声Wk以及测量噪声 为不相关的零均值高斯白噪声：
  
  
  其中，Qk和Rk是正定矩阵。在INS/GPS积分中，
  Qk表示与INS误差相关的系统噪声的协方差矩阵，
  Rk表示与GPS位置和速度更新相关的测量噪声协方差矩阵。

  3.系统初始状态向量xo是一个与过程和测量噪声都不相关的随机向量，因此：
  
  4.初始状态x0以及其协方差矩阵P0是已知的：
  

  7.2 卡尔曼滤波的流程

  KF是一种递归算法，通过状态反馈来估计系统的状态。
  如图所示，卡尔曼滤波分为两个环节:(1)预测 /状态更新; (2)校正 /测量更新。
  在预测阶段，将系统状态及其协方差从k -1时刻传播到k时刻；然后在校正阶段，使用测量值更新先前的估计，最终得到校正后的状态估计。
  

  7.2.1 预测与时间更新

  根据 k-1 时刻的信息估计 k 时刻的系统状态，称之为“先验估计”——Xk(-)，假定系统噪声为零均值，则 k 时刻的状态估计可写为：
  
  其中Xk-1(+)为上一时刻的最优估计。
  同时，卡尔曼滤波还将 上一时刻 k-1 的不确定度传递到下一时刻 k，不确定度通过误差协方差来表示 Pk(-)，也称为先验协方差矩阵：
  
  其中 Pk-1(+)为上一时刻的协方差矩阵的最优估计，由 Pk(-) 和过程噪声Qk得到。

  7.2.2 测量更新与校正

  在预测了状态的先验估计之后，当获得外部源的测量信息时，先验估计会得到更正。
  测量协方差为Rk，表示测量数据的不确定度。
  在测量更新环节中，最重要的一步为：计算卡尔曼增益的加权因子 K
  
  卡尔曼增益使KF在最优估计算法中脱颖而出。
  由方程可知，K既依赖于先验协方差Pk(-)，又依赖于测量噪声协方差Rk。如果测量噪声较大(Rk较大)，或者过程噪声较小(Pk(-)较小）时，那么K就会变得相对较小。反之，若过程噪声较大(Pk(-)加大)或测量值的噪声较小时(Rk 较小)，则K相对较大。
  当K较大时，测量值将被赋予更多的权重，当K较小时，预测值的权重就相对较大。

  当 tk 时刻得到一个新的测量值 Zk 时，将其与基于先验状态估计的预测测量值 HkXk(-) 进行比较。用K对二者误差进行加权，并更新状态向量的预测以生成最佳估计。因此，tk 时刻的状态估计值为：
  
  在更新完系统状态之后，还需对新估计值 Xk(+) 的不确定度进行更新：
  
  对于上式的协方差矩阵更新公式P. D. Joseph 认为，即便求得的卡尔曼增益K 具有细小误差，但传递到上式时依旧会产生能严重的问题。因此，他主张使用一种被称为约瑟夫式的方程的扩展形式：
  
  上式得到的后验协方差在数值上是稳定的，即使K的计算有误差也能得到正确的答案。此外，这种形式的后验误差协方差可以保证Pk(+)是半正定的，有助于避免发散。

  在大多数INS应用中，KF更新过程的频率低于预测。例如，通过卡尔曼滤波将GPS和INS集成的典型应用中，预测可能以100hz的频率进行，而更新以1hz的频率进行。下图显示了典型组合系统的预测和更的过程：
  
  离散KF算法的数据流图：
  
  时间更新与测量更新的方程归结如下：
  
  

  7.3 卡尔曼滤波 算法步骤

  KF由5个步骤组成，算法流程如图所示：
  
  具体步骤如下：

  1. 首先，初始化滤波器。这需要为过滤器提供其状态初始估计X0和初始估计中的不确定性P0。Po的估计是基于对初始状态估计的近似精度，通常设置为相对较高的值。同时还需要向滤波器提供系统噪声协方差矩阵Q和测量噪声协方差矩阵R的初始估计值。这些估计值是根据之前的系统经验估算出来的。
  2. 预测步骤的第一部分：计算状态转移矩阵，将初始状态从 k-1时刻传递到k时刻, 并表示为Xk(-).
  3. 预测步骤的第二部分：计算先验状态的协方差Pk。通过状态转移矩阵、上一时刻的协方差Pk-1、过程噪声协方差Qk-1，以及噪声分布矩阵Gk-1得到。需要注意的是，如果过程噪声较大，Pk就会增大，从而导致先验状态的置信度降低。
  4. 测量更新阶段的第一步：计算卡尔曼增益Kk。卡尔曼增益的值取决于先验误差协方差Pk(-)、过程噪声协方差Rk、观测方程中的Hk。Pk(-)越大，增益越大，Rk越大，增益越小。
  5. 测量更新阶段的第二步： 继完成预测的第二部分后，当接收到测量值时，先验状态k(-)就会被更新。这一步基于预测的测量值HkXk(-)与实际测量值的差值。根据这一差值进行状态估计的修正，当K较大时，这个差值的权重更大，并添加到先验估计值中，并更新为后验估计值Xk(+)。但当K较小时，从测量中获得的校正信息的权重较小，此时认为先验估计相对准确。
  6. 测量更新阶段的第三步：在修正状态估计之后，KF进一步将先验误差协方差Pk(-)更新为后验误差协方差Pk(+)，以表示后验估计的不确定度。
  7. 卡尔曼滤波进入下一时刻的状态估计与测量更新。

  7.4 非线性卡尔曼滤波

  线性系统是理想化的结果，严格地说，几乎所有的系统都是非线性的（甚至欧姆定律也只是在有限范围内的一个近似，它的线性在超过一定的电压阈值之后就会失效(Simon 2006)）。
  由于许多系统非常接近线性，通过对非线性系统进行线性化，可以将线性估计理论应用于非线性系统。在非线性的卡尔曼滤波中，通常将误差状态作为估计值，而不是以系统状态作为状态估计。在GPS/INS的组合导航中，误差状态是由INS状态和辅助源状态(GPS)之间的差值形成的。可用的方法有线性KF (LKF)和扩展卡尔曼滤波（EKF）。

  7.4.1 线性化kalman滤波

  对于某一个系统，在标准轨迹附近进行线性化的的方法，被称为线性化卡尔曼滤波（LKF）。此处的标准轨迹通常是已知的，例如，船或客机的航线是预先规划的。对于INS/GPS组合导航系统来说，惯导的输出通常被认为是标准轨迹。
  线性化卡尔曼滤波是一个开环结构，其滤波器估计的误差虽然对INS的输出进行校正，但是对INS系统却不构成反馈。
  

  7.4.2 扩展kalman滤波

  轨迹的真值是无法事先知道的，因此通常将轨迹最优估计的结果作为标准轨迹。
  当卡尔曼滤波使用先前最优估计的线性化轨迹，而非预定义的标准轨迹时，这种卡尔曼滤波被称为扩展卡尔曼滤波EKF。
  EKF对应于闭环的结构，其滤波器估计的误差将反馈到INS系统以矫正其输出：
  

  7.5 卡尔曼滤波发散控制

  对实际系统进行数学表示和线性化的简化过程会导致系统模型的不完善，从而导致KF的发散。这个问题在KF理论的一开始就被发现了，提出的散度控制技术包括在KF过程模型中加入虚拟噪声、Schmidt epsilon技术、有限记忆滤波和渐消记忆滤波。

  7.5.1 KF过程模型中添加虚拟噪声

  为了使一个真实系统的数学模型易于处理，必须进行许多简化和假设。此外,大多数系统是非线性的，在使用KF之前必须经过线性化，而这种线性化的方法相当于对系统模型又做了进一步的近似。
  这一系列不确定因素，可能会造成KF性能下降，甚至发散。
  针对这种情况，可以通过增加过程噪声协方差Q 或者 测量噪声协方差R的方式引入人工噪声。
  因此，在实际应用中，Q和R的参数设定一般是基于之前经验所得，并通过调整，以优化系统的性能。

  7.5.2 Schmidt Epsilon方法

  在KF中控制离散度的一种方法是为估计误差的协方差矩阵定义一个阈值，使它不低于某个值。在卡尔曼滤波运行过程中，协方差矩阵Pk(-)不断变小，卡尔曼增益K也不断减小，从公式中可以明显看出，当Pk(-)很小时，K趋近0，新的测量值将无法得到足够的权重，滤波器的输出将主要取决于预测值。这一现象被称为Kalman filter incest 。
  在协方差阈值化中，通过给计算得到的误差协方差矩阵Pk(-)加上一个符号为正的小量 ，就可以确保卡尔曼增益存在一个下界。这个小量值是根据经验确定：
  

  7.5.3 有限记忆滤波

  在kalman滤波中，最新的估计值Xk(+)是基于从起始时刻到 k 时刻的所有测量值。为了得到最优估计值，滤波器必须考虑到之前的所有测量值。
  但是，旧的数据有时不仅无法提供有效信息，反而会导致滤波器出现问题。
  因此，在渐消记忆滤波方法中仅使用最近的测量数据，旧的信息将被丢弃。
  例如，仅使用测量的最后100个样本进行滤波。

  7.5.4 渐消记忆滤波

  有时，一些系统模型只在有限时间内是有效的，在超过一定时限之后，系统模型会发生变化。
  针对这种情况，可以通过逐渐减小测量噪声的协方差R的方式，来丢弃旧的测量值，以限制其对最新估计值的影响。
  这一思想可以通过引入渐消因子来表示：
  
  其中a是一个正的常数。
  随着时间的推移，k变得更大，Rk逐渐减小，因此最近数据所占的权重更大。

  同样，将渐消因子a引入误差协方差的计算公式中，也可以起到同样的效果：
  
  其中a的选值>1。

  7.6 卡尔曼滤波例子

  7.6.1 简单导航系统

  考虑一个匀加速直线运动的物体。
  速度误差随时间的变化率等价于加速度误差，同样，位置误差随时间的变化率等于速度误差，这可以用以下式子表述：
  
  此外，加速度计误差模型采用一阶高斯马尔科夫过程：
  
  那么系统方程用矩阵的形式表示为：
  
  假设GPS的位置更新是连续可用的。通过比较辅助源(GPS)和惯导源(INS)的输出，得到了测量更新方程。因此，提供给卡尔曼滤波器的观测值z为：
  其中，误差np为GPS的测量噪声。
  将测量z用误差状态矢量x来表示：
  
  若将位置测量更新替换成速度测量更新，则：
  其中，误差nv为GPS的测量噪声。
  此时，z与误差状态矢量x的关系表示为：
  
  若对位置与速度同步更新，则：
  

  7.6.2 零速度更新

  对于无法获得连续更新的测量值的系统 或者在测量临时拒止的条件下，速度误差以及受到速度误差直接影响的姿态分量与位置分量都有可能不断增大。
  与单系统相比，使用ZUPT系统在惯性测量精度上有了显著的提高：
  ZUPT的具体步骤如下：

  1. 每2-4分钟停车30-60秒。
  2. 在停止时获得30—40个速度测量值。
  3. 将这些测量用于KF更新或速度曲线拟合。
     ZUPT的优点是不需要额外的设备，操作简单，成本低廉，预测和测量之间不存在同步问题。
     ZUPT的主要限制在于车辆必须立即停止，但这在实际运用中是无法实现的。

  7.6.2.1 通过ZUPT提高测量精度

  采用KF等最优估计方法来恢复ZUPT站间INS速度误差的行为。在这样的一个站点，INS输出速度与ZUPT沿三个相互正交的方向的速度之差被反馈给卡尔曼滤波器(如上图)。系统方程与更新测量的类型无关：
  
  其中x是15维的误差状态矢量：
  
  测量更新方程中的H矩阵取决测量值的可信度：
  
  其中：
  
  因此测量更新方程可写为：
  
  其中，Ve0,Vn0,Vu0为零速度更新
  下图例举了ZUPT各时间段内的速度与位置的变化趋势。可以明显地看出ZUPT可以防止位置误差不断增长。而在不使用ZUPT的情况下，位置误差会迅速累加，使得位置估计变得不可靠。
  
  ZUPT的性能受两个因素的影响：
  1.相邻两个ZUPT之间的持续时间。在这段时间里，速度误差随时间增长。因此ZUPT的间隔时间的选择直接关系到导航精度与性能。
  2.ZUPT时间间隔的选择，要使得KF算法收敛并校正INS误差。

  ZUPT的重要性包括以下几点：

  1. 限制了速度误差的增长，甚至可以将其重置为零。
  2. 有助于估计加速度计的偏置误差。
  3. 有助于估计三个姿态角的偏差。
     总的来说，ZUPT过程在限制测量误差长期增长方面是有效的。

  7.6.3 坐标更新

  在某些导航应用中，可以提供连续的坐标更新，或者是由坐标已精确预定义的CUPT站点提供。
  使用CUPT的过程中，物体运动将被临时中断，使得INS的输出可以与辅助源提供的测量坐标进行比较。
  在某些应用程序中，坐标更新可以连续提供，也可以在坐标已精确预定义的CUPT站点提供。如果导航系统作为一个独立的INS而不进行更新，我们预计长期的误差会显著增加，即使在使用高度精确的导航级惯性传感器的情况下也是如此。CUPT。物体的运动被中断，以允许INS的输出与辅助源提供的坐标测量进行比较

  7.6.3.1 通过CUPT提高测量精度

  CUPT整个过程类似于ZUPT，只是更新的是位置坐标而不是速度。其主要目的在于校正INS的位置误差：在每一CUPT时刻，INS输出的位置与CUPT间的差异将作为卡尔曼滤波器的输入，如下图所示：
  
  与ZUPT系统类似，CUPT系统方程与测量方程可以通过以下给出：
  
  
  
  
  

  第八章 INS/GPS组合导航

  对比INS与GPS导航方法，二者都有其各自的优缺点。
  惯性导航系统INS是一种全自主的导航系统，可以输出超过200Hz的高频信号，并且具有较高的短期测量精度。除了提供位置与速度之外还可以提供姿态信息。但由于算法内部存在积分，惯性传感器的误差会不断累积，使得长期导航误差无限制增长。
  与INS相反，GPS具有良好的长期精度，导航误差大致为几米，设备成本低于100美元。但是，它短期精度与输出频率较低。一个常规的GPS接收机通常无法提供姿态信息，除非采用一些额外的硬件或软件。此外，全球卫星导航系统需要依靠至少3颗卫星（4颗）的信号，而卫星信号通常会受到高层建筑、树木、隧道、大气以及多路径效应的干扰。
  从上述特点来看，INS与GPS具有较好的互补特性，将二者集成可以得到比单一导航系统稳定性更好、精度更高的导航方案。INS/GPS的组合导航系统可以输出高频率的导航参数信息（位置、速度、姿态），并且在长、短期的导航过程中均能具备较高精度。采用基于卡尔曼滤波的最优估计方法，对GPS和INS定位导航信息进行融合，可以得到可靠的导航解。GPS能够防止惯性数据漂移，INS能在GPS信号中断时提供位置、速度、姿态信息。
  典型的INS/GPS组合如图所示：
  
  滤波器可以采用传统的kalman滤波器、其衍生的LKF、EKF，或者其他滤波算法（粒子滤波）。
  滤波器通过比较惯导与GPS的输出，估计出惯导系统中位置，速度和姿态的误差，该误差对惯性输出进行校正。

  8.1 误差反馈

  基于状态误差卡尔曼滤波的INS/GPS组合导航系统，可采用两种误差反馈机制：开环和闭环。

  8.1.1 开环INS/GPS架构

  在开环结构中，位置校正、速度校正和姿态校正均在INS外部完成，其中估计误差在每次迭代时从INS解中减去。在这一过程中，误差与状态校正不会反馈给INS系统。
  
  开环结构的优点：
  在kalman滤波出现问题时，还可以通过原始的INS导航系统继续支持导航工作。
  但是，由于惯性漂移没有进行补偿，惯导误差随时间不断增大，使得线性假设失效。
  因此开环的结构更容易导致kalman滤波器性能下降。

  8.1.2 闭环INS/GPS架构

  在闭环结构中，KF估计的误差通过反馈的形式对INS进行校正。在误差估计反馈后，KF的位置、速度和姿态估计被重置为零。
  由下图以看出，kalman滤波估计的加速度计误差与陀螺仪误差在每个周期内都通过反馈以矫正IMU测量，继而作用于系统模型的计算。

  8.2 组合导航的类型

  为了最大限度地发挥GPS和INS的互补特性，提出了各种INS/GPS集成架构。
  可分为：松耦合、紧耦合和深耦合。

  8.2.1 松耦合 的INS/GPS组合导航

  
  在松耦合的结构中，GPS与INS均独立工作并各自提供导航参数的结果。为了提高导航精度，通常将GPS的位置与速度输入到滤波器中，同时，INS的位置、速度、姿态也作为滤波器的输入，滤波器通过比较二者的差值，建立误差模型以估计INS的误差。利用这些误差对惯导结果进行修正，得到速度、位置、姿态的组合导航结果。
  松耦合的结构框图 如上所示。
  松耦合的组合结构易于实现，并且比较稳定。当它为开环时，可以提供三个独立的导航结果(原始INS、原始GPS和组合结果)，当它为闭环时可以提供两个独立的导航结果（原始GPS、组合结果）。
  一个主要的缺点，当卫星数量低于最低数量时，GPS会暂时失效。并且GPS KF的输出是时间相关的，那么KF对于测量噪声不相关的假设就会受到影响，从而影响系统性能。

  8.2.2 紧耦合 的INS/GPS组合导航

  在紧耦合的导航系统中，GPS的伪距以及伪距速率的测量 将与INS预测的相应值 进行做差，并将差值反馈给kalman滤波器，用来估计惯导系统的误差。惯导系统的输出经过误差的校正之后，得到组合导航的解。
  紧耦合的系统结构如图所示。
  
  紧耦合的组合方式消除了松耦合方法中因卡尔曼滤波级联而产生的测量关联问题。除此之外，在卫星信号消失的情况下，紧耦合的组合模式依然能够提供GPS信号更新。
  由于紧耦合方法涉及对原始GPS数据的处理，因此在结构上相对于松耦合来说更加复杂。
  另一个局限在于，紧耦合结构无法得到独立的GPS导航结果。
  在INS/GPS组合导航使用相同硬件条件下，紧耦合的方式在精度与鲁棒性上均优于松耦合的结果。

  8.2.3 深度耦合的 INS/GPS组合导航

  
  深度耦合结构与紧耦合、松耦合主要存在两个区别：
  1.GPS接收机采用了回环校正的结构
  2.INS的信息作为GPS接收机的一个组成部分
  因此，在深耦合的结构中，INS与GPS将不再是独立的系统。
  该方案通常需要接入内部GPS硬件，实现起来比较复杂。
  深组合的优点是：这种方式降低了跟踪频率，提高了抗干扰能力。使得导航系统可以在较低的信噪比下工作，并且在卫星信号拒止的情况下GPS依然能够得到导航解。

  8.3 INS方程的动态误差模型

  在INS/GPS组合导航中，需要一个最优估计器来进行数据融合与估计。根据不同系统的需求，估计器的选择也有所不同。传统上，常用kalman滤波器进行惯性传感器的融合，因此，在后续主要针对这一组合进行研究。
  在导航坐标系的选择上，根据第(五)讲的内容，通常选用local-level坐标系（当地坐标系）来实现导航解算。第(六)讲分析了导航初始化误差、惯性传感器误差、算法误差等对惯性导航系统误差的影响。
  因此，此处要使用误差模型来分析和估计与INS相关的各种误差源，总结误差模型，以便于对组合导航的不同结构进行分析。

  在第6讲曾分析过，L系的状态误差矢量方程中，包含了沿大地曲面的误差（纬度误差、精度误差、海拔误差）、沿地球系的速度误差（东向速度误差Ve、北向速度误差Vn、天向速度误差Vu）、以及三个姿态角的误差（俯仰pitch、横滚roll、航向yaw）、同时还包括加速度计的bias和陀螺仪的drift。
  因此，完整的误差状态矢量表述为：
  
  
  （在L系下）上式中，各部分的误差线性化模型为：

  位置误差：
  速度误差：
  
  姿态误差：
  
  加速度误差：
  
  角速度误差：
  

  8.4 松耦合的INS/GPS组合导航模型

  8.4.1 系统模型

  连续时间卡尔曼滤波的系统模型：
  
  其中，G为噪声分布矢量，包含了与状态矢量相关的方差：
  
  F为动态协方差矩阵，包含了INS误差模型的各个部分【也就是之前的线性化模型】，可以总结为以下形式：
  
  状态矢量为 位置、速度、姿态、加速度计、陀螺仪的误差分量：
  

  因此，INS/GPS 松耦合组合导航的系统模型 可以写成：
  
  将上式进行展开，可以较为清楚地看到系统状态是如何通过动态矩阵进行耦合的：
  
  同理，离散时间的系统模型为：
  
  

  8.4.2 测量模型

  离散的KF测量模型表示为：
  
  其中，等式右侧第二项代表零均值的测量噪声，协方差为Rk。
  由于KF的状态矢量包含INS中的误差，因此对应的测量矢量由INS预测的速度、位置与GPS测量的位置、速度之差组成：
  
  Hk是tk时刻的测量矩阵，描述了在无噪声情况下通过状态变量的线性组合得到测量值Zk：
  
  那么，完整的松耦合测量模型可写为:
  
  将其展开得到：
  
  此外，还有两个重要的协方差矩阵Rk、Pk
  Rk包含测量状态对角线上的方差，定义为：
  
  预测状态的协方差Pk同样是一个对角矩阵，由对角线上的方差组成：
  
  其中，每一个对角元素的方差项也是3x3的对角矩阵，分别与位置，速度，姿态，陀螺仪偏差和加速度计偏差有关。

  8.4.3 INS/GPS松耦合总框图

  

  8.5 紧耦合的INS/GPS组合导航模型

  此处讨论紧耦合的组合导航模型。
  与第4部分类似，首先讨论从L系下的INS动态误差和测量模型；
  接着给出GPS误差和测量误差模型；
  最后通过kalman滤波实现综合系统模型与测量模型。

  8.5.1 系统模型

  INS part
  连续时间kalman滤波 INS系统模型（与松耦合相同）：
  
  FI：动态协方差矩阵
  G：噪声分布矩阵
  wI：白噪声

  GPS part
  kalman滤波GPS系统模型：
  
  状态矢量中包含：GPS接收机时钟误差和漂移，通过随机游走建模：
  
  动态协方差矩阵为：
  
  噪声分布矢量：
  
  各分量分别为：时钟偏差的白噪声标准差，时钟漂移的白噪声标准差
  因此，完整的系统模型可以表示为：
  

  结合INS与GPS的系统模型
  
  将 INS part 与 GPS part 的方程代入，得到上式的展开式：
  
  

  离散时间的系统模型：
  
  

  8.5.2 测量模型

  kalman滤波的测量模型在离散时间上的表达式为：
  
  对于紧耦合的系统来说，可用的观测数据为GPS的伪距以及伪距速率等测量值，因此，测量矢量即为INS估计值与GPS测量值之差：
  
  对于M个卫星来说，方程又可写为：
  

  伪距测量值【具体内容在第三章】
  
  GPS接收机获得第m个卫星的信号，可以通过以下模型来表示：
  
  
  利用卫星导航信息可以计算出卫星的钟差和电离层误差，对流层误差也可以通过建立适当的模型进行计算。因此，在对GPS误差进行校正之后，可以将校正后的伪距写成：
  
  等式右侧第三项为各种剩余误差。

  第m个卫星到GPS接收机的实际物理距离为：
  
  其中：
  则，伪距方程可重写为：
  
  其中：
  
  校正后的接收机位置定义为：
  
  其中：
  
  由于伪距测量方程是非线性的，因此在进行kalman滤波之前需要进行线性化（在xINS附近泰勒展开），对于函数 F(x,y,z)在线性化点（xi,yi.zi）的展开式为：
  
  将伪距方程在当前最优估计值（xINS, yINS, zINS）处线性化后，得到：
  
  由INS的输出定义的伪距测量为：
  
  因此，可以得到二者的差值：
  
  
  
  
  所以，伪距测量误差可归结为：
  
  对于M个可被观测的卫星，测量误差方程可表示为：
  
  对于ECEF大地坐标中的位置，需要使用以下关系将其转换成ECEF直角坐标：
  
  为了在kalman滤波中使用，上述方程组必须通过泰勒级数线性化：
  
  
  将上式代入到测量误差方程中，
  得到最终的伪距测量模型：
  
  伪距速率测量
  
  卫星和接收器运动产生的多普勒频移是二者相对速度在连线上的投影，与发射频率成正比，与光速成反比
  
  
  其中：
  
  根据多普勒测量，伪距速率可以通过下式进行计算：
  
  而实际的伪距速率为：
  建立伪距测量的模型：
  
  令接收机时间漂移：
  
  则
  由于我们想要得到的测量模型是关于deta（Vx）、deta（Vy）、deta（Vz）的函数，因此需要将上式转化为状态误差的形式。
  由INS测量得到的伪距速率为：
  
  其中，Vx,INS、Vy,INS、Vz,INS是INS在e坐标系下估计的接收机速率。
  将（8.66）与（8.67）式做差，得到：
  
  
  
  (8.70)中
  
  将（8.70）写成状态空间的形式：
  
  对于M个可被观测的卫星，伪距速率的测量误差方程可表示为：
  
  
  速度在L系与e系之间的关系可通过下式表示：
  
  代入R矩阵，得到：
  
  因此，伪距速率测量模型最终可写为：
  
  

  8.5.3 总体测量模型

  将5.2提供的伪距误差和伪距速率误差的测量模型结合起来，可以得到整体测量模型为：
  
  紧耦合集成实现的框图如图所示：
  

  第九章 三维简化的INS/GPS组合导航系统

  简化INS与GPS组合系统在三维路面上的导航

  这一章节讨论一种适用于任何轮式平台（含GPS）的航迹推算（DR）方法，该方法可消除使用传统IMU尤其是低精度IMU时产生的一些误差。
  1.首先分析讨论一个完整的INS系统，再概述用于处理误差源的理论方法。
  2.介绍了一种简化的惯性传感器系统，并与传统IMU进行比较。推导简化INS的机械化方程。
  3.接着，描述基于KF 的松耦合和紧耦合的简化惯性传感器系统与GPS的集成，包括线性化的系统模型和各种组合方案的测量模型。

  9.1 MEMS级IMU的三维定位的性能分析

  在GPS拒止的情况下，以低精度MEMS级IMU作为惯性传感器进行三维导航，三种未经补偿的bais如下：三个加速度计中未经补偿的bias；水平对齐的陀螺仪未经补偿的bias；竖直对齐的陀螺仪未经补偿的bias。
  正如第7章讨论的，LKF和EKF都试图通过传感器的误差模型对这些偏差进行补偿。在GPS可用时，误差模型间接得到更新。在GPS中断时KF滤波以预测模式运行，并从机械化解中减去INS误差的预测值进行修正。但这种补偿是不完善的，仍然存在一些未补偿的剩余误差。
  下面将讨论这些未补偿偏差的影响。

  第一个误差源，（第四章提到）当通过加速度计算位置与速度时，未经补偿的加速度偏差 bf 将会产生以下影响：
  1） 速度误差与时间 t成正比 （GPS拒止时，KF工作在预测模式下）
  
  2）位置误差与 t 的平方成正比
  
  第二个误差源，两个水平方向的陀螺仪之间存在一个未经补偿的偏差 bw ：
  1） 俯仰角或横摇角的误差与时间成正比
  
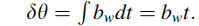
  这一小角度误差会造成INS无法正确对齐。当加速度从 b 系投影到 L系时，由于这一偏差的存在，会导致加速度矢量的投影产生误差。

  2） 加速度在水平方向上的误差（L系）
  
  在GPS拒止期间，deta（theta）为一个很小的角，通过近似 sin（deta theta）== data theta

  3） 偏差 bw将导致速度误差以及位置误差
  
  由上式，陀螺仪误差在位置上产生了三阶误差。当INS单独工作时，这些陀螺仪误差将是位置和速度误差中最具影响力的部分。

  误差的第三个来源：是由于垂直方向上未补偿的陀螺仪误差bw，会引起方位角的误差。
  
  同样，该方位角误差与时间成正比。

  9.2 解决MEMS级IMU在路面导航中存在的问题

  land-based vehicle :陆地车辆场景
  这一小节主要概述适用于(带有里程计或轮式编码器)陆地车辆的导航方法。通过一些方法来消除低精度IMU带来的未经补偿的误差，使得惯性传感器的成本最小化。
  为了解决上一节中提到的第一个误差（由加速度计偏差引起），可以将里程计的速度用到导航解算中。
  为了克服第二个误差（水平陀螺仪偏差），俯仰角与横滚角将综合加速度计与里程计的测量值得到。
  以下给出pitch角与roll角的简要推导方程：
  当车辆静止时，若俯仰和滚转轴所在平面与水平面之间存在倾斜，则加速度计测量可以在这两个轴上测量到重力分量。加速度计的测量值为：
  
  因为上式只使用了沿着 X 和 Y 方向的两个加速度计使，则，俯仰角和横摇角可以表示为：
  
  当车辆移动时，前向加速度计( y )(已修正传感器误差)测量车辆前向加速度以及重力分量。为了计算俯仰角，前向加速度计测量值必须减去里程计测量得的车辆加速度：
  
  其中，g为重力加速度，fy为前向加速度计测量值，aod为里程计测量的车辆加速度。

  与之类似，横向加速度( x )包含了车辆加速度的垂直分量以及重力分量。为了计算roll角，必须对加速度的垂直分量进行补偿：
  
  其中，fx为横向加速度测量值，vod为里程计测得的速度，wz为z轴上的陀螺仪测得的角速率。vod 与wz相乘即为车辆加速的垂直分量。

  对于低精度的MEMS IMU来说，通过两个加速度计来计算pitch和roll角 通常比使用两个陀螺仪在计算具有更大优势。
  原因1： 使用两个水平陀螺仪计算俯仰和横摇，涉及到积分操作，而使用加速度计算则不需要。积分的缺点在于，未经补偿的传感器误差通过积分累积，造成定位精度的不断下降。
  原因2： 陀螺仪与加速度计相比，加速计更便宜
  原因3： 垂直方向的陀螺仪的偏差需要用到组合导航的滤波器进行建模。

  9.3 三维简化的惯性传感器系统

  为了降低陆地车辆导航方案的成本，提出了一种简化的惯性传感器导航（reduced inertial sensor system，简称RISS）方法用于二维环境导航，其中采用单轴陀螺仪与里程作为传感器并通过kalman滤波与GPS集成。这种二维 RISS/GPS方法，需要假设车辆在水平面上移动。之所以被称为RISS，是因为它还包含一对用于计算俯仰角和横滚角的加速度计。
  一个单一的陀螺仪，其敏感轴与车辆的天向轴对齐。假定车辆在水平面上行驶，它的速度通过里程计的测量值计算得到，并与陀螺仪获得的航向信息一起使用，以确定东、北两个方向的速度，继而可以计算经度与纬度。这种简化的多传感器系统为2D路面导航提供了一个有效地方案。

  如前文中提到的，若要确定俯仰角和滚转角，可以使用两个额外的加速度计。这两个加速度计一个指向车辆的正前方，一个指向横向，再根据地球重力矢量以及速度测量模型，就可以计算出横滚与俯仰的角度。这些角度的计算是为了确定载体平面与水平面的关系，并不包含在KF的动态建模中。

  9.3.1 3D RISS概述

  此处主要讨论三维RISS解决方案，由两个用于计算俯仰和横摇的 加速度计 提供测量值被合并到一起以估计偏离水平面的运动，这种方法可以作为三维环境下的导航方案。

  事实证明，与完整的惯性传感器相比（完整的IMU包含了三个加速度计和三个陀螺仪），在陆地车辆上使用一个前向加速度计和三个陀螺仪的传感器配置，同样也能够进行导航参数的求解，计算出三维的位置、速度以及姿态。
  这也意味着三个陀螺仪加上从车辆里程计中获得的前向速度就足以实现三维导航。

  这一节介绍使用车辆的里程计、一个单轴陀螺仪和两个加速度计来实现三维导航方案。
  陀螺仪与车辆的垂直轴对齐，原本用于计算俯仰与横摇的两个陀螺仪在这里使用两个加速度计进行替代。三维RISS集成了垂直方向的陀螺仪和两个水平加速度计的测量数据，速度读数由里程表或车轮编码器提供，三维RISS系统如图所示：
  
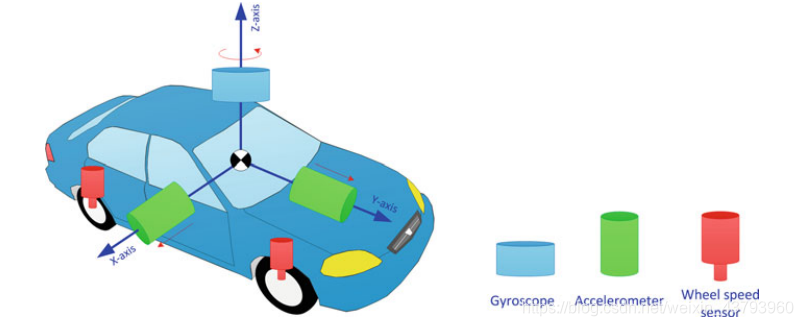
  利用三维RISS系统可获得三维位置、三维速度和三维姿态的导航解。

  9.3.2 （轮式车辆）采用3D RISS系统的优点

  三维RISS相对于二维航位推算的优点在于，使用两个加速度计的测量值 计算偏离水平面的运动。
  优点1：可以计算出正确的方位角。由于陀螺仪(与车身框架垂直对齐)在不完全水平状态下是倾斜的，因此无法测量水平E-N平面的角速度。由于方位角在E-N平面上，因此相比于2D车辆航迹推算时忽略水平面因素的做法，3D RISS方法通过检测和校正陀螺仪倾斜可以计算出一个更为精确的方位角。
  优点2：可以得到比2D RISS更精确的2D水平定位。 原因有二: (1)结合俯仰角和里程表中的速度可以计算出两个更为精确的水平速度，因此能够提供更好的位置估计; (2)方位角计算越精确，东向和北向的速度估计就越准确，继而得到更精确的位置。
  优点3：3D RISS 相比2D车辆航迹推算的优点在于可以计算出 向上的速度以及海拔高度。

  与传统IMU相比，3D RISS的优点是通过加速计来计算俯仰角和横滚角而非陀螺仪，在计算速度上使用了里程计而非加速度计。
  那么，为什么使用加速度计来计算角度比使用陀螺仪更好呢？优越性体现在哪里？
  解释：未经补偿的水平陀螺仪bias，会引起俯仰与横滚的角度误差，这一误差由于进行积分计算与时间成正比，会导致加速度矢量从boay系到 L系统的投影过程产生误差，引入一个加速度误差之后，后续计算的速度与 t2成正比，位置与 t3成正比。
  若是通过加速度计来计算俯仰和横滚角，可免去一次积分计算，并且角度误差不与时间t成比例。此外，角度误差引起的速度和位置误差也可以下降一个阶次。

  除了上述优点，RISS在速度计算上进一步优化。使用里程计来计算速度与使用加速度计计算速度相比，可以获得更好性能。
  解释：使用加速度计计算速度时，任何未经补偿的加速度误差都会引入一个与t成正比的速度误差以及与t2成正比的位置误差。在长期无法获得GPS信号的情况下，使用加速度计计算速度造成的误差随中断时间不断增大，这对导航计算来说是十分不利的。
  而使用里程计的测量值来计算速度可以避免一次积分计算，这意味只要进行一次积分就能够得到位置。

  在3D RISS中，唯一剩下的主要误差源就是 垂直对齐的陀螺引起的方位角误差，陀螺仪未经补偿的bias会导致方位角误差并与时间成正比。方位角引起的位置误差将正比于车速、时间以及方位角误差。这些误差必须在积分滤波器内通过模拟陀螺仪的随机漂移来解决。

  为了证明3D RISS比完整的IMU传感器在陆地车辆导航上更具优势，以下分别将两种导航方法用于路面汽车行驶的导航中，在约96公里的轨道上运行，持续时间约100分钟，得到两者的位置输出，两个系统的定位结果见图：
  
  图9.2为使用3D RISS系统得到的位置轨迹与高精度参考轨迹的对比。
  
  图9.3为使用IMU传感器估计的位置轨迹与高精度参考轨迹的对比。从图中可以看出，随着时间推移，Full IMU轨迹很快出现了漂移，并偏离真实轨迹。
  
  图9.4为运动起始位置的局部图，此处展示了使用full IMU更容易产生漂移。其中，3D RISS与full IMU中使用的MEMS传感器来自于相同的IMU（IMU300CC-100型），该IMU的陀螺仪bias为2°/s。

  9.3.3 3D RISS的运动方程推导

  本节给出了包含位置、速度和姿态状的三维RISS的非线性运动模型。
  使用通用的参考系，b系的x轴与车体的横向重合，y轴与车体的前向重合z轴沿着车体垂直向上的方向。局部坐标系（L系）是沿东、北、天方向的ENU坐标系。在k-1时刻时，旋转矩阵从车载体坐标旋转到局部坐标系为:
  
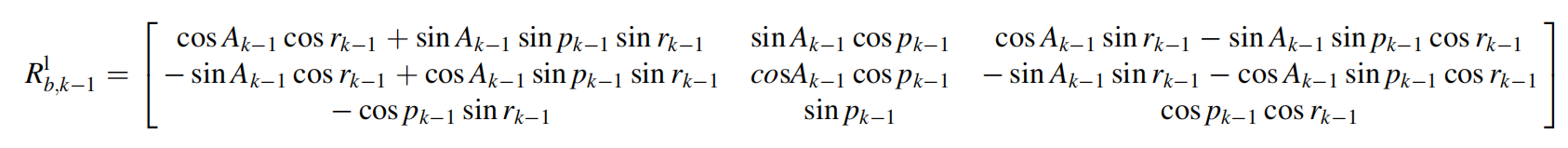
  为了描述运动模型，首先需要控制输入。由一个陀螺仪、两个加速计和里程计提供的传感器测量值组成了控制输入向量：
  
  
  定义系统的导航状态为：
  
  
  此处状态向量只包含了前向速度，在有些方程中采用
  
  将东、北、天的速度都作为状态向量。

  9.3.3.1 Pitch和roll角的计算

  对于陆地车辆来说，俯仰角是相对于水平地面的角度(即绕横向轴的旋转)，横滚角是绕纵向轴的旋转，如图所示：
  
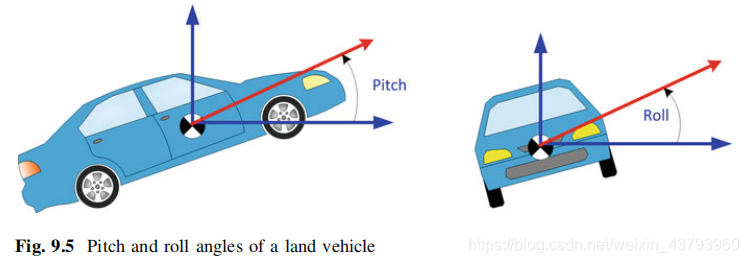
  当车辆运动时，前向加速度计测量车辆的前向加速度以及重力分量。为了计算俯仰角，需要在前向加速度的测量值中减去里程计测得的车辆加速度：
  
  同样的，横向加速度计测量车辆的横向加速度以及重力分量。为了计算roll角，必须对横向加速度进行补偿：
  

  9.3.3.2 航向角计算

  陆地车辆的方位角实际为车辆正前方朝向与大地北向的夹角，如图所示：
  
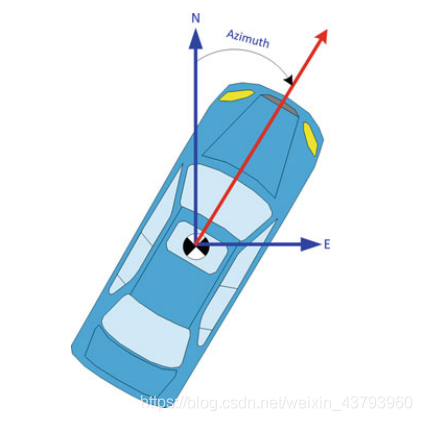
  在k-1与k的时间间隔内，绕载体b系的z轴逆时针旋转，得到：
  
  计算目标：求得方位角在E-N平面上的投影。
  在k时刻获得车辆b系下的前向单位矢量：
  
  假设在已知k-1时刻的车辆状态，对k时刻的车辆前向单位矢量进行估计：
  
  从k-1时刻的车辆载体坐标系到k时刻载体坐标系之间的旋转矩阵是Rz，那么两个单位矢量的关系可以看成：
  
  由于Rz是一个正交的旋转矩阵，因此：
  
  （注：正交矩阵性质：ATA=E 、AT=A’）

  由式可得，k时刻沿车辆前进方向的单位矢量，可由k-1时刻的车辆在 L系下的前向单位矢量得到：
  
  因此，由于绕z轴的旋转产生的新的航向角为：
  
  其中：
  
  使用上式定义的航向角，是相对于北向的夹角，沿顺时针方向为正。

  除了表现为车辆的旋转之外，方位角还有两个额外的分量。这是由于地球自转以及L系方向变化引起的。
  ··由于地球自转引起的分量为：
  
  We为地球旋转速率，这一部分可以直接在新的航向角上进行补偿。
  ··由于L坐标系相对于地球坐标系的方向变化引起的分量为（沿逆时针方向）：
  
  由于，车辆的body系与local-level系之间的关系为：
  
  代入（9.16）式，得到：
  
  在计算方位角时需要加上这一项。

  综上，得到最终的方位角计算模型为：
  

  9.3.3.3 三维位置、速度计算

  注：【非完整约束】非完整约束与完整约束的区别
  至少包含一个不可积微分约束的动力系统称非完整系统。对非完整系统，要用更复杂的微分方程来描述。带有滚动轮子的系统(如自行车、汽车、飞机起落架等)大都是非完整系统。位置约束为完整约束，速度约束为非完整约束。

  由于陆地车辆的非完整约束(non-holonomic constraint)，车身body系中的速度仅由车辆前向（纵向）速度构成，水平横向以及垂直向的速度分量均为0。
  因此，纬度可以表示为：
  
  其中，RM为地球曲率半径，deta( t)为采样时间。
  同理，经度可以表示为:
  
  海拔高度表示为：
  
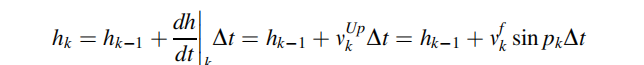
  其中，车辆前向速度为：
  

  3.4 3D RISS 运动模型概述

  完整的运动模型如下：
  
  如果在导航状态矢量中使用是L系中的速度分量，而非前向速度，那么运动模型将变为：
  
  三维RISS模型如图所示：
  

  4 KF用于松耦合的3D RISS/GPS集成

  非线性运动模型构成了机械化方程的基础，由此推导出的线性化误差状态模型，可作为kalman滤波的系统模型。
  为了简化线性化系统模型，并将其作为3D RISS的误差模型，这里做了两个近似：第一个近似，将俯仰和横滚角的误差作为状态量排除在积分滤波器之外。（正如前面所讨论的，俯仰和横滚的误差不随时间增长）第二个近似，假设陀螺仪(沿着车身b系的垂直向上方向)与位置L系的天向对齐，简化了方位角的计算。（由于这个陀螺仪的测量包含了地球自转的分量以及局地坐标系在地球系上的旋转，所以在积分之前这些量被从测量中除去。）
  基于上述方位角的二维近似，可以将L系中的方位角直接表示为：
  
  松耦合的3D RISS/GPS集成的系统框图如下所示：
  

  9.4.1 3D RISS的线性化误差模型

  3D RISS KF的误差状态系统模型可表示为:
  
  
  kalman滤波器的误差状态矢量为：
  
  其中：
  
  如先秦所述，运动模型时非线性的，因此必须对其进行线性化才能得到可作为KF系统模型的误差模型。
  通过泰勒级数展开并忽略高阶项，将方程线性化。
  得到对应的线性化误差状态系统模型为：
  
  其中：
  
  
  陀螺仪的随机误差以及里程计得到的速度，都采用高斯-马尔科夫模型。

  9.4.2 用于更新3D RISS的测量模型

  由于考虑的是松耦合集成，所以在KF的更新阶段使用了GPS的位置和速度进行更新，滤波器使用的测量模型为：（测量模型为RISS提供的3D位置、速度与GPS测量值的差值）
  

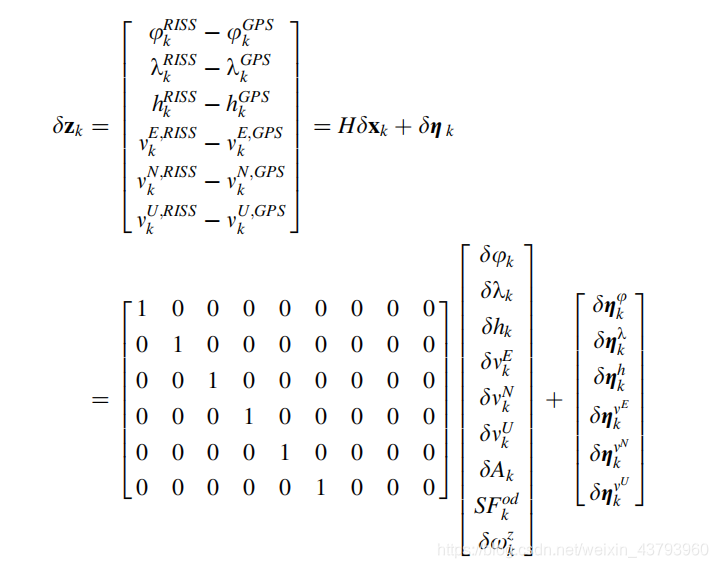
  9.5 KF用于紧耦合的3D RISS/GPS集成

  紧耦合的3D RISS/GPS集成系统框图，如下所示：
  

  9.5.1 系统模型的扩维

  紧耦合的系统模型与松耦合类似，在系统模型和状态矢量都包含了GPS接收机的时钟偏差以及漂移误差。因此RISS和GPS可以简单地结合在一起，得到以下完整的系统模型为：
  
  kalman滤波系统模型中的GPS方程为：
  
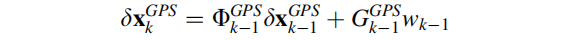
  GPS接收器的时钟偏差和它的漂移被包含在状态中，这些状态的系统模型是：
  
  
  因此，扩维后的状态矢量为：
  

  9.5.2 用于更新3D RISS的原始GPS测量模型

  给出紧耦合的KF线性化测量模型：
  
  
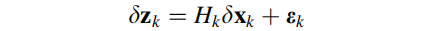
  GPS的观测值是伪距以及伪距速率。因此，对于KF的误差状态来说，测量矢量由 RISS 与 GPS的伪距测量值以及伪距速率测量值的差值构成：
  
  
  在第三章中提到过，GPS的测量值经过了时钟误差以及电离层和对流层的校正。对于M个可接受信号的卫星，以上方程可写为：
  
  这些非线性伪距误差来自于伪距测量值以及RISS计算的位置预测出的伪距值。
  因此，第M颗卫星与GPS之间的伪距可由以下模型表示：
  
  
  由RISS导航系统输出的预测伪距 定义为：
  
  其中，r(RISS,K)为车辆位置，由ECEF大地坐标系转换到ECEF直角坐标系，再由机械化方程计算位置输出得到。

  GPS伪距测量值与车辆位置无关，但对最新估计状态进行泰勒展开之后，使得RISS估计值与GPS测量值之间的差异可以被建模为与位置误差线性相关的式子：
  
  
  以分量形式表示：
  
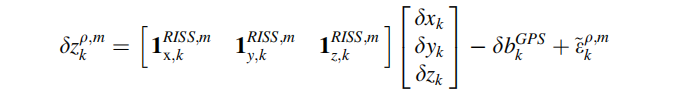
  其中：
  
  在获得M个卫星的测量之后，可以得到：
  
  其中：
  
  由于状态矢量的位置分量在大地坐标系中，因此需要将其转化到对应的直角坐标系上：
  
  上式的线性化位置误差为：
  
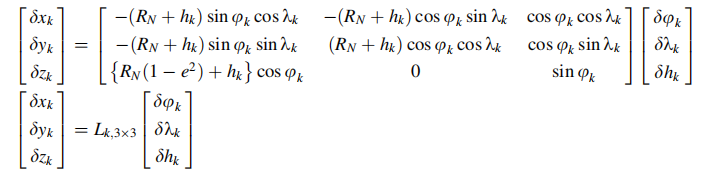
  将上式带入到（9.42）式中，得到：
  
  通过定义一个H矩阵，线性化的伪距测量模型为：
  
  通过测量卫星载频的多普勒频移，计算了第m颗卫星的伪距离速率测量值。如第3章所述，伪距离速率可视为接收器和卫星之间的相对速度测量，测量的方向是从卫星指向接收器方向的单位矢量，测量模型可以用数学形式表示：
  
  
  在（9.48）中：
  
  因此，可重写为：
  
  通过RISS估计伪距速速率为：
  
  其中 v(RISS,k)为通过RISS估计的ECEF直角坐标系下的车辆速度。
  因此，线性化的伪距速率测量方程如下：
  
  其中：
  
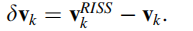
  对M个可接收信号的卫星，伪距速率测量可以写为：
  
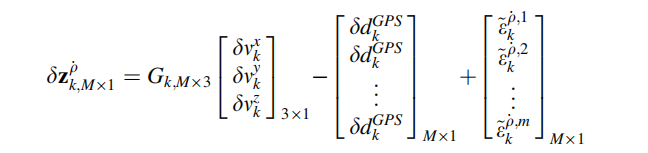
  速度在局部水平坐标系(L)与ECEF坐标系之间的关系为：
  
  
  将坐标系转换代入测量方程，得到伪距速率测量模型：
  
  其中：
  
  综上，得到包含伪距以及伪距速率的完整的测量模型为：
  

  参考文献：（转载）

  1.https://blog.csdn.net/weixin_43793960/article/details/105553608
  2.https://blog.csdn.net/weixin_43793960/article/details/105580707
  3.https://blog.csdn.net/weixin_43793960/article/details/105637849
  4.https://blog.csdn.net/weixin_43793960/article/details/105666006
  5.https://blog.csdn.net/weixin_43793960/article/details/105702657
  6.https://blog.csdn.net/weixin_43793960/article/details/105752280
  7.https://blog.csdn.net/weixin_43793960/article/details/105821655
  8.https://blog.csdn.net/weixin_43793960/article/details/106050193
  9.https://blog.csdn.net/weixin_43793960/article/details/106142967