数据结构Ｃ＋＋语言描述专题系列 （四） 链式栈和队列

1、指针与链表

一、指针

指针是一种数据类型，具有指针类型的变量称为指针变量。但事实上，可以将指针直接看成一种特殊的变量。首先，它与一般变量一样具有变量的三个基本要素：名字、类型和值，不同点主要在于类型和值上，指针命名与一般变量命名一样，都用标识符。

指针所存放的是某个变量的地址值，或者说它所表示的数据值是某个变量在内存中的地址值。通常所说的指针存放哪个变量的地址值，它就指向那个变量。

指针的类型是它所指向变量的类型，而不是指针本身数据值的类型，因为任何指针它本身数据值的类型都是unsigned long int型。

空指针 NULL
当前不指向具体的对象，不同的系统会使编译取不同的NULL值。在PC中的BC或VC，都取值0。如果考虑到移植，不要养成把NULL当成为0的习惯。

二、链式结构

每一个结点的地址存放在它前面的结点的指针域中。

结点的定义
struct Node {
//  data members
   Node_entry entry;
   Node *next;
//  constructors
   Node( );
   Node(Node_entry item, Node *add_on = NULL);
};

结点的构造函数(Constructors)
Node ∷Node( )
{
   next = NULL;
}
Node ∷Node( Node_entry item, Node *add_on)
{
   entry = item;
   next = add_on;
}

在使用中,第二个构造函数的第二个参数可以按缺省处理，即可作为NULL。也就是说第二个构造函数有2种方法引用，2个参数或1个参数。第二种情况下，第二个参数取缺省值NULL。

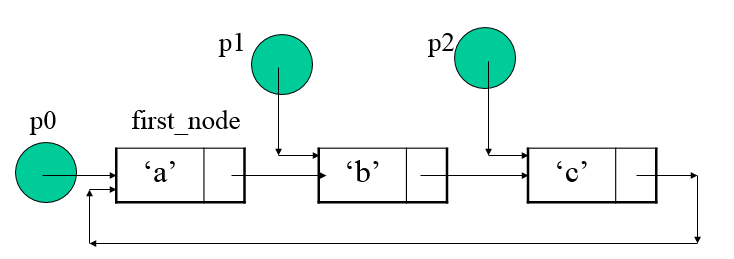
例
Node first_node(‘a’);
Node *p0 = &first_node;
Node *p1 = new Node(‘b’);
p0－>next = p1;
Node *p2 = new Node(‘c’, p0);
p1－>next = p2;

2、链式栈

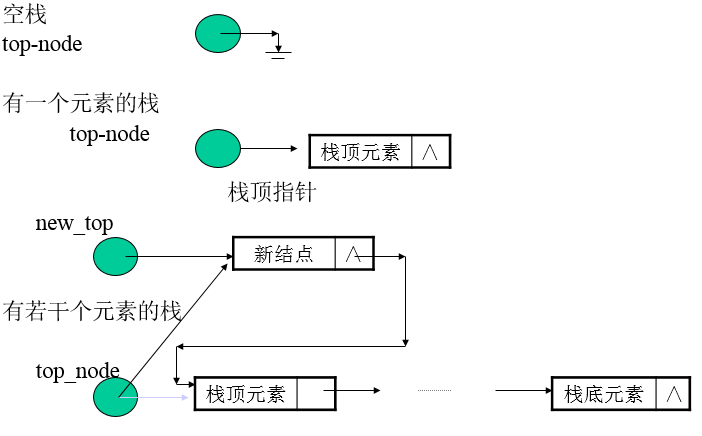
如何实现链式栈
链式栈的组织形式

与顺序存储的栈区别

链式栈类说明

class Stack{
public:
    Stack( );
    bool empty( ) const;
    Error_code push(const Stack_entry &item);
    Error_code pop( );
    Error_code top(Stack_entry &item) const;
protected:
    Node *top_node;
};

链式栈的图示

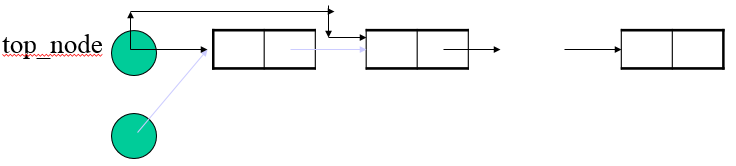
链式栈的入栈运算

Error_code Stack ∷push(const Stack_entry &item)
/* Post: Stack_entry item is added to the top of the Stack; returns success or returns a code of overflow if dynamic menory is exhausted */
{
   Node *new_top = new Node(item, top_node);
   if(new_top = = NULL) return overflow;
   top_node = new_top;
   return success;
}

链式栈的出栈运算

Error_code Stack ∷pop( )
/* Post: The top of the Stack is removed. If the Stack is empty the method returns underflow; otherwise it returns success */
{
   Node *old_top = top_node;
   if(top_node = = NULL) return underflow;
   top_node = old_top － >next;
   delete old_top;
   return success;
}

关于链式栈运算的副作用问题

例 一、 for(int i= 1; i<1000000; i + +)
               {
                   Stack small;     
                   small.push(some.data); 
               }

每次迭代产生一个stack对象，数据加入到相应的存储空间。因为动态生成，前次存储的数据会成为碎片，积累到一定程度引起系统崩溃。引入析构函数(destructor)。

Stack ∷～Stack( )
/* Post: The Stack is cleared. */
{
    while (!empty( ))  pop( );
}

产生垃圾(garbage)

例二、Stack outer_stack;
             for (int i = 0; i<1000000; i + +) {
                 Stack inner_stack;
                 inner_stack.push(some_data);
                 inner_stack = outer_stack;
              }
例三、
void destroy_the_stack (Stack copy)
{
}
int main( )
{
     Stack vital_data;
     destroy_the_stack(vital_data);
}

链式栈改进方法
赋值重载

void Stack:: operator = (const Stack &original) // Overload assignment
/* Post: The Stack is reset as a copy of Stack original. */
{
   Node *new_top, *new_copy, *original_node = original.top_node;
   if (original_node = = NULL) new_top = NULL;
     else {                   // Duplicate the linked nodes
       new_copy = new_top = new Node(original_node − >entry);
       while (original_node −>next != NULL) {
           original_node = originaLnode − >next;
           new_copy − >next = new Node(original_node − >entry);
           new_copy = new_copy − >next;
        }
   }
   while (! empty( ))         // Clean out old Stack entries
       pop( );
   top_node = new_top;     // and replace them with new entries.
}

拷贝方法的改进

Stack:: Stack(const Stack &original)      // copy constructor
/* Post: The Stack is initialized as a copy of Stack original. */
{
    Node *new_copy, *original_node = original.top_node;
    if (original_node = = NULL)  top_node = NULL;
    else {                   // 复制链式栈的结点
       top_node = new_copy = new Node(original_node − >entry);
       while (original_node − >next ! = NULL) {
            original_node = original_node − >next;
            new_copy − >next = new Node(original_node − >entry);
            new_copy = new_copy − >next;
       }
     }
}

修改后的链式栈说明

class Stack {
public:
//   标准的栈方法
   Stack( );
   bool empty( ) const;
   Error_code push(const Stack_entry &item);
   Error_code pop( );
   Error_code top(Stack_entry &item) const;
//  关于链式栈的安全的特殊方法
   ~ Stack( );
   Stack(const Stack &original);
   void operator = (const Stack &original);
protected:
    Node *top_node;
};

3、链式队列

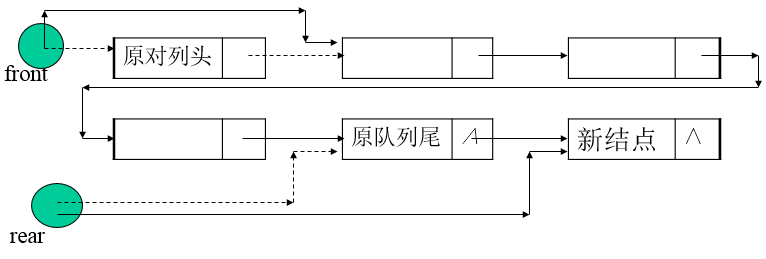
链式队列的操作示意

链式队列的说明

class Queue {
public:
// standard Queue methods
  Queue( );
  bool empty( ) const:
  Error_code append (const Queue_entry &item);
  Error_code serve( );
  Error_code retrieve (Queue_entry &item) const;
// safety features for linked structures
  ~ Queue( ):
  Queue (const Queue &original);
  void operator = (const Queue &Original);
  protected:
    Node *front, *rear;
 }:

链式队列的构造函数与入队列操作

构造函数

Queue:: Queue( )
/* Post: The Queue is initialized to be empty */
{
    front = rear = NULL;
}

入队列操作

Error_code Queue:: append (const Queue_entry &item)
/* Post: Add item to the rear of the Queue and return a code of success or return a code of overflow if dynamic memory is exhausted. */
{
    Node *new_rear = new Node(item);
    if (new_rear = = NULL) return overflow;
    if (rear = = NULL) front = rear = new_rear;
      else {.
          rear － >next = new_rear;
          rear = new_rear;
       }
     return success;
}

链式队列的出队列操作

Error_code Queue:: serve( )
/* Post: The front of the Queue is removed. If the Queue is empty return an Error_code overflow. */
{
    if (front = = NULL) return underflow;
    Node *old_front = front;
    front = old_front － >next;
    if (front = = NULL) rear = NULL;
    delete old_front;
     return success:
}

派生链式队列与其长度函数

class Extended_queue: public Queue {
public:
   bool full( ) const;
   int size( ) const;
   void clear( );
   Error_code serve_and_retrieve(Queue_entry &item);
};
int Extended_queue:: size( ) const
/* post: return the number of entries in the Extended_queue. */
{
    Node *window = front;
    int count = 0;
    while(window ! = NULL) {
        window = window － >next;
        count + +;
    }
    return count;
}

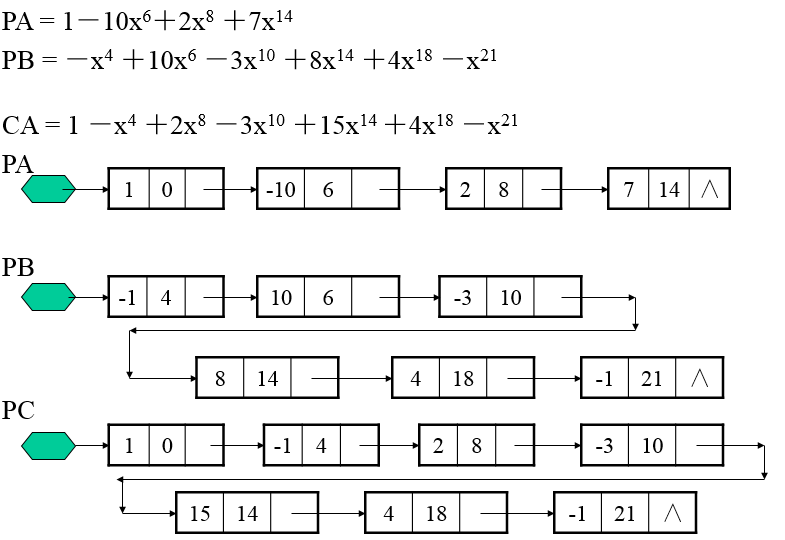
4、多项式及其计算

需要解决的问题：多项式的表示及计算算法。

struct Term {
    int degree;
    double coefficient;
    Term (int exponent = 0, double scalar = 0):
};

Term:: Term(int exponent, double scalar)
/* Post: The Term is initialized with the given coefficient and exponent, or with default parameter values of 0. */
{
    degree = exponent;
    coefficient = scalar;
}

链表的应用

1. 多项式

多项式相加

相加算法思想

多项式存储结构
链式栈、队列、通常的单链表，也可以是连续存储结构。视具体应用需要而定。

多项式的运算
基本程序

int mainO
/* Post: The program has executed simple polynomialarithmetic comi
tered by the user.
Uses: The classes Stack and Polynomial and the functions introductio
tions, do_command, and get_command. */
{
Stack stored_polynomials;
introductionO;
instructionsO;
while (do_command(get_command(), stored_polynomials));
}

多项式运算(do command命令)

bool do_command(char command. Stack &stored_polynomials)
/* Pre: The first parameter specifies a valid calculator command.
Post: The command specified by the first parameter has been applie
Stack of Polynomial objects given by the second parameter. A
true is returned unless command == 'q'.   A"^-" ' S-y*
Uses: The c/asses Stack and Polynomial. */           D     '‘
{
Polynomial p, q, r;
switch (command) {
case '?':
p.readO;
if (stored_polynomials.,push(p) == overflow)
cout « "Warning: Stack full, lost polynomial" « endl;
break;            
case '=':
if (stored_polynomials.empty())
cout « "Stack empty" « endl;
else {
stored_polynomials.top(p);
p.printO;
}
break;
case'+':
if (storecLpolynomials.emptyO)
cout« "Stack empty" « endl;
else{
stored_polynomials.top(p); (?y{i-^a ^<%»/ |,
storecLpolynomials.popO;     3; ^'
if(stored_polynomials.empty()) {
cout « "Stack has just one polynomial" « endl;
stored_polynomials.push(p);
}
else{
»   stored_polynomials.top(q);
stored_polynomials.pop();
r.equals_sum(q, p);     f '^- ^+ P
if (stored_polynomials.push(r) == overflow)
cout « "Warning: Stack full, lost polynomial" « endl;
}
break;
// Add options for further user commands.
case 'q':                 ~^^-
cout « "Calculation finished." « endl;
return false;
}
return true;
}

多项式类的说明

class Polynomial {
public:
void read();
void printO;
void equals_sum(Polynomial p. Polynomial q);
void equals_difference(Polynomial p. Polynomial q);
void equals_product(Polynomial p. Polynomial q);
Error_code equals_quotient(Polynomial p. Polynomial q);
private:
double value;
};
class Polynomial: private Extended_queue { //  Use private inheritance.
public:                                                            .
   void read( );              
   void print( ) const;
   equals_sum(Polyoornial p. Polynomial q);
   void equals_difference(Polynomial p. Polynomial q);           
   void equals_product(Polynomial p. Polynomial q);            
   Error_code equals_quotient(Polynom»al p. Polynomial q);
   int degree() const;    
private:              
   void mult_term(Polynomial p. Term t); 
} 

多项式的打印

void Polynomial:: print( ) const
/* Post: The Polynomial /s printed to cout */
   Node *print_node = front;      
   bool first_term= true;
   while (print.node != NULL) {  
       Term &print_term = print_node->entry;
       if (first_term) {          //  In this case, suppress printing an initial'+'
first_term = false;
        if (print_term.coefficient < 0) cout « " - ";   
}
else if (print_term.coefficient < 0) cout « " - ";
else cout « " + ";
double r = (print_term.coefficient >= 0)   
                   ? print_term.coefficient: -(print_term.coefficient);
if(r != 1) cout « r;
if (print.term.degree > 1) cout « " X"" « print_term.degree;
if (print_term. degree == 1) cout « " X";
if (r == 1 && print_term.degree == 0) cout « " 1";
        print.node = print_node->next;    
        }
       if (first.term)
           cout « “0";           // Print 0 for an empty Polynomial.
       cout« end l;

多项式的读取

void Polynomial:: read( ) 
/* Post: The Polynomial /s read from cin. */ 
{
   clear( );
   double coefficient;     
   int last_exponent, exponent; 
   bool first_term = true;
   cout « "Enter the coefficients and exponents for the polynomial, "
  « "one pair per line. Exponents must be in descending order." « endl
  « "Enter a coefficient of 0 or an exponent of 0 to terminate." «endl;

多项式的读取

do {
       cout « "coefficient? " « flush; 
       cin  »coefficient;              
       if (coefficient != 0.0) {           
          cout « "exponent? " « flush;                    
          cin  » exponent;        
          if ((! first_term && exponent >= last_exponent) || exponent < 0) {
             exponent =0;      
             cout « "Bad exponent: Polynomial terminates without its last term « endl;
           }
         else {
            Term new_term(exponent, coefficient);
            append(new_term);
            first_term = false;
           }
           last_exponent = exponent; 
          }
       } while (coefficient != 0.0 && exponent !=0);
}

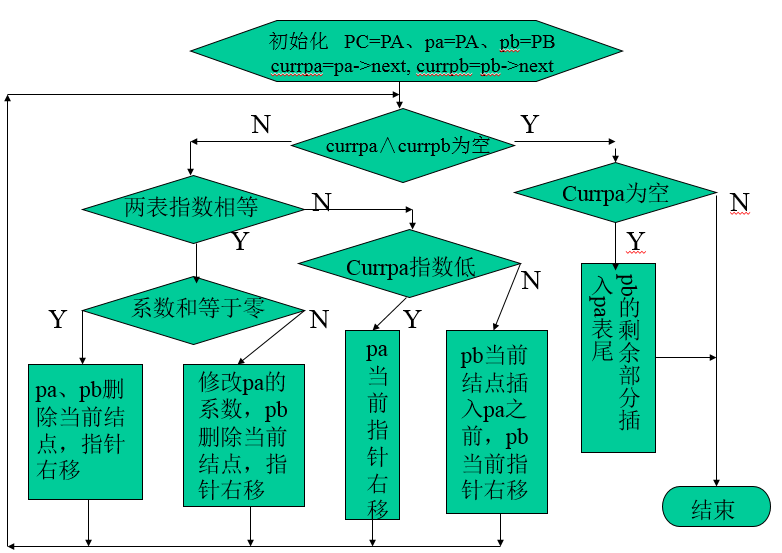
多项式加法

void Polynomial ::equals_sum(Polynomial p, Polynomial q)
/* Post: The Polynomial object is reset as the sum of the two parameters. */
{
    dear( );
    while (!p.empty( ) || !q.empty( )){
        Term p_term, q_term;
        if (p.degree( ) > q.degree( )) {
            p.serve_and_retrieve(p_term);
            append(p_term);
        }
        else if (q.degree( ) > p.degre( )) {
            q.serve_and_retrieve(q_term);
            append(q_term);
         }
        else{
           p.serve_and_retrieve<p_term);
           q.serve_and_retrieve(q_term);
           if (p_term.coefficient + q_term.coefficient ! = 0) {
                Term answer_term(p_term.degree, p_term.coefficient + q_term.coefficient);
                append(answer_term);
            }
        }
    }
}

持续更新中。。。

数据结构Ｃ＋＋语言描述专题系列 （一） 绪论
数据结构Ｃ＋＋语言描述专题系列 （二） 栈
数据结构Ｃ＋＋语言描述专题系列 （三） 队列
数据结构Ｃ＋＋语言描述专题系列 （四） 链式栈和队列
数据结构Ｃ＋＋语言描述专题系列 （五） 递归
数据结构Ｃ＋＋语言描述专题系列 （六） 表与串
数据结构Ｃ＋＋语言描述专题系列 （七） 查找
数据结构Ｃ＋＋语言描述专题系列 （八） 排序
数据结构Ｃ＋＋语言描述专题系列 （九） 表与信息检索
数据结构Ｃ＋＋语言描述专题系列 （十） 二叉树
数据结构Ｃ＋＋语言描述专题系列 （十一） 多路数
数据结构Ｃ＋＋语言描述专题系列 （十二） 集合及其表示
数据结构Ｃ＋＋语言描述专题系列 （十三） 图
数据结构Ｃ＋＋语言描述专题系列 （十四） 波兰表达式