维纳滤波器（Wiener Filter）介绍及公式推导

shannanshouyin

已于 2025-02-23 02:01:57 修改

阅读量5k

点赞数 37

文章标签：算法

于 2024-11-22 09:57:11 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/shannanshouyin/article/details/143954688

版权

一、维纳滤波器介绍

1.1系统输入与输出

维纳滤波器（Wiener Filter）是一种处理离散信号的线性最优滤波器，它的设计目的是使输出信号与期望信号之间的均方误差（MSE）最小化。

输入信号为：

$u(n)=d(n)+v(n)$

$d(n)$ 为期望响应，也就是在不含误差的情况下的理想输出，假设其均值为0（一般会对信号进行减去均值处理），即 $E[d(n)]=0$ ； $v(n)$ 为噪声， $u(n)$ 是滤波器的输入，可以看作是我们实际测量得到的包含误差的原始数据。

输出信号为：

$y(n)=w(n)*u(n)$

$w(n)$ 为维纳滤波器的系数（冲激响应）， $*$ 为卷积符号， $y(n)$ 为滤波器的输出，称为我们的估计量。滤波器系统框图如下：

假设FIR滤波器有M阶，滤波器抽头系数为 $w(0),w(1),w(2),...,w(M-1)$ ,输入为 $u(n),u(n-1),u(n-2),...,u(n-M+1)$ ，滤波器n时刻的输出可以写作：

$y(n)=\sum_{k=0}^{\infty }w_{k}^{*}u(n-k),\; \; \; \; n=0,1,2,...\; \; \; \; (1)$

n时刻滤波器的输出为滤波器冲激响应和滤波器输入的线性卷积，其中，k表示滤波器的第k阶抽头。我们讨论的信号是在复数域的，此时星号 $*$ 表示复共轭。FIR滤波器系统框图为：

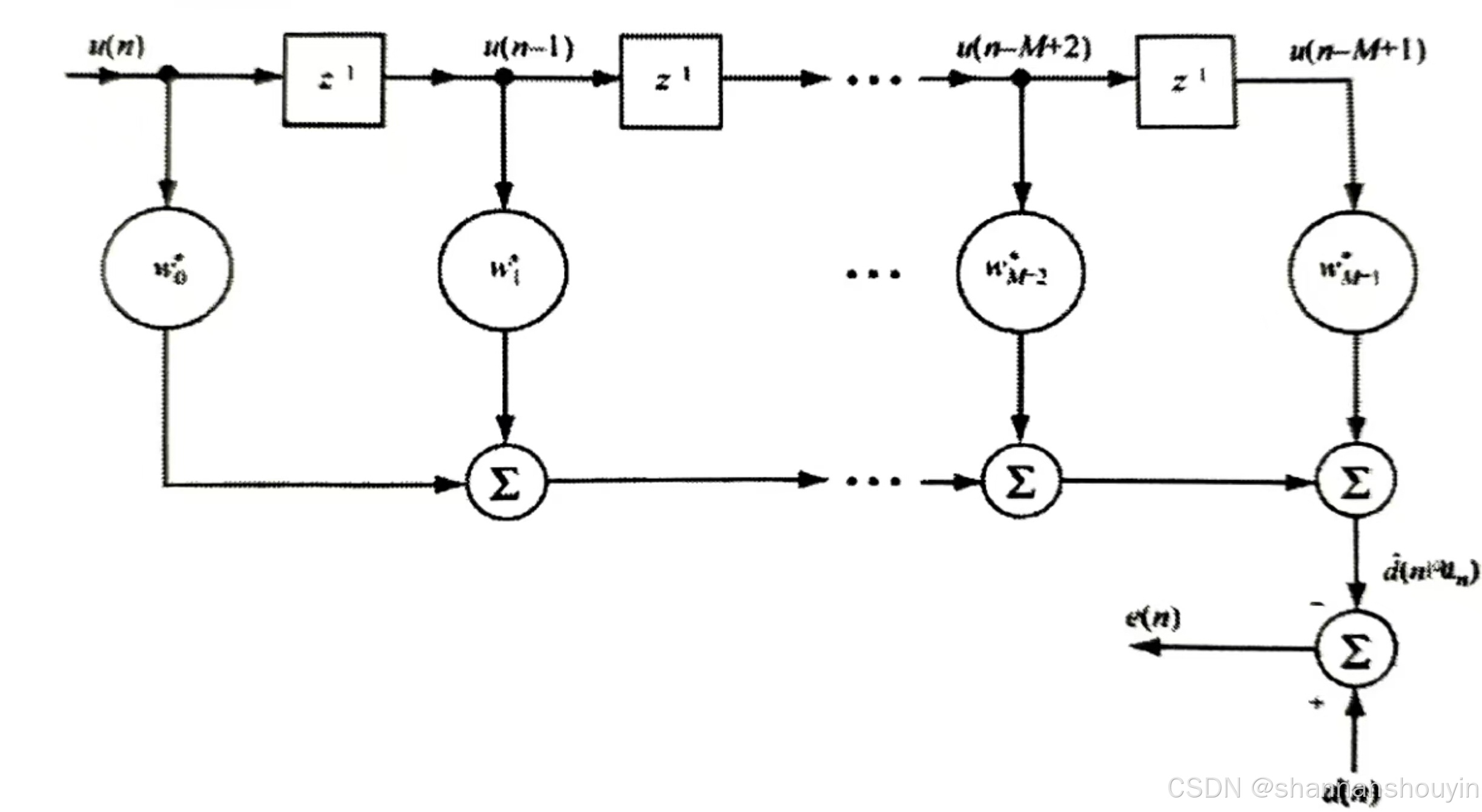
1.2维纳滤波器目标

维纳滤波器的目标是找到线性最优的 $w(n)$ ，使估计量 $y(n)$ 在均方误差意义下最大程度接近我们的期望响应 $d(n)$ ，以上述FIR滤波器为例，估计量与期望相应之差为：

$e(n)=d(n)-y(n)=d(n)-\sum_{k=0}^{M-1}w_{k}^{*}u(n-k)\; \; \; \; (2)$

基于均方误差，我们的目标误差函数为：

$J(w) = E[\left | e(n) \right |^{2}]=E[e(n)e^{*}(n)]\; \; \; \; (3)$

维纳滤波器的目标是使 $J(w)$ 最小，我们需要找到是 $minJ(w)$ 时对应的滤波器系数 $w$ 。

二、维纳-霍夫方程(Wiener-Hopf equation)推导

2.1维纳-霍夫方程推导

为了找到使滤波器输出均方误差最小的系数 $w(n)$ ，首先将(2)带入(3)并展开，得：

最低0.47元/天解锁文章

评论 6

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。