数字图像处理笔记——几何操作（Geometric operations）

几何操作

所谓的几何变换就是对图像进行平移、缩放、翻转等操作。我们将几何操作与之前提到的点操作进行一个对比，我们可以知道点操作是对像素的值进行变换，即点还是原来的点T(x,y)，在这个基础上对灰度值进行T()变换；而几何操作是对坐标进行变换，新的坐标由旧的坐标经过计算得到，二者的灰度值相同

仿射变换与投影变换

对于这一类变换我们可以用矩阵变换表示，我在之前关于VR的博客中也有写到过一点相关内容，但是那个博客还是侧重于三维的旋转

除了上述操作外，还有旋转操作也可以用矩阵表示

上述操作的组合叫做相似变换，如果α,β=±1，那么这种变换叫做等度量变换

除此以外矩阵变换中还包括剪切变换

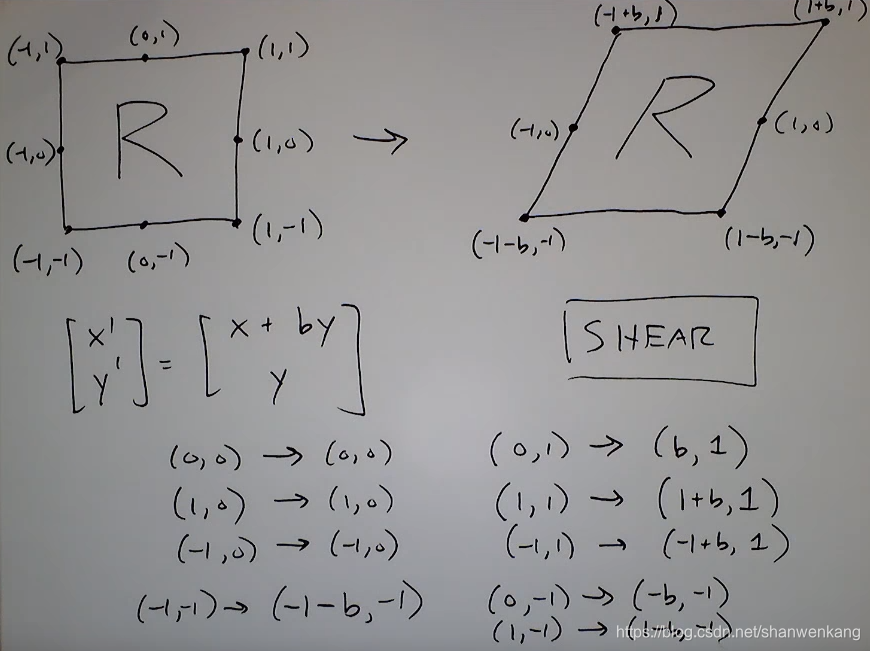
具有以下形式的变换叫做仿射变换，对于仿射变换，matlab中有imwarp函数可供使用来直接进行变换。abcd表示缩放、翻转、剪切等操作，ef表示平移操作

除了仿射变换，还有一种变换叫做投影变换，投影变换是能将矩形变换为四边形的一种变换，即能将平行线变为交线。对于投影变换我们也用一个三维矩阵来表示，其中a11、a12、a21、a22用来表示旋转、放缩等操作，b1、b2用来表示平移操作，c1、c2用来表示投影变换的操作

但是需要注意的是课程中讲的矩阵与matlab中使用的矩阵不大相同，matlab中原图像的像素坐标u,v是作为行向量，左乘以变换矩阵，而课程写的矩阵是把u,v作为列向量右乘以变换矩阵。这就使得matlab中真正控制投影变换的是cf参数，gh参数用来控制平移操作（见下图）。其中cf越大代表原本平行线到交线的汇聚点（vanishing point）离原图越近，cf越小表示越远，c=f=0时表示汇聚点在无穷远处

生成输出图像

如果我们要产生输出的图像，一个很直观的想法就是看看输入图像中的像素映射到输出图像中的哪个位置，但是这存在一个明显的问题就是映射后的位置往往不是不落在输出图像的整数点上，这种情况下计算输出图像中每个像素的值变得十分困难，也很容易出现失真

那么一种解决方法就是采用后向映射，也就是从输出图像中的像素点反推其对应输入图像的像素点，当然这很有可能也不是一个整数，此时就要用到插值的方法

插值方法有三种：nearest、bilinear、bicubic。nearest顾名思义就是取对应理想像素点最近的实际像素点的值作为新的像素值；而bilinear则是根据理想像素点到相邻四个实际像素点的距离来计算输出值；bicubic与bilinear类似，它取了临近16个像素点的值来计算输出值

除了上述提到的这些几何变换，还有一些其他的几何变换例如让画面突出等技术在此就不深入讲了