提高大学生网络问题解决能力的创造性思维方法

提高大学生网络问题解决能力的创造性思维方法

（A creative thinking approach to enhancing the web-based problem

solving performance of university students）

Computers & Education 72 (2014) 220–230

一、概念解析

1.网络问题解决能力

网络问题解决能力是指一个人在网络上检索信息以回答与目标问题相关的一系列问题的能力。随着互联网及通讯科技(ICT)的出现，学校不仅扮演向学生传授知识的角色，而且是培养学生在网络上解决问题的能力，以快速应对多元化社会的关键。有必要通过有关信息检索、识别和重组过程的培训课程，促进学生解决问题的能力，以适应未来不断变化的社会。

2.创造性的解决问题策略

创造性思维是超越所学的原则和创造解决问题的新方法的过程。研究人员指出，这两个过程可以整合成一个单一的复杂过程，即创造性问题解决。图1显示了创造性问题解决模型。它由三个部分组成:

图1，创造性解决问题的三个组成部分和六个阶段

（1）理解问题。这个组成部分包括三个阶段:混乱发现(MF)，指的是确定和选择一个目标、工作或问题;数据发现(DF)，指收集数据，探索第一阶段事实的感受、印象、观察、问题或工作，并确定重点;问题发现(PF)，即发现问题并确认问题;叙述和提炼问题，使之清晰。

（2）产生想法。这个组成部分与第四阶段:创意寻找(IF)有关，这是指尽自己最大的努力找到许多多样化和新颖的想法，选择和替代方法。

（3）行动计划。这个部分包括两个阶段:寻找解决方案(SF)，这是指制定一套评估标准，使用这些标准来评估和澄清在前一阶段发现的所有想法的优点、缺点和适当性，并选择最有用的解决方案;验收发现(AF)，指的是对所选择的解决方案的使用，在实施过程中考虑潜在的阻力和帮助，以及使该解决方案有效地发展和达到特定的行动计划。

3.认知风格

认知风格是指个体通过与环境的互动来思考、感知和处理信息以解决问题的方式。研究者从不同的角度提出了不同的认知风格。不同认知风格的人在感知和处理信息时往往表现出截然不同的行为。

二、研究内容

1.研究背景：

随着信息和通信技术的进步，研究者指出了制定有效的教学策略来提高学生的网络问题解决能力的必要性和挑战，网络问题解决能力是指通过在网络上搜索、抽象和总结信息来调查一系列相关问题的能力。因此，本研究提出了一种将创造性问题解决策略整合到网络学习环境中的创造性思维方法，并在某大学的“信息技术与社会”课程中进行了实验。

2.研究目的：

本研究提出了一种创造性思维策略来应对这一问题。并对某大学两个班级的80名新生进行了实验，以评估所提出方法的有效性。

3.研究对象：

大学护理系两个班新生80人，男23人，女57人，年龄19 ~ 20岁。所有的学生都由同一位老师授课，并且在学习活动之前都有使用电脑和访问网络的经验。一个班被指定为实验组，另一个班被指定为对照组。实验组40名学生采用创造性思维方法进行基于网络的问题解决活动，对照组40名学生采用传统教学方法进行相同的学习活动。

4.研究问题：

为了深入研究该方法的有效性，在分析学生的学习表现时考虑了学生的认知风格。本研究的研究问题如下：

1. 使用创造性思维方法学习的学生是否比使用传统教学的学生有更好的网络问题解决能力?
2. 不同认知风格的学生在创造性思维教学和传统教学中表现出不同的网络问题解决能力吗?

5.研究结果：

实验结果表明，该方法在“问题发现”和“想法发现”两方面均比传统方法提高了学生的网络问题解决能力。

此外，本研究还发现该方法能提高具有直觉型认知风格学生的“事实发现”表现。

三、实验设计

以台湾南部一所大学的“资讯科技与社会”课程为对象，评估该方法的有效性。选修课的目标之一是帮助学生认识到生活环境和社会的问题，并培养他们利用信息技术解决问题的能力。

1.实验对象和方式：为某大学护理系两个班新生80人，男23人，女57人，年龄19 ~ 20岁。

所有的学生都由同一位老师授课，并且在学习活动之前都有使用电脑和访问网络的经验。一个班被指定为实验组，另一个班被指定为对照组。实验组40名学生采用创造性思维方法进行基于网络的问题解决活动，对照组40名学生采用传统教学方法进行相同的学习活动。

2.实验工具：研究采用基于网络的学习系统Meta-Analyzer

Meta-Analyzer允许教师设计一系列递进式问题，引导学生根据学习课程的特定主题构建主题知识，Meta-Analyzer的界面如图2所示。

图2.一个学生在Meta-Analyzer的学生界面中搜索信息回答问题

3.实验流程：实验流程如图3所示

图3.本研究的实验步骤

4.结果：

前后测原始数据

前测t检验：

两组学生的前测成绩经t检验无显著差异(t = 0.382, p>0.05)，说明两组学生在学习活动前的网络问题解决能力基本相当。

后测协方差分析：

表1：两组网络问题解决能力的协方差分析

	组别	N	Mean	SD	df	调整平均值	F	η2
基于网络的问题解决能力	对照组	40	22.48	7.06	77	22.20	4.267	0.09
	实验组	40	26.85	6.90		26.90

为了评估所提出方法的有效性，采用协方差分析(ANCOVA)来检验两组的后测分数，排除前测分数的影响。表1 可知，实验组学生的学习成绩显著优于对照组学生(F(1,78)=4.267,p <0.007)，效应量(η2)大于0.090，显示出较大的效应量。这表明创造性问题解决方法可以提高学生的网络问题解决能力。

（补充：η2(eta squared)是方差分析中常用的效应量。其计算方法η2=SS组间/SS总体

η2=0.0099-0.0588小效应, 0.0588-0.1509中等效应, 大于0.1509大效应）

学生在网络问题解决各维度的测试后得分的原始数据：

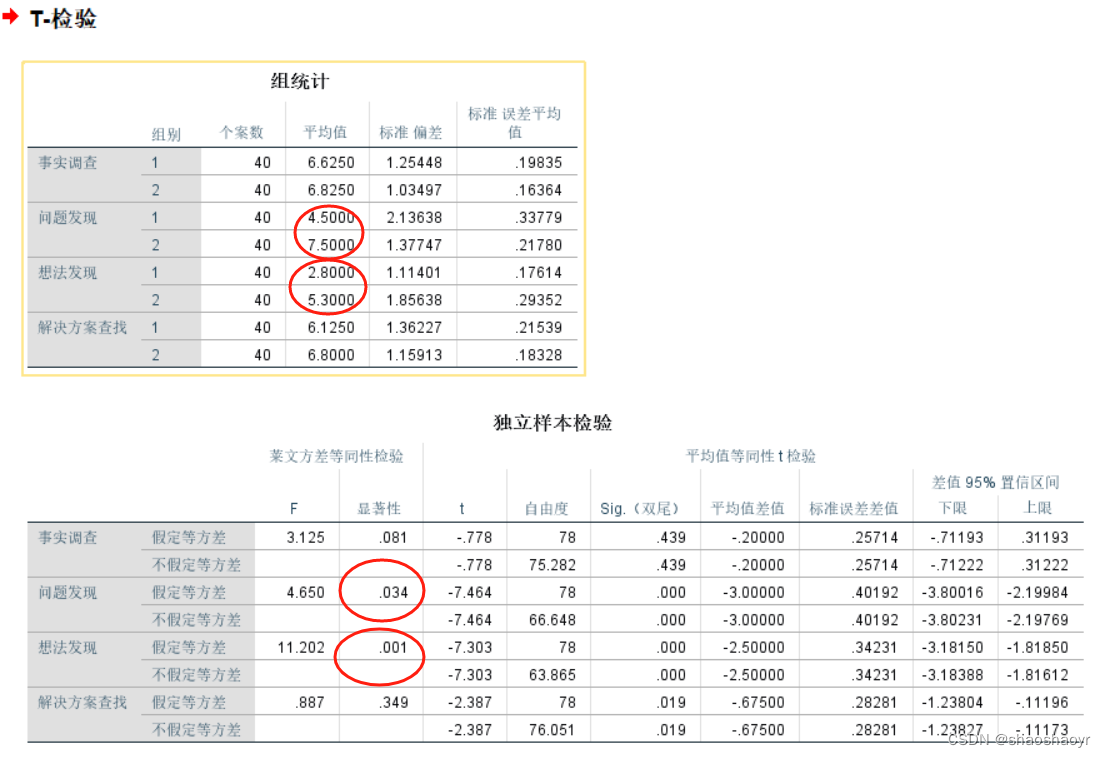
学生在网络问题解决各维度的测试后得分的t检验结果：

问题发现协方差分析：

想法发现协方差分析：

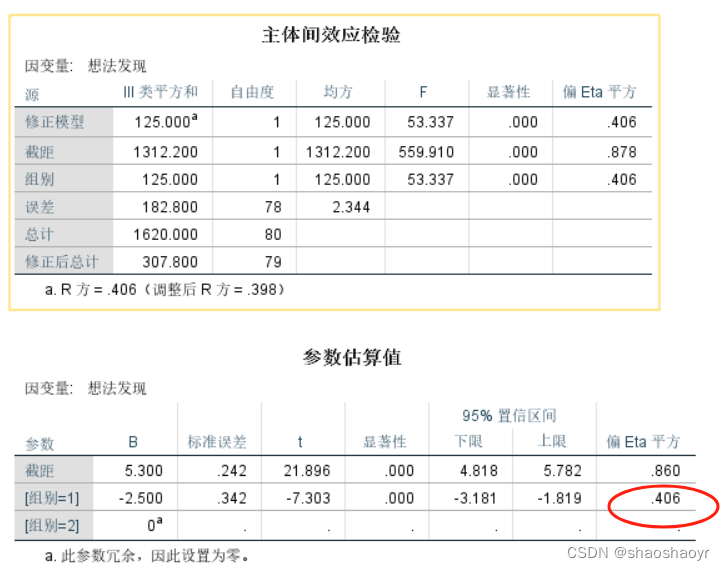
表2 问题解决过程的后测采用独立样本t检验

问题解决过程指标	组别	N	df	Mean	SD	t	偏eta方
事实调查	对照组	40	79	6.63	1.25	-0.778	0.008
	实验组	40		6.83	1.03
问题发现	对照组	40	79	4.50	1.18	-7.464	0.417
	实验组	40		7.50	1.39
想法发现	对照组	40	79	2.80	1.11	-7.303	0.406
	实验组	40		5.30	1.86
解决方案查找	对照组	40	79	6.13	1.36	-2.387	0.068
	实验组	40		6.80	1.16

表2进一步显示了学生在网络问题解决各维度的测试后得分的t检验结果。结果发现，两组学生在问题发现(t=-7.464,p < 0.05)和想法发现(t=-7.303,p < 0.001)两个维度上表现出显著差异，效应量(h2)大于0.14，且表现出较大的效应量。也就是说，创造性解决问题的方法有助于提高学生发现问题和发现想法的能力

表3对两组人的认知风格进行分类

认知方式	组别	分数	学生人数
分析型	对照组	≥55	13
	实验组	≥55	11
直觉型	对照组	≤45	11
	实验组	≤45	11

CSI得分后27%的学生被归类为直觉型，而CSI得分前27%的学生被归类为分析型(Spanier & Tate, 1988)。表5显示了两组中直觉型和分析型学生的数量。

两组认知风格相同的学生的前测成绩的t检验结果。两组相同认知风格学生的前测成绩差异无统计学意义，分析型学生的前测成绩差异为0.22 (p < 0.05)，直觉型学生的前测成绩差异为0.15 (p < 0.05)。也就是说，两组的直觉型和分析型学生在学习活动前都具有相当的基于网络的问题解决能力。

分析型网络问题解决能力的后测协方差分析：

直觉型网络问题解决能力的后测协方差分析：

表3不同认知风格下网络问题解决能力的后测独立样本t检验

认知风格类型	组别	N	df	Mean	SD	t	偏eta方
分析型	对照组	13	23	21.31	1.11	3.42	0.347
	实验组	11		24.55	3.21
直觉型	对照组	11	21	21.27	1.19	4.40	0.492
	实验组	11		28.27	5.14

P<0.05

表3给出了两组认知风格相同学生的后测成绩的t检验结果。结果发现，实验组直觉型学生的测试后得分显著高于对照组(t = 4.40, p < 0.02)，效应量(h2)大于0.14，且具有较大的效应量，这表明创造性问题解决方法对直觉型学生的帮助大于分析型学生。

创造性问题解决策略对分析型学生网络问题解决绩效的原始数据：

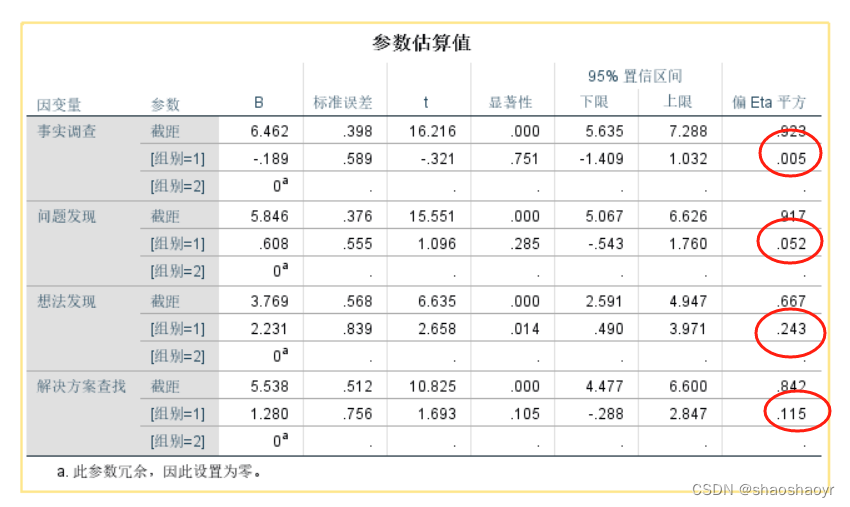
表4分析型学习问题解决过程指标的多元方差分析

问题解决过程指标		对照组（n=13）		实验组（n=11）		F	偏eta方
	df	Means	SD	Means	SD
事实调查	1	6.46	1.51	6.27	1.35	0.103	0.005
问题发现	1	5.85	1.14	6.45	1.57	1.200	0.052
创意发现	1	3.77	2.09	6.00	2.00	7.067	0.243
寻找解决方案	1	5.54	2.33	6.82	0.98	2.867	0.115

P<0.005

表4显示了排除前测影响的多元方差分析结果。结果发现，两组分析型学生在想法发现后验中达到显著水平(F(1,21)=7.067,p < 0.01)，效应量(h2)超过0.14，显示出较大的效应量。也就是说，创造性问题解决方法在提高分析型学生的想法发现表现方面显著受益。

创造性问题解决策略对直觉型学生网络问题解决绩效的原始数据：

直觉型学生问题解决过程指标的多元方差分析：

表5直觉型学习问题解决过程指标的多元方差分析

问题解决过程指标		对照组（n=11）		实验组（n=11）		F	偏eta方
	df	Means	SD	Means	SD
事实调查	1	6.91	1.13	7.82	0.60	5.495	0.216
问题发现	1	5.73	1.01	7.36	1.75	7.232	0.266
创意发现	1	3.45	1.81	6.00	2.00	9.800	0.329
寻找解决方案	1	6.55	4.68	7.27	1.79	0.232	0.011

P<0.05

表5给出了排除前测协方差分析影响的结果。结果发现，实验组直觉型学生在“事实发现”(F(1,20)=5.495,p < 0.05)、“问题发现”(F(1,20)=7.232,p < 0.05)和“想法发现”(F(1,20)=9.800,p < 0.05)方面的表现显著优于对照组，效应量(h2)大于0.14，且表现出较大的差异。

五、结论

在本研究中，提出了一种创造性的问题解决方法来提高学生的网络问题解决能力。

并通过实验对不同认知类型学生的学习表现进行了评价。结果表明，创造性问题解决方法对直觉型学生比分析型学生更有帮助。此外，进一步的分析结果表明，提出的方法可以显著提高分析型学生的想法寻找绩效。同时，提高了直觉型学生的“事实发现”、“问题发现”和“想法发现”的表现。有文献指出，直觉型的人往往会根据自己的感受迅速做出判断，在解决问题时喜欢探索环境，这可能是为什么创造性问题解决方法对直觉型学生的影响大于分析型学生的原因。

因此，本研究为培养学生的思维能力(如搜索能力、创造性思维能力、批判性思维能力和推理能力)以及解决问题的能力提供了潜在的策略。也就是说，开发的基于网络的创造性思维学习环境可以有效地帮助学生以发散和收敛的思维过程想出潜在的解决方案，而不是传统的CPS环境。此外，在一个基于网络的创造性思维环境中，教育者可以有机会调查学生在测试前和测试后解决问题过程中的变化。同时，也显示了该方法在帮助不同认知风格的学生解决个人网络问题方面的有效性。

局限性：

①样本仅限于一组，大学护理专业的学生。

②此外，虽然本研究的重点是认知风格，但应该注意到，其他人为因素也可能影响学习者与互联网的互动，包括情感因素、性别差异和年龄差异。

疑问：1.两组为什么要用方差分析？（偶尔也可以用）

2.在直觉型和分析型学习问题解决过程指标的影响时，排除前侧干扰为什么 一个用多元方差一个不用？

原文章链接：A creative thinking approach to enhancing the web-based problem solving performance of university students - ScienceDirect