【优化】共轭函数(Conjugate Function)超简说明

共轭函数是最优化问题中非常重要的概念，常用来在原问题和对偶问题之间进行转换。
本文从便于理解的角度对其进行介绍，并推导常见例子。
本文主要参考S. Boyd and L. Vandenberghe, Convex Optimization中3.3节。

定义

对于原函数$f(x),x\in D$，其共轭函数为：
$$f^{\ast }(y)=\underset{x\in D}{\sup }(<y,x>-f(x))$$

其中，$<y,x>$表示两个变量的内积

• 对于标量：$<y,x>=y\cdot x$
• 对于向量：$<y,x>=y^{T}x$
• 对于$n\times n$对称矩阵：$<y,x>=\text{tr}(yx)$

特别注意，共轭函数的定义域要求对$x\in D$，$<y,x>-f(x)$有上界。即，$f^{\ast }(y)$不能为无穷大。

物理意义

对于共轭函数的每一个自变量$y=\bar{y}$，其取值相当于一条直线与原函数之差的最大值：
$$f^{\ast }(\bar{y})=\underset{x\in D}{\sup }(l(x)-f(x))$$
这条直线$l(x)=<\bar{y},x>$，其斜率由$\bar{y}$决定。

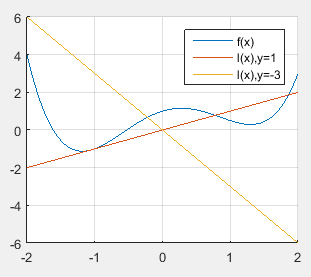
两条曲线之差随着$x$变化，其最大值可以对$x$求导得到：
$$\frac{\partial (<y,x>-f(x))}{\partial x}=0\Rightarrow f^{\prime }(x)=y$$
即：曲线斜率与直线斜率相同处的$x$，能够得到最大值。
$$f^{\ast }(\bar{y})=<\bar{y},\bar{x}>-f(\bar{x}),subjecttof(\bar{x})=\bar{y}$$

举例

Negative entropy

原函数：$f(x)=x\log x,x>0$

原函数为增函数。
对于$y<0$，$l(x)$为减函数。则$l(x)-f(x)$为减函数，不超过其在零点取值。
对于$y\ge 0$，$l(x)$也是增函数
$$\underset{x\to \infty }{\lim }l(x)/f(x)=\underset{x\to \infty }{\lim }{l}^{\prime }(x)/f^{\prime }(x)=\underset{x\to \infty }{\lim }y/(\log x+x)=0$$

$l(x)$增速小于$f(x)$增速，故其差有界。

故，$f^{\ast }(y)$的定义域为$y\in R$。

找到最大值处$x$的表达式：
$$\frac{xy-x\log x}{\partial x}=0\Rightarrow x=e^{y-1}$$
代入共轭函数：
$$f^{\ast }(y)=y\cdot e^{y-1}-e^{y-1}(y-1)=e^{y-1}$$