本文主要是本人看论文和网上视频博客的总结和个人的理解思路,如有错误感谢指正
一、扩散模型
1.介绍
扩散模型属于基于概率分布的生成式模型,终极目的是拟合数据的分布。区别于以往的自编码器模型、GAN模型等,扩散模型不直接对
建模。
是实际的数据分布,通常非常复杂,过去方法用网络来表示这一分布,即用
拟合
。扩散模型试图通过对N步去噪过程建模来避免直接拟合
。(注意:我们用
表示拟合的或者人为设置的分布,用
表示实际的分布)
2.建模过程
扩散模型假设N步去噪过程是一个马尔可夫过程,即每一步去噪仅依赖于上一步去噪的输出来得到
。因此模型产生输出的过程是从分布
采样一个样本
,再从给定
情况下的条件分布
中采样出
,再从给定
情况下的条件分布
中采样出
,...,一直重复上面过程直到采样出
即为模型的输出。
用更加形式化的方式表示上面过程。分布可以表示为
,其中
表示
的联合分布,
可以看作是一系列隐变量。从联合分布中把隐变量积分掉就得到余下那个变量的分布。当然我们不会真的去求一个分布的积分,主要是是我们不知道这个分布。所以实际做法就是上面提到的采样。
根据条件概率公式以及上面提到的马尔可夫假设
,联合分布
可以表示为
。我们现在的目标是如何求出分布
以及分布
。
记是人为选定的对分布
的近似,
是用模型拟合的对分布
的近似。于是对联合分布
的近似表示为
。
很容易理解的一点是,如何去噪取决于加的噪声,也就是我们加上了什么噪声那么我们就要减去一个同样的噪声(看起来像废话,但后面我们会看到,DDPM实际上就是做的就是预测加的噪声)。在DDPM中,加噪声的操作是人为设计的,而且加的噪声的分布是人为选定的。DDPM加噪声的这一步操作采用高斯分布,也就是服从高斯分布
。为什么要选择高斯噪声呢?个人认为主要原因是高斯噪声足够简单,高斯噪声只包含均值和方差两个参数,涉及到高斯分布的运算包括加减乘除和KL散度等都比较简单。因为加噪过程是高斯分布,原论文假设在每一步变化比较小的情况下
也符合高斯分布,所以代码实现中
序列的变化必需足够缓慢,这导致加噪过程通常都有成百上千步,同样逆过程也需要成百上千步,后续有论文如DDIM优化采样的过程来减少步数。对于
,我们可以看到
时,分布
与
无关,所以我们认为此时
,所以上面的
我们可以简单地取标准高斯分布。其中
是事先确定的逐渐增大的参数序列(论文中称作variance shedule 或者beta shedule)。此时联合分布
可以表示为
,
。其中除了
未知外,其他都是已知的。我们知道
,带入上面的近似分布
得到对数据集分布
的近似拟合
,注意到此时表达式中已经不包含未知项(要么是模型拟合得到的项,要么是预先定义的项),接下来要考虑的就是如何优化这个拟合的分布(优化其中模型相关的部分)。
3. 优化
(1)要最小化的目标L
考虑最小化负的对数似然函数,论文中的目标还加上了一项KL项(KL散度大于等于0,论文说法是变分界限),因此有
上面的式子可以进一步写成(利用马尔可夫性和条件概率公式)
其中
进而
注意到第二项中的连加可以相消(),于是上面等于下面
进而可将L化简为如下(这里q具体是怎么变化的原论文没讲,一般机器学习中不会真的求期望,而是通过采样的方法解决,每个小的batch size产生的L表达式中期望内的值认为是L的无偏估计,因此可以通过采样加梯度下降实现优化,也就是这里的期望实际可以忽略。注:从数据集取图片出来就是一个采样过程,KL代表KL散度)
上面第一项记为,第二项求和内的部分记为
,第三项记作
,其中
是常数,实际训练时不会使用
(2) 怎么求
怎么求
重参数化技巧:从分布采样等价于先从分布
采样出
,计算出
作为分布
的采样结果。
高斯分布性质:
首先证明一个性质,任意时刻的可以由
序列来近似的产生。
记 另外
由和重参数化技巧,从
采样等价于
从而
前面我们提到论文假设是高斯分布,我们认为这里
也是高斯分布,即
由条件概率公式,有
t =
(马尔可夫性)
高维高斯分布,因为已经假设结果为高斯分布,所以我们忽略exp前面的系数来求均值和方差,注意前面方差
因此
由*(1)公式知,代入上面得
(3) 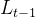 化简
化简
在上面提到
因为前面提到论文假设每步改变很小得情况下认为符合高斯分布。
所以可以有如下表示 *(3)
论文中固定或者上面的
,当然也可以改变模型通道数或者用另一个模型来预测该方差。
官方代码中的预测v目标即指需要预测该方差,只不过不是直接预测方差。官方代码提供了固定方差还是预测方差的选项。
多元高斯分布KL散度公式如下:
因此
最优情况是
论文再次利用重参数化并假定上面等式左右两边有相同形式,从而将任务从预测方差转到预测噪声,即
* (4)
从而
去除两个常系数即得到论文中提到的最终的目标损失。这里看到,模型最终转为预测中加入的随机量的噪声(高斯噪声)
4.采样
(1)论文采样方式
论文算法的采样方式由*(3)和*(4)公式得到分布不断采样得到。初始从标准高斯分布采样得到
不断用重参数化从分布采样,即如下公式
最终得到即输出
(2)直接采样
论文提到可以利用公式直接进行采样,其中
但是这样采样得到的效果不好







 本文介绍了扩散模型的基本概念,包括其作为生成式模型的工作原理,去噪过程中的马尔可夫假设,以及DDPM(变分自编码器)中的高斯噪声应用。重点讲解了优化过程中的目标函数和采样策略,指出直接采样效果不佳的问题,并预告了分数扩散模型部分的内容。
本文介绍了扩散模型的基本概念,包括其作为生成式模型的工作原理,去噪过程中的马尔可夫假设,以及DDPM(变分自编码器)中的高斯噪声应用。重点讲解了优化过程中的目标函数和采样策略,指出直接采样效果不佳的问题,并预告了分数扩散模型部分的内容。














 796
796

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








