深度学习入门基础讲义

工作确定以后，闲暇时间做了如下一个PPT讲义，用于向实验室新生介绍深度学习。他们大部分在本科期间学习通信相关专业课程，基本没有接触过图像处理和机器学习。

对于一个研究生而言，自学应当是一个最基本也是最重要的能力。自学不仅是独立学习，更是主动学习。因此，该讲义的目的主要是使其对深度学习有一个初步的认识，并顺便了解一些常见的概念。 而真正走进深度学习，还需要各自的努力。

该讲义尽量用一些浅显的话语来介绍。囿于水平，一些讲解可能存在模糊甚至错误的情况，欢迎大家提出宝贵的意见。此外，希望补充某些内容，也可以留言或者私信。

PPT中有些图来自于网络，如果有侵权可以联系删除。

讲义下载：deeplearning讲义第一版 http://pan.baidu.com/s/1i4Jo3tz 密码：nxf9

讲义整体包含三部分：

• 相关基础
• 深度卷积神经网络
• 深度学习应用示例

一、相关基础

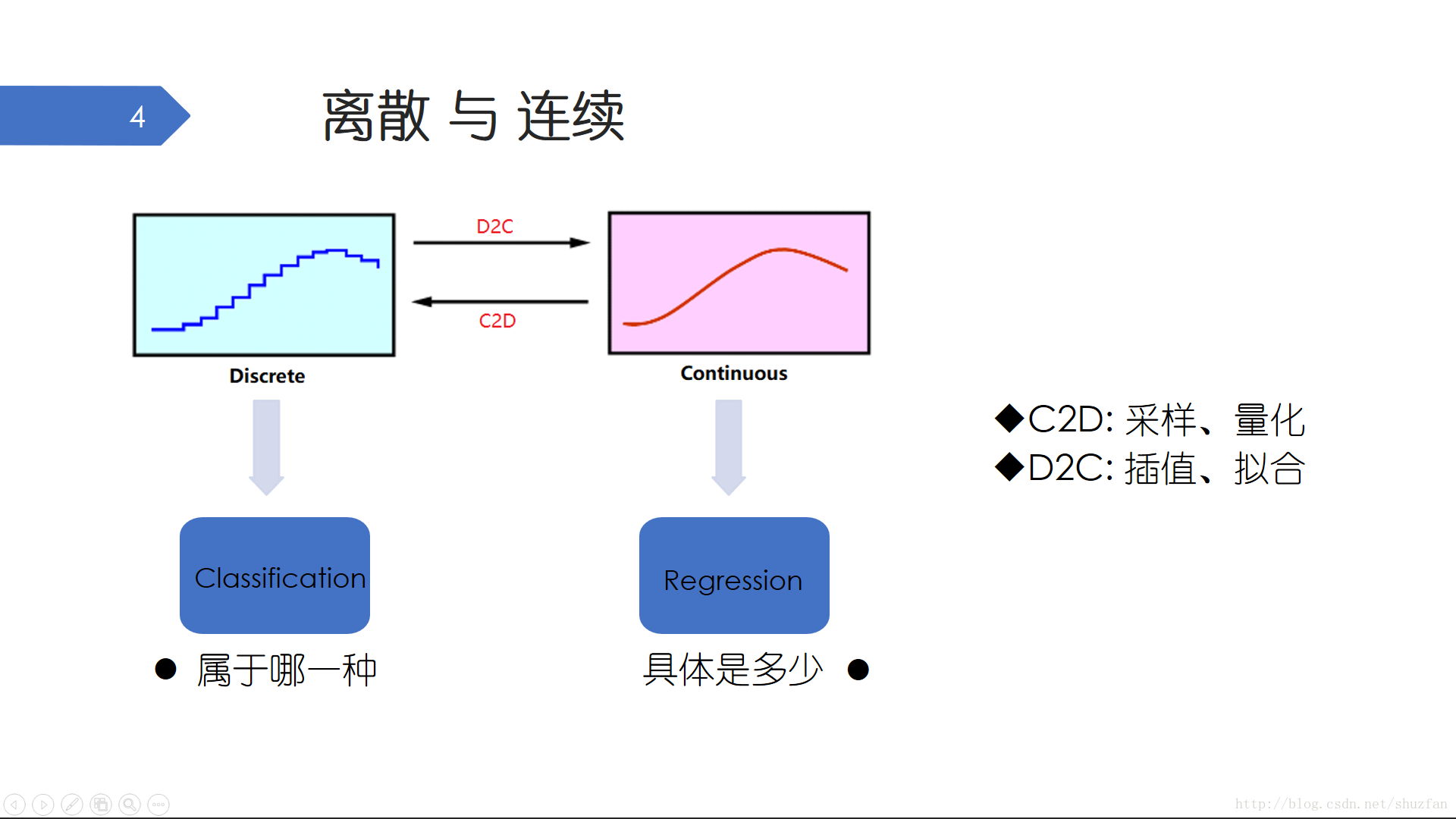
关于世界是离散还是连续的目前还没有定论，但多数人倾向于 “世界是连续的，认知是离散的”。 对于通信系统或者信号处理专业的同学而言，离散和连续是一对熟悉而又重要的概念，它们可以相互转化。我们通常采用 采样量化 的方式将连续信号转化为离散信号，比如声卡设备的采集原理(稍好点的声卡都可以调节采样频率以及位深度等参数)。离散信号转化为连续信号通常采用 插值拟合 的方式来进行逼近，比如等高线地图的绘制、游戏地图的渲染。

对于机器学习而言，几乎所有的任务都可以归类为 离散的分类 任务和 连续的回归 任务。当我们面对一个机器学习问题时，可能需要以离散和连续的角度从宏观上认识该问题，并注意离散和连续的转化。

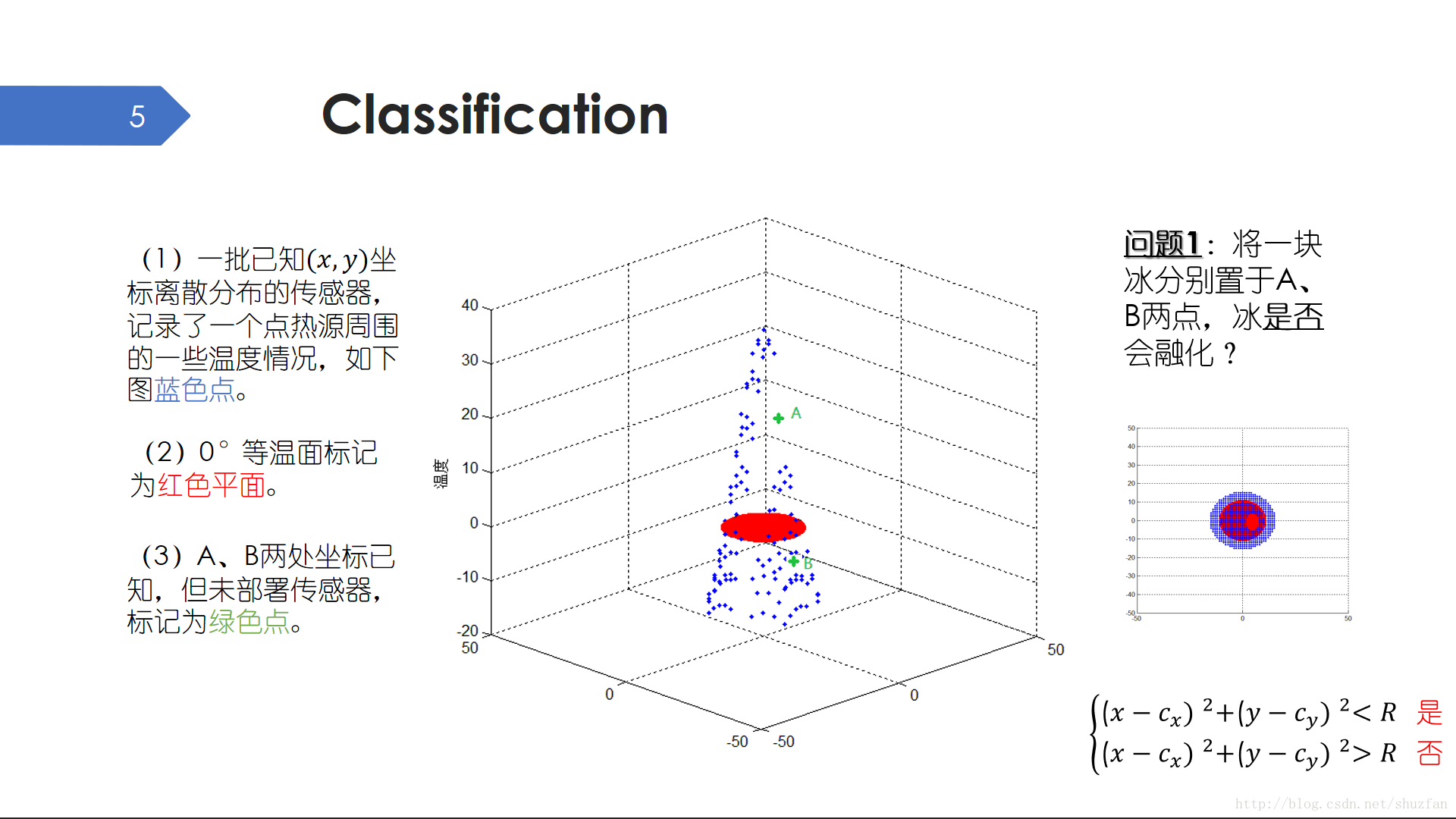
分类是一个典型的离散问题。如上面的三维空间点图，每一个蓝色点都是点热源附近的一个温度传感器。可惜的是，由于传感器部署位置以及损坏的原因，在绿色点A和B我们没有测得有效的温度数据。现在的问题是，如果我们将一块冰分别置于A和B两点，冰是否
会融化？

“是或者不是”，这是一个典型的二分类问题。解决这个问题很简单，我们甚至根本不用具体知道A和B两点的温度。我们只需要设定一个距离阈值，然后计算A、B两点距点热源的距离是否大于该阈值就可以了。

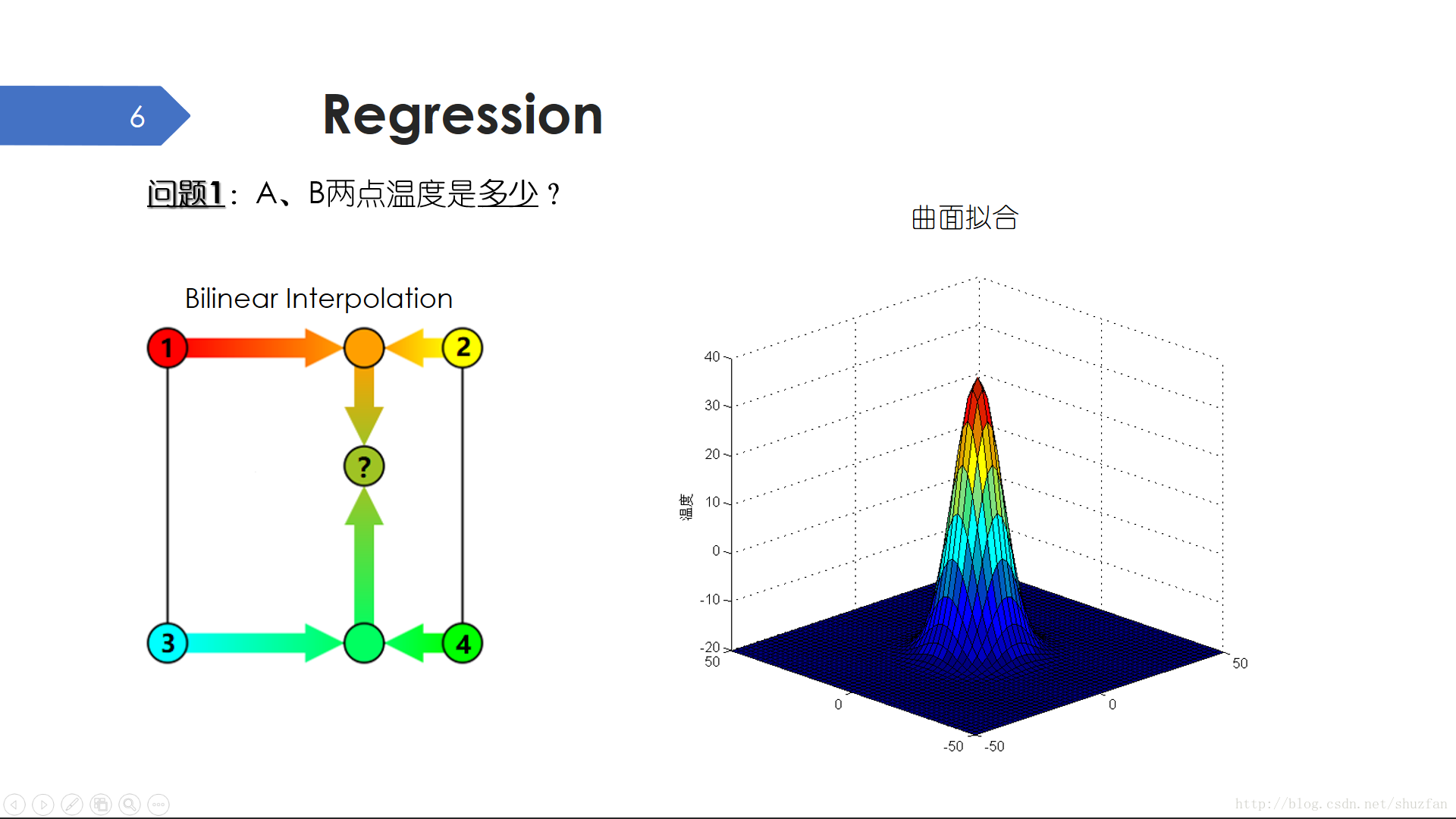
回归是一个典型的离散到连续的问题。还是上面的图，如果我们想要知道A、B两点的具体温度该怎么办？

一个常见的方法是 “插值”,比如左图所示的 “双线性插值”。最简单的双线性插值是用未知点周围4个已知点的数值加权得到，加权系数由未知点到已知点的距离决定。具体操作时常采用先水平加权再垂直加权的方式。

插值仅仅利用了未知点附近的信息，没有考虑全局的分布。事实上，传感器所测量的温度恰好符合如右图所示的高斯曲面。于是，如果我们找到了这样一个可以尽可能描述温度数据分布的曲面方程，那么A、B两点的温度直接就可以知道了。

通过上面的例子，我们除了要认识到“离散”和“连续”之间的区别，也要学会思考二者之间的联系。毕竟，如果知道了具体的温度，也就直接解决了那块冰会不会融化的问题。

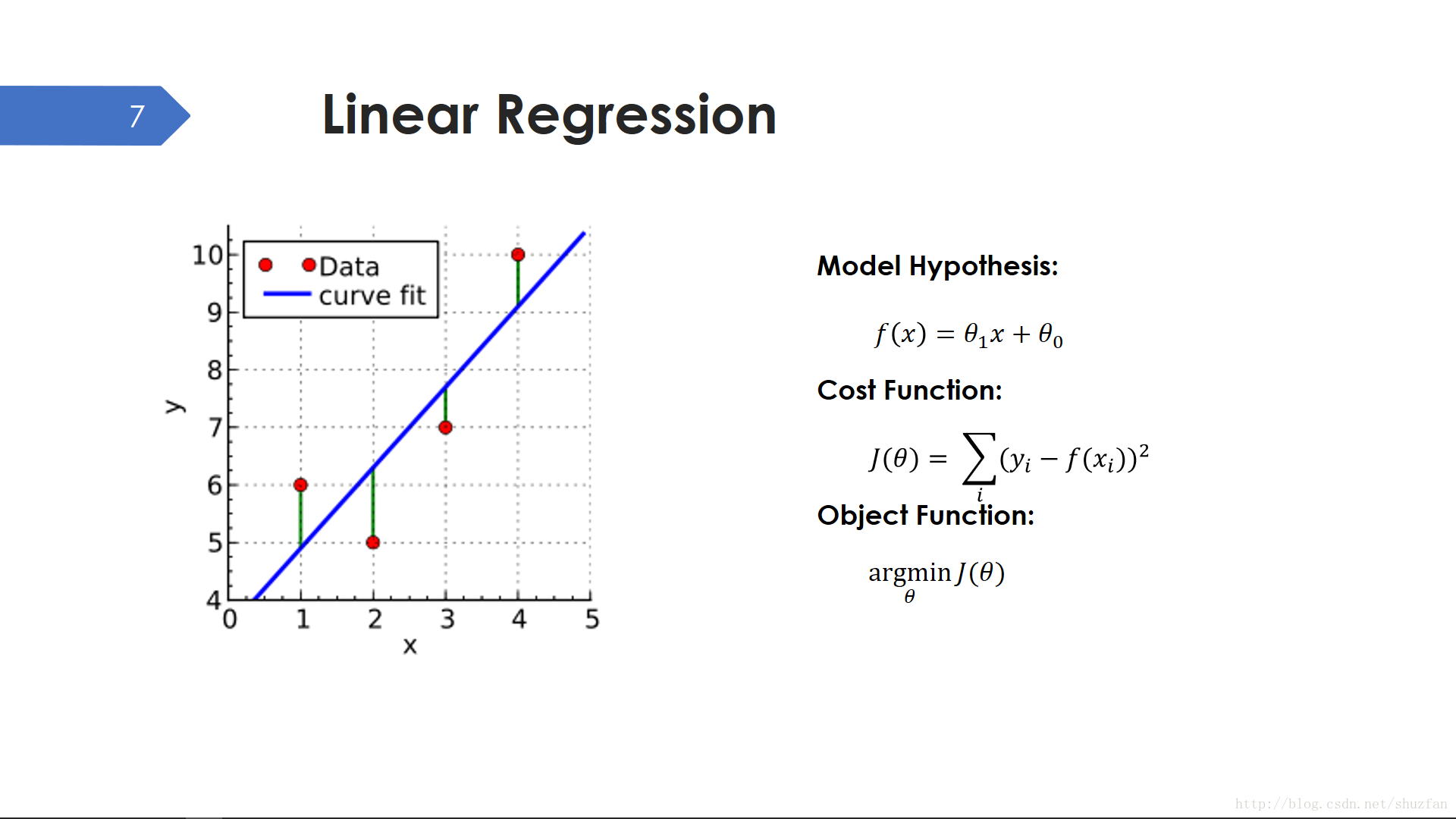
线性回归可以说是最简单的也是我们接触最早的机器学习方法，因为线性回归出现在很多中学数学教材中。线性回归的问题很简单，如上右图所示，寻找一条最“贴合”的直线。所以我们假设的模型就是一条直线，有2个未知参数(斜率和截距)；然后我们继续定义一个代价函数(有些地方也称损失函数 loss function)，这个代价函数其实就是一个欧氏距离平方和；最后我们的目标函数就是最小化代价。

模型假设 —— 代价函数 —— 目标函数，基本是解决一个机器学习问题所必备的三个要素和步骤。

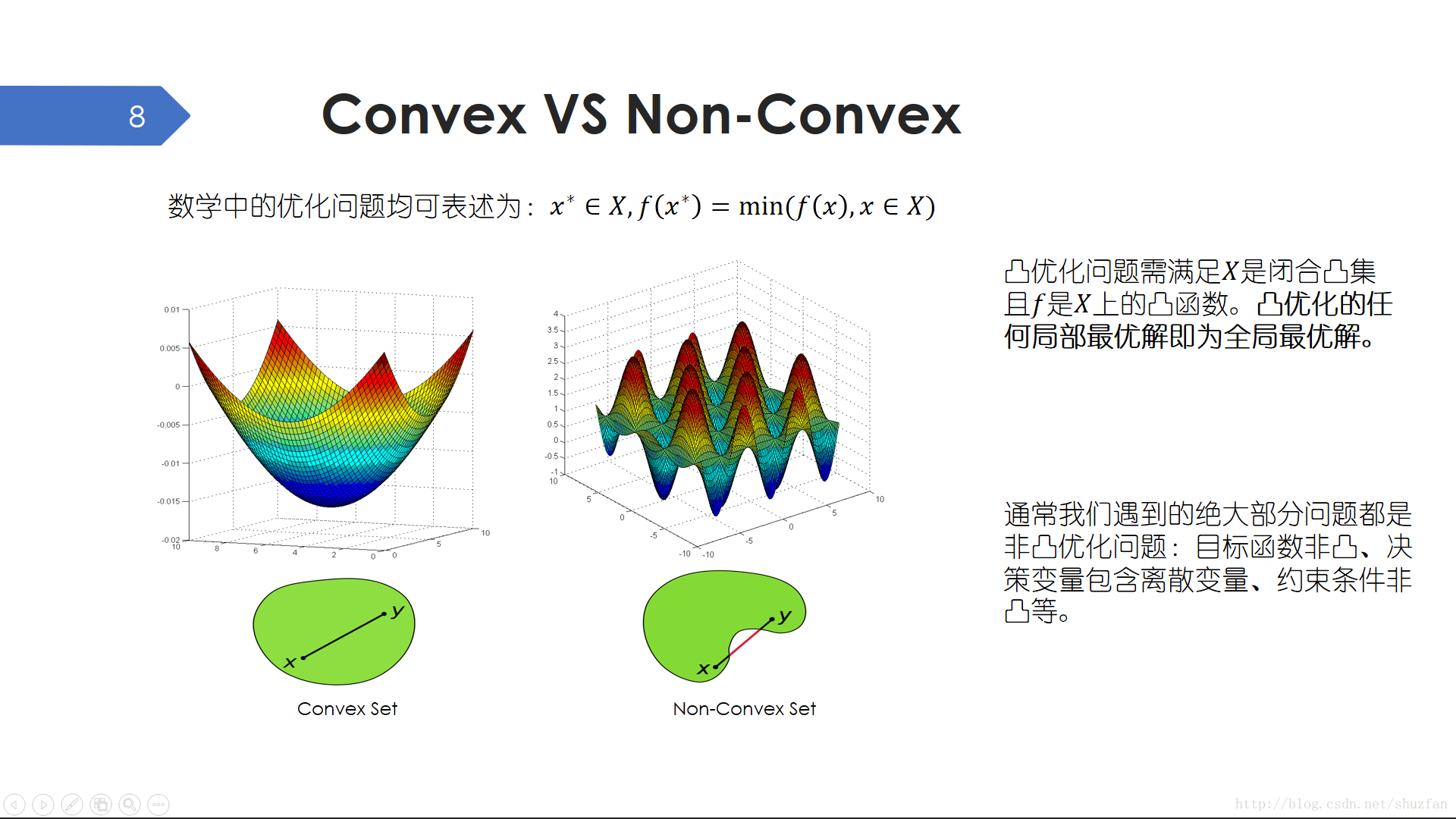
数学中所有的优化问题都可以描述为在一个解空间中找到使目标值最小的解的问题。然后，这类最优化问题又可以被分为 凸优化 和 非凸优化问题。 凸优化是一个非常简单的问题，并且有着一个特别好的性质：任何局部最优解即为全局最优解。但是，绝大部分实际问题都是非凸的，直观上体现为解空间有着很多局部最小点。

幸好，我们的直线拟合问题是一个简单的凸优化问题，其有着唯一最优解(当数据点对称分布时可能不满足)。

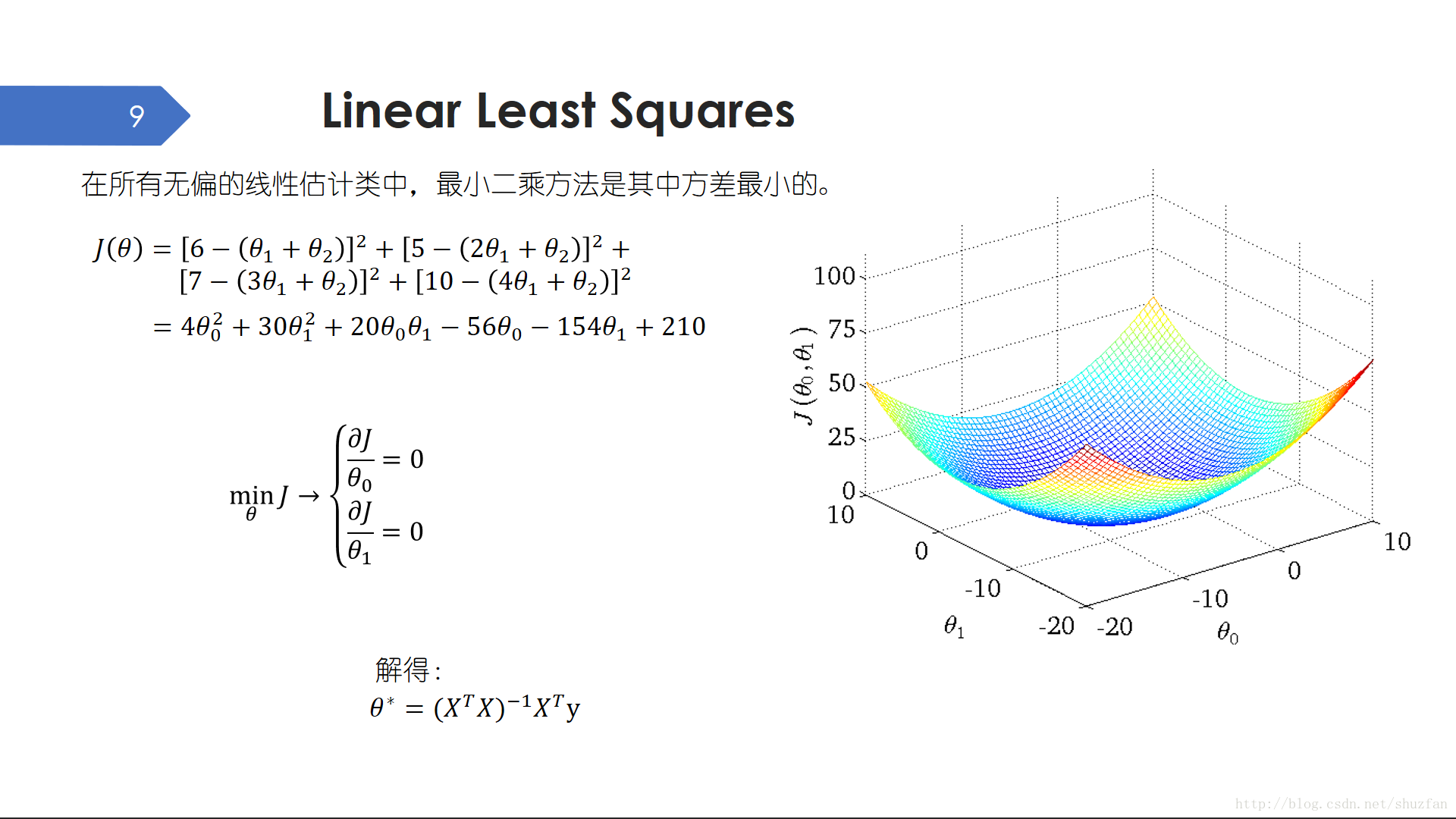
为了求解直线参数，我们之前定义了最小化误差的平方和作为我们的损失函数。为什么用误差平方和而不是用误差绝对值？误差的立方？

于是，我们又要引入最小二乘法（又称最小平方法）这种数学优化技术。在所有无偏的线性估计类中，最小二乘方法是其中方差最小的。

当我们把数据点带入目标函数并整理，我们发现这只是一个简单的双变量二次函数，其解空间如上右图所示，即只有一个全局最小点。 此时，极值点即为全局最小点。因此，我们令偏导数为0，则可以求出一个解。

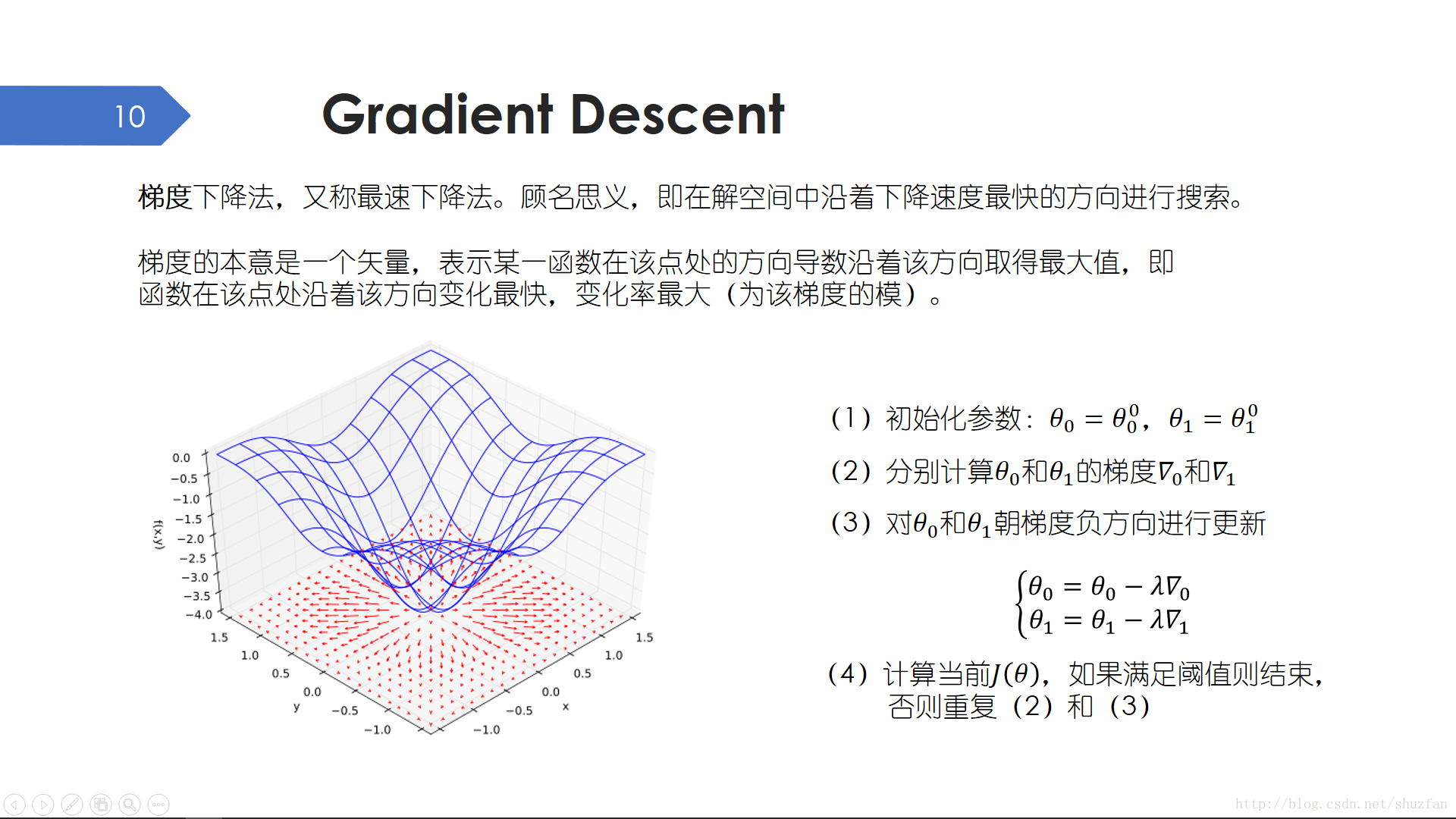
上面我们已经根据偏导为0求出了线性回归的统一解，但是这种方法并不是一直有效的，特别是矩阵求逆困难或者不能求逆时。为此，这里引入另外一种经典的数值优化方法 —— 梯度下降法。

梯度下降法，又称最速下降法。顾名思义，即在解空间中沿着下降速度最快的方向进行搜索。最简单的，一条直线，其梯度就是其斜率，那么我们沿着斜率的反方向移动，数值下降的最快。上左图中蓝色曲线表示 \(f(x,y)=-(cos^2x+cos^2y)^2\), 下面的红色箭头表示每一点的梯度。

于是，简单的梯度下降方法就是初始化参数后不断迭代执行 计算梯度 <——> 更新参数，直至目标函数值满足要求。

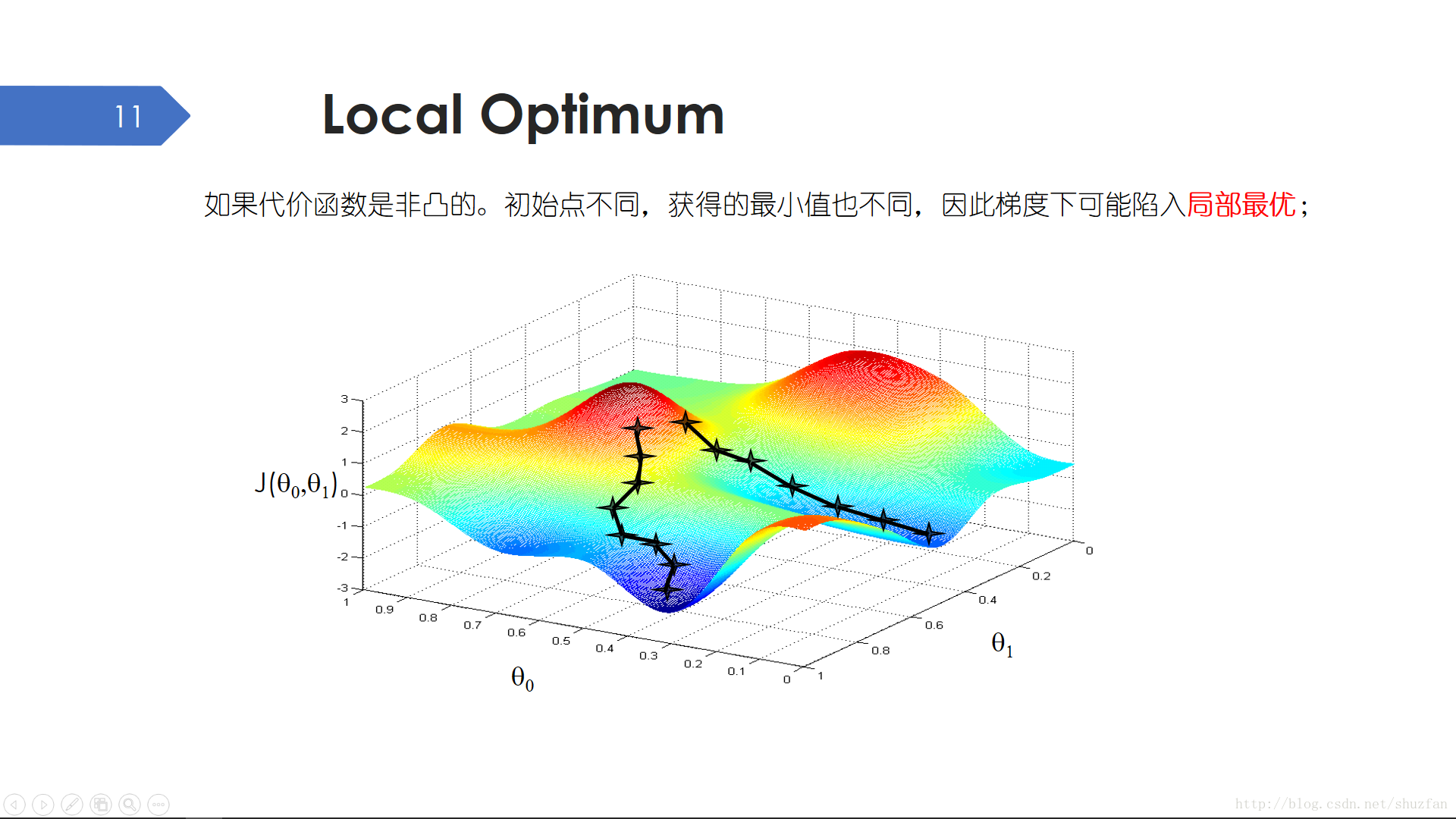
由于梯度下降算法需要随机初始化参数，因此当解空间有多个极小值点时，梯度下降算法有可能会陷入局部最优。

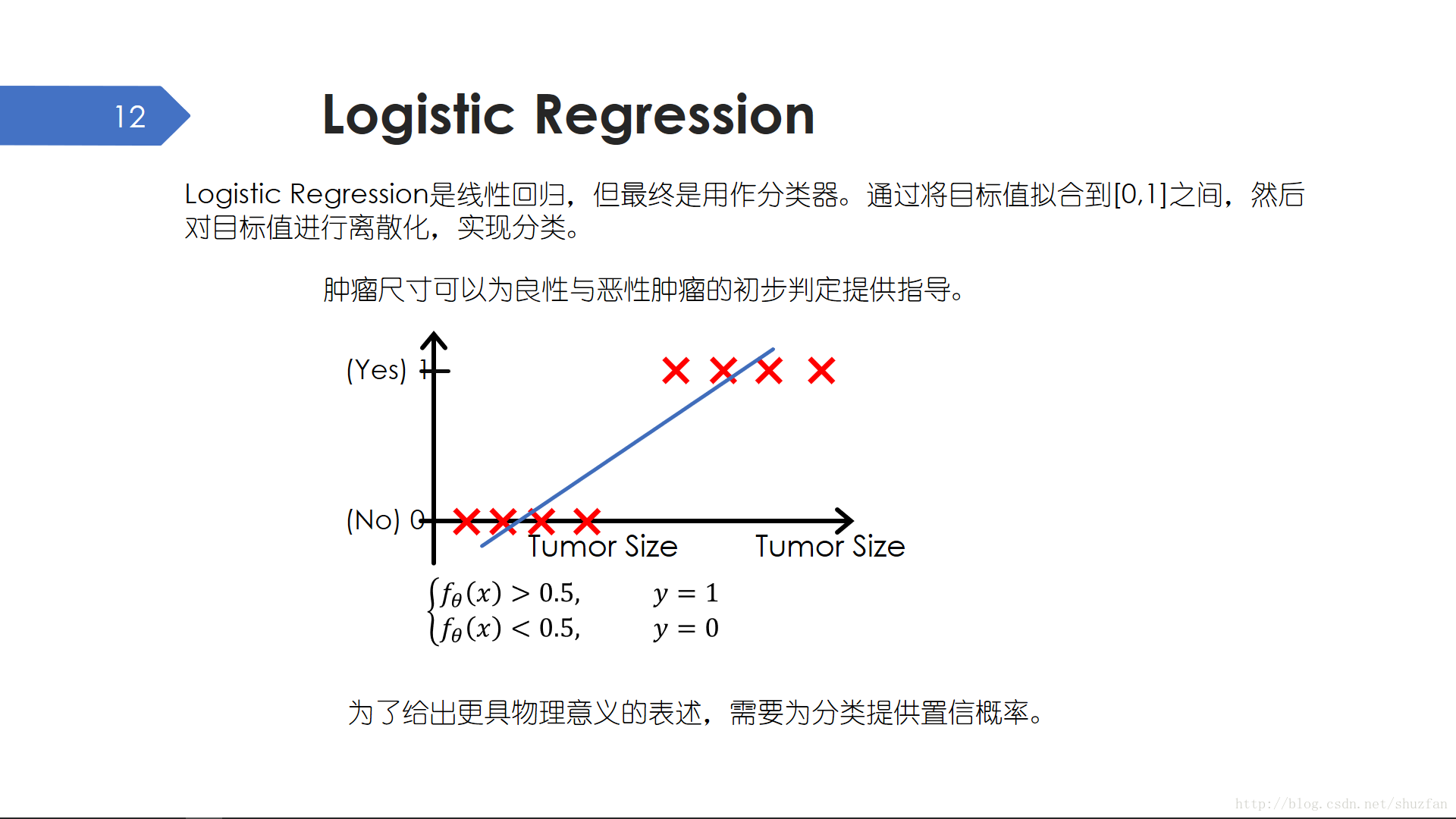
线性回归用于连续数值回归，逻辑回归则用做离散的二分类。比如，肿瘤可以分为良性肿瘤与恶性肿瘤，一般需要病理切片才可以确诊，但可以通过观察肿瘤尺寸来为初步判定提供指导。上图横轴表示肿瘤尺寸，纵轴非0即1表示是否为恶性肿瘤。我们可以利用前面的线性回归方法找到一条直线，然后医生诊断时可以将患者的肿瘤尺寸代入直线方程，如果回归得到的数值大于0.5则判断为恶性肿瘤。

上面的例子其实说明了：回归 + 判决 ——> 分类。

但是，如果患者问医生：“我有多大几率是恶性肿瘤？” 医生该怎么回答。