动态规划—钢条切割问题与01背包问题

最新推荐文章于 2022-05-30 17:17:50 发布

SethCurry

最新推荐文章于 2022-05-30 17:17:50 发布

阅读量1.2k

点赞数

分类专栏： C# 文章标签：动态规划算法

本文链接：https://blog.csdn.net/shymayumi/article/details/120862207

版权

C# 专栏收录该内容

16 篇文章

订阅专栏

本文深入探讨了如何使用动态规划解决钢条切割和01背包问题，旨在最大化收益和背包价值。介绍了自顶向下和自底向上的递归方法，以及备忘录技巧，以避免重复计算，提高算法效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1，穷举法（把所有情况列出来，比较得到总价值最大的情况）

1、钢条切割问题

假定我们知道sering公司出售一段长度为I英寸的钢条的价格为pi(i=1,2,3….)钢条长度为整英寸如图给出价格表的描述（任意长度的钢条价格都有）

先给我们一段长度为n的钢条，问怎么切割，获得的收益最大 rn?

考虑n=4的时候

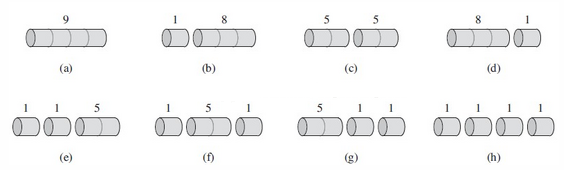
假如一个最优解把n段七个成了k段（1<=k<=n）,那么最优切割方案：

最大收益：

第一种求最优解方案：

对于 r n (n>=1)，最优切割收益：

将切割方案分成下面几种

1，不切割收益为pn

2，将它切割成两半，切割成两半的情况有，对每种情况求最优解

(1,n-1) (2,n-2) (3,n-3) (4,n-4) ..... (n-1,1)

对这两半分别求最优解,最优解的和就是当前情况的最优解

第二种求最优解方案：

我们从钢条的左边切下长度为i的一段，只对右边剩下长度为n-i的一段继续进行切割，对左边的不再切割。这样，不做任何切割的方案就是：当第一段长度为n的时候，收益为pn，剩余长度为0，对应的收益为0。如果第一段长度为i，收益为pi：

代码实现 - 自顶向下递归实现

/****************************************************
 *  功能：钢条切割问题—递归实现
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    private int n = 5;//我们要切割售卖的钢条的长度
    private int[] p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//索引代表钢条的长度  值代表价格

    void Start()
    {
        Debug.Log(UpDown(7, p));
    }
    /// <summary>
    /// 自顶向下的递归方法
    /// </summary>
    /// <param name="n"></param>
    /// <param name="p"></param>
    /// UpDown(1,p):n=1  i=1  maxPrice=p[1]+UpDown(0,p)=1  maxPrice=1
    /// UpDown(2,p):n=2  i=1  maxPrice=p[1]+UpDown(1,p)=1+1=2   i=2  maxPrice=p[2]+UpDown(0,p)=5  maxPrice=5
    /// UpDown(3,p):n=3  i=1  maxPrice=p[1]+UpDown(2,p)=1+5=6   i=2  maxPrice=p[2]+UpDown(1,p)=5+1=6  i=3  maxPrice=p[3]+UpDown(0,p)=8  maxPrice=8
    /// UpDown(4,p):n=4  i=1  maxPrice=p[1]+UpDown(3,p)=1+8=9   i=2  maxPrice=p[2]+UpDown(2,p)=5+5=10  i=3  maxPrice=p[3]+UpDown(1,p)=8+1=9  i=4  maxPrice=p[4]+UpDown(0,p)=9  maxPrice=10
    /// <returns></returns>
    public static int UpDown(int n,int[]p)//求长度为n的最大收益
    {
        if (n == 0) return 0;//终止条件
            int tempMaxPrice = 0;//临时最大收益
        for (int i = 1; i < n + 1; i++)//i的最大值为n
        {
            int maxPrice = p[i] + UpDown(n - i, p);//p[i]+(n-i)的最大收益
            if (maxPrice > tempMaxPrice)
            {
                tempMaxPrice = maxPrice;//跟新
            }
        }
        return tempMaxPrice;
    }
}

分析效率，关于上述方法的运行性能时间问题。

动态规划的方法进行求解

上面的方法之所以效率很低，是因为它反复求解相同的子问题。因此，动态规划算法安排求解的顺序，对每个子问题只求解一次，并将结果保存下来。如果随后再次需要此子问题的解，只需查找保存的结果，不必重新计算。因此动态规划的方法是付出额外的内存空间来节省计算时间。

动态规划有两种等价的实现方法（我们使用上面的钢条切割问题为例，实现这两种方法）

第一种方法是带备忘的自顶向下法

此方法依然是按照自然的递归形式编写过程，但过程中会保存每个子问题的解（通常保存在一个数组中）。当需要计算一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了计算时间；如果没有保存过此解，按照正常方式计算这个子问题。我们称这个递归过程是带备忘的。

/****************************************************
 *  功能：钢条切割问题—带备忘的自顶向下法
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    ArrayList al = new ArrayList(); //用于保存长度为n的最大收益
    private int[] p = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };//索引代表钢条的长度  值代表价格
    void Start()
    {
        Debug.Log(al.Count);
        Debug.Log(UpDown(7, p, al));
        Debug.Log(al.Count);
        Debug.Log(UpDown(8, p, al));
        Debug.Log(al.Count);
    }
    /// <summary>
    /// 带备忘的自顶向下的递归方法
    /// </summary>
    /// <param name="n"></param>
    /// <param name="p"></param>
    /// UpDown(1,p):n=1  i=1  maxPrice=p[1]+UpDown(0,p)=1  maxPrice=1
    /// UpDown(2,p):n=2  i=1  maxPrice=p[1]+UpDown(1,p)=1+1=2   i=2  maxPrice=p[2]+UpDown(0,p)=5  maxPrice=5
    /// UpDown(3,p):n=3  i=1  maxPrice=p[1]+UpDown(2,p)=1+5=6   i=2  maxPrice=p[2]+UpDown(1,p)=5+1=6  i=3  maxPrice=p[3]+UpDown(0,p)=8  maxPrice=8
    /// UpDown(4,p):n=4  i=1  maxPrice=p[1]+UpDown(3,p)=1+8=9   i=2  maxPrice=p[2]+UpDown(2,p)=5+5=10  i=3  maxPrice=p[3]+UpDown(1,p)=8+1=9  i=4  maxPrice=p[4]+UpDown(0,p)=9  maxPrice=10
    /// <returns></returns>
    public static int UpDown(int n, int[] p, ArrayList al)//求长度为n的最大收益
    {
        if (n == 0) return 0;//终止条件
        int tempMaxPrice = 0;//临时最大收益
        if (al.IndexOf(n).Equals(0))//结果已经被计算保存
        {
            return al.IndexOf(n);//返回结果不做保存
        }
        for (int i = 1; i < n + 1; i++)//i的最大值为n
        {
            int maxPrice = p[i] + UpDown(n - i, p, al);//p[i]+(n-i)的最大收益
            if (maxPrice > tempMaxPrice)
            {
                tempMaxPrice = maxPrice;//跟新
            }
        }
        int temp = tempMaxPrice;
        al.Clear();
        al.Add(temp);
        return temp;
    }
}

第二种方法是自底向上法

首先恰当的定义子问题的规模，使得任何问题的求解都只依赖于更小的子问题的解。因而我们将子问题按照规模排序，按从小到大的顺序求解。当求解某个问题的时候，它所依赖的更小的子问题都已经求解完毕，结果已经保存。

/****************************************************
 *  功能：钢条切割问题—自底向上法   n既为长度  也为list所在列表的索引值
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    List<int> list = new List<int>(); //用于保存长度为n的最大收益
    private int[] p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//索引代表钢条的长度  值代表价格

    void Start()
    {
        Debug.Log(BottomUp(10,p,list));
    }
    /// <summary>
    /// 自底向上法
    /// </summary>
    /// <param name="n"></param>
    /// <param name="p"></param>
    /// <returns></returns>
    public static int BottomUp(int n,int[]p, List<int> list)//求长度为n的最大收益
    {
        list.Add(0);
        for (int i = 1; i < n + 1; i++)//i的最大值为n
        {
            //下面取得钢条长度为i的时候的最大收益
            int tempMaxPrice = 0;//临时最大收益
            for (int j = 1; j <=i ; j++)//求i的最优解   遍历从1-i
            {
                //int maxPrice = p[j] + al.IndexOf(i-j);//p[i]+(n-i)的最大收益
                int maxPrice = p[j] + (int)list[i - j];
                if (maxPrice > tempMaxPrice)
                {
                    tempMaxPrice = maxPrice;//跟新
                }
            } list.Add(tempMaxPrice);
        }
        int temp = list[n];
        list.Clear();
        return temp;
    }
}

2、01背包问题

问题描述：

假设现有容量m kg的背包，另外有i个物品，重量分别为w[1] w[2] ... w[i] （kg）,价值分别为p[1] p[2] ... p[i] （元）,将哪些物品放入背包可以使得背包的总价值最大？最大价值是多少？

（示例一：m=10 i=3 重量和价值分别为 3kg-4元 4kg-5元 5kg-6元）

1，穷举法（把所有情况列出来，比较得到总价值最大的情况）

如果容量增大，物品增多，这个方法的运行时间将成指数增长

/****************************************************
 *  功能：01背包问题—穷举法
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    private int m;//背包的容量
    private int[] w = {0, 3, 4, 5};//物品的重量   w[0]代表第0个物品
    private int[] p = {0, 4, 5, 6};//物品的价格   w[0]代表第0个物品
    void Start()
    {
        Debug.Log(Exhaustivity(10,w,p));//取得容量为10的背包的最大总价值
    }
    /// <summary>
    /// 穷举法获取最大总价值
    /// </summary>
    /// <param name="m"></param>
    /// <param name="w"></param>
    /// <param name="p"></param>
    /// <returns></returns>
    public static int Exhaustivity(int m,int[]w,int[]p)
    {
        int i = w.Length-1;//取得物品的个数
        int maxPrice = 0;//最大总价值
        for (int j = 0; j < Mathf.Pow(2,m) ;j++)//遍历i从0开始，到2的m次方   物品数量为i  有2的i次方中取法
        {
            //把j转换成i位的二进制  取得j上某一位的二进制值
            int weightTotal = 0;//重量的和
            int priceTotal = 0;//价格的和
            for (int k = 1; k <= i; k++)//递归取得这个数字上某一位的值
            {
                int result=Get2(j, k);//取得j上第k位的数字
                if (result==1)
                {
                    weightTotal += w[k];
                    priceTotal += p[k];
                }
            }
            if (weightTotal<=m&&priceTotal>maxPrice)//找到价值更大的方案
            {
                maxPrice = priceTotal;//记录最大价格
            }
        }
        return maxPrice;//返回最大价值
    }
    /// <summary>
    /// 取得j上number位的二进制值 是1还是0
    /// </summary>
    /// <param name="j"></param>
    /// <param name="number"></param>
    /// <returns></returns>
    public static int Get2(int j,int number)
    {
        int A = j;
        int B = (int)Mathf.Pow(2, number - 1);//第number位相当于2的number-1次方
        int result = A & B;
        return result==0?0:1;//结果=0返回0  否则返回1
    }
}

2，动态规划算法

我们要求得i个物体放入容量为m(kg)的背包的最大价值（记为 c[i，m]）。在选择物品的时候，对于每种物品i只有两种选择，即装入背包或不装入背包。某种物品不能装入多次（可以认为每种物品只有一个），因此该问题被称为0-1背包问题

对于c[i，m]有下面几种情况：

a、c[i,0]=c[0,m]=0

b、c[i,m]=c[i-1,m] w[i]>m（最后一个物品的重量大于容量，直接舍弃不用）

w[i]<=m的时候有两种情况，一种是放入i，一种是不放入i

不放入i c[i,m]=c[i-1,m]

放入i c[i,m]=c[i-1,m-w[i]]+p[i]

c[i,m]=max(不放入i，放入i)

递归实现（不带备忘的自顶向下法）

/****************************************************
 *  功能：01背包问题—递归实现（不带备忘的自顶向下法）
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    private int m;//背包的容量
    private int[] w = {0, 3, 4, 5};//物品的重量   w[0]代表第0个物品
    private int[] p = {0, 4, 5, 6};//物品的价格   w[0]代表第0个物品
    void Start()
    {
        Debug.Log(UpDown(10,3,w,p));//取得容量为10的背包的3个物品的最大总价值
    }
    /// <summary>
    /// 动态规划算法获取最大总价值
    /// </summary>
    public static int UpDown(int m, int i,int[] w, int[] p) //背包容量 个数  重量  价值  返回值为m可以存储的最大价值
    {
        if (i == 0 || m == 0) return 0;//容量或个数为0
        if (w[i]>m)//最后一个物品的重量大于容量，直接舍弃不用
        {
            return UpDown(m,i-1, w, p);//最多放到底i-1个
        }
        else
        {
            int maxValue1 = UpDown(m - w[i], i - 1, w, p)+p[i];
            int maxValue2 = UpDown(m, i - 1, w, p);
            return maxValue1 > maxValue2 ? maxValue1 : maxValue2;
        }
    }
}

递归实现（带备忘的自顶向下法）

/****************************************************
 *  功能：01背包问题—递归实现（带备忘的自顶向下法）
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    private int m;//背包的容量
    public static int[,] result = new int[11, 4];//创建保存结果的二维数组  测试的最大值为11,3
    private int[] w = {0, 3, 4, 5};//物品的重量   w[0]代表第0个物品
    private int[] p = {0, 4, 5, 6};//物品的价格   w[0]代表第0个物品
    void Start()
    {
        Debug.Log(UpDown(10,3,w,p));//取得容量为10的背包的3个物品的最大总价值
    }
    /// <summary>
    /// 动态规划算法获取最大总价值
    /// </summary>
    public static int UpDown(int m, int i,int[] w, int[] p) //背包容量 个数  重量  价值  返回值为m可以存储的最大价值
    {
        if (i == 0 || m == 0) return 0;//容量或个数为0
        if (result[m,i]!=0)//结果被记录
        {
            return result[m, i]; //直接返回结果
        }
        if (w[i]>m)//最后一个物品的重量大于容量，直接舍弃不用
        {
            result[m,i]=UpDown(m,i-1, w, p);//最多放到底i-1个
            return result[m, i];
        }
        else
        {
            int maxValue1 = UpDown(m - w[i], i - 1, w, p)+p[i];
            int maxValue2 = UpDown(m, i - 1, w, p);
            result[m,i]= maxValue1 > maxValue2 ? maxValue1 : maxValue2;
            return result[m, i];
        }
    }
}

动态规划—自底向上法

/****************************************************
 *  功能：01背包问题—动态规划(自底向上法)
*****************************************************/
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Test : MonoBehaviour
{
    private int m;//背包的容量
    public static int[,] result = new int[11, 4];//创建保存结果的二维数组
    private int[] w = {0, 3, 4, 5};//物品的重量   w[0]代表第0个物品
    private int[] p = {0, 4, 5, 6};//物品的价格   w[0]代表第0个物品
    void Start()
    {
        Debug.Log(BottomUp(10,3,w,p));//取得容量为10的背包的3个物品的最大总价值
    }
    /// <summary>
    /// 动态规划(自底向上法)获取最大总价值
    /// </summary>
    public static int BottomUp(int m, int i,int[] w, int[] p) //背包容量 个数  重量  价值  返回值为m可以存储的最大价值
    {
        if (result[m,i]!=0) return result[m, i];
        for (int tempM = 1; tempM < m+1; tempM++)//从1遍历到m  嵌套循环遍历  从小问题遍历到我们要解决的问题
        {
            for (int tempI = 1; tempI < i+1; tempI++)//内层循环
            {
                if (result[tempM, tempI] !=0)continue;
                if (w[tempI] > tempM)//j中放不下w[k]
                {
                    result[tempM, tempI] =result[tempM, tempI - 1];
                }
                else
                {
                    int maxValue1 = result[tempM - w[tempI], tempI - 1] + p[tempI];
                    int maxValue2 = result[tempM, tempI - 1];
                    result[tempM, tempI] = maxValue1 > maxValue2 ? maxValue1 : maxValue2;
                }
            }
        }
        return result[m, i];
    }
}