笔记︱横截面回归模型中调节效应+中介效应（横截面回归模型两大方向）

笔者认为一般统计模型中的横截面回归模型中大致可以分为两个方向：一个是交互效应方向（调节、中介效应）、一个是随机性方向（固定效应、随机效应）。

两个方向的选择需要根据业务需求:

交互效应较多探究的是变量之间的网络关系，可能会有很多变量，多变量之间的关系；

而随机性探究的是变量自身的关联，当需要着重顾及某变量存在太大的随机因素时（这样的变量就想是在寻在内生变量一样，比如点击量、不同人所在地区等）才会使用。具体见：R语言︱线性混合模型理论与案例探究（固定效应&随机效应）

调节效应

Y与 X的关系受到第三个变量M的影响
调节变量可以是定性的 (如性别) ，也可以是定量的 (如年龄)
影响因变量和自变量之间关系的方向 (正或负 )和强弱

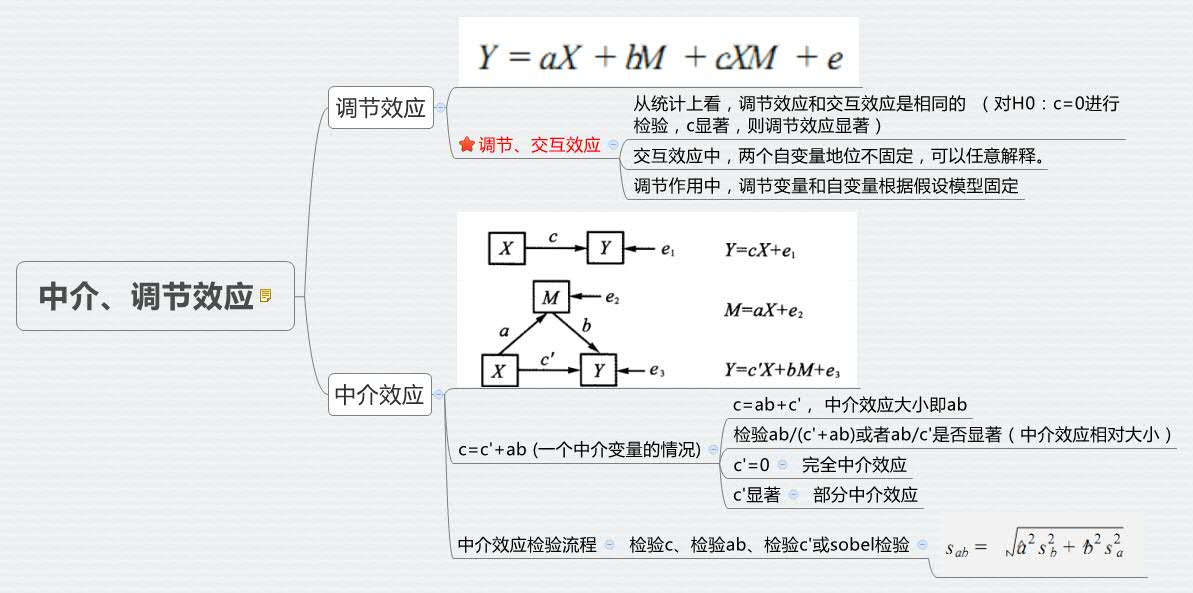
调节效应和交互效应

从统计上看，调节效应和交互效应是相同的
                      （对H0：c=0进行检验，c显著，则调节效应显著）
从概念上看，交互效应中，两个自变量地位不固定，可以任意解释。
                        调节作用中，调节变量和自变量根据假设模型固定。

中介效应

如果X通过影响变量 M来影响Y,则称M为中介变量
c是X对Y的总效应，a、b是经过中介变量M的中介效应
c=c'+ab (一个中介变量的情况)

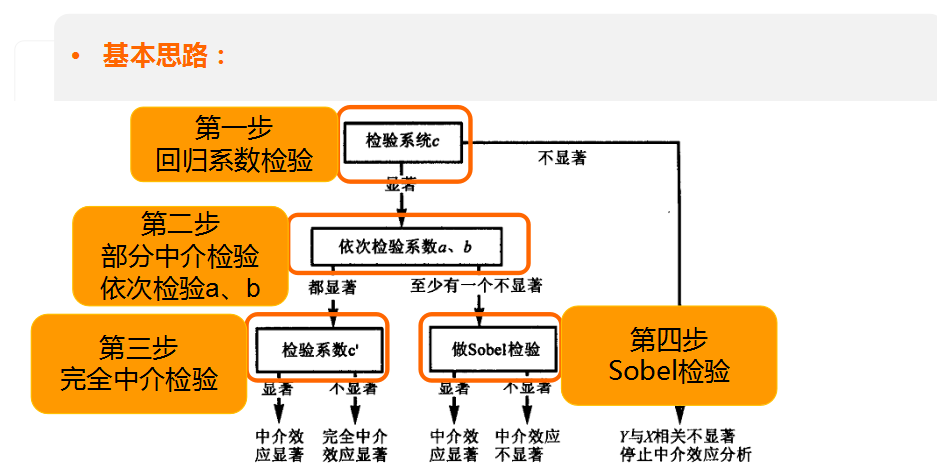
侯杰泰等提出的中介效应检验程序

两个效应的对比：

1、调节效应比较容易实现，通过交互项既可以获取；但是中介效应需求验证的东西较多，也较为复杂。

————————————————————————————————————————————————

效应的建模

1、调节效应的建模

在建模过程中，是否需要加入其它变量来进行调和。作者在后来的思考中觉得，为了使模型尽量简洁，应该选择第一种方案。

第一种方案：y~x1+x2+x1*x2

第二种方案：y~x1+x2+x1*x2+x3+x4+x5

检验的是x1*x2的系数是否显著，若显著则代表存在交互效应=x1 、x2独立。业务思考的出发点在：两变量相互独立。

一般的解释：两个自变量对因变量的影响并不是独立的，任何一个自变量的作用都会受到另一个自变量的影响。

若存在多个交互效应，比如：

y~x1+x2+x1*x2+x3+x4+x3*x4

如果出现x1*x2不显著，那么可以直接删除吗？——不可以；

如果x1*x2显著，x2的系数反而不显著了，可以直接删除吗？——不可以；

正确的建模步骤是在：

1、先做无交互效应的模型：y~x1+x2+x3+x4，然后进行变量筛选；

2、剩下的变量再来考虑交互效应，若上述的四个变量全部都留下，那么再来做交互项x1*x2、x3*x4

3、如果交互项加入之后，导致原来的x1-x4四个变量有不显著的，不能删除。至于是否可以删除交互项，其实交互项若不显著和显著，都是一个非常好的结论。笔者认为交互项无论咋样，都可以不删除。

——相关结论可见谢宇老师的《回归分析》的P245页。

2、中介效应的建模

建三个模型：

y~x

x~M

y~M+x

先查看x~M,y~M系数显著性，再来判断最终的显著性。

————————————————————————————————————————————————————————

零模型的固定效应与随机效应

节选自经管之家论坛，由HLM版主提供，感谢！帖子链接

#研究者想要知道词汇成绩（gevocab）对一般阅读成绩（geread）的预测能力。
#由于学生嵌套于学校，标准的线性回归方程是不合适的。
#我们将要建立的第一个模型是零模型，即，模型中不包含自变量。
#该模型可用来估计残差和截距的变异（仅考虑嵌套于学校）。相应的lme语句见下方。

Model3.0 <- lme(fixed = geread~1, random = ~1|school, data =Achieve)

#如果仅输入Model3.0只能得到粗略的结果，我们可通过summary(Model3.0)获得计算结果。

summary(Model3.0)

#结果如下，下面这句话说明，使用的是REML算法
#Linear mixed-effects model fit by REML
#数据为Achieve 
# Data: Achieve 
#模型拟合指数
#      AIC      BIC    logLik
#  46274.31 46296.03 -23134.15
#随机效应部分
#Random effects:
# Formula: ~1 | school
#        (Intercept) Residual
#StdDev:   0.6257119  2.24611
#固定效应部分
#Fixed effects: geread ~ 1 
#               Value  Std.Error    DF t-value p-value
#(Intercept) 4.306753 0.05497501 10160 78.3402       0
#标准化的组内残差，不重要
#Standardized Within-Group Residuals:
#       Min         Q1        Med         Q3        Max 
#-2.3229469 -0.6377948 -0.2137753  0.2849664  3.8811630 
#样本量
#Number of Observations: 10320
#cluster的数量
#Number of Groups: 160 
#根据ICC的公式，ICC=二层方差/（二层方差+一层方差），结合上述随机效应部分，可计算
#ICC=0.6257119*0.6257119/(0.6257119*0.6257119+2.24611*2.24611)=0.0720157351971356