Fast Inference from Transformers via Speculative Decoding

最新推荐文章于 2025-05-18 20:34:00 发布

VvCandy_

最新推荐文章于 2025-05-18 20:34:00 发布

阅读量1.1k

点赞数 1

分类专栏： NLP大模型文章标签： python 深度学习 nlp transformer 语言模型人工智能

NLP大模型专栏收录该内容

1 篇文章

订阅专栏

有明显加速效果，但需要额外的计算资源

Abstract

像 Transformer 这样的大型自回归语言模型的推理速度非常慢，解码 K 个 token 需要连续运行模型 K 次。本文引入了 speculative decoding，通过并行计算多个 token 来更快地从自回归模型中采样，且不改变输出。

本方法的核心在于观察到：

1. 硬语言建模任务通常包含更容易地子任务，这些子任务可以通过更有效的模型很好地近似

2. 使用推测执行（speculative execution）和一种新的采样方法，在近似模型的输出上并行地运行它们，可以并发生成多个 token 而不改变分布。

这种方法可以加速现成的模型且不需要重新训练或更改架构。

Speculative Decoding

用 Mp 表示需要加速推理的目标模型，是从模型得到的前缀的分布。用 Mq 表示相同任务下的效率更高的近似模型，用表示从模型得到的前缀的分布。核心思想是：

1. 使用更高效的模型 Mq 生成补全

2. 使用目标模型 Mp 并行评估 Mq 的猜想和各自的概率，接受所有可以导致相同分布的猜想

3. 从调整后的分布中采样一个额外的 token，来修补第一个被拒绝的 token，如果所有猜想均被接受，则增加一个额外的 token

这样，目标模型 Mp 的每次并行运行都会产生至少一个新的 token。即时在最坏情况下，目标模型的串行运行次数也永远不会大于简单自回归方法。但它可能生成许多新的 token，最多 r + 1 个，具体取决于 Mq 逼近于 Mp 的程度。

Standardized Sampling

首先需要注意的是，虽然有很多采样的方法和参数（如 argmax，top-k，top-p，温度），流行的实现通常在 logits 级别上对它们做不同的处理，它们都很容易从调整后的概率分布中转换为标准采样。例如 argmax 采样等价于将分布的非 max 值变为 0 后进行规范化。

因此，我们可以只处理概率分布中的标准采样，并将所有其他类型的采样放入该框架中。接下来，我们假设 p(x) 和 q(x) 分别是 Mp 和 Mq 的分布，并根据采样方法进行调整。

Speculative Sampling

使用从分布 x~q(x) 采样替代从 x~p(x) 采样，如果 q(x) < p(x)，保留采样结果，否则，以 1-p(x)/q(x) 的概率拒绝 q(x) 的采样结果，并且从调整后的分布中重新采样 x 替代 q(x) 的采样结果。

（附录 A.1 证明，对于任意 p(x) 分布和 q(x) 分布，通过这种方式采样都等同于从 x~p(x) 采样）

给定在条件前缀（prefix）上运行 Mq 得到的分布 q(x)，可以采样到 token x1~q(x)。然后在 prefix 上运行 Mp 计算分布 p(x)，同时在 prefix + [x1] 上运行 Mp 来并行地推测下一个 token x2 的分布。

一旦两个步骤完成，就按照前面的方式继续：如果 x1 被拒绝，就不再计算 x2 而是从调整过的分布中重新采样 x1，如果 x1 被接受，就保留 x1 和 x2.

算法 1 将这一想法推广到一次采样 1~r+1 个token

Analysis

Number of Generated Tokens

定义：给定前缀，接受率表示每次 speculative sampling 得到的被接受的概率。

表示 Mq 和 Mp 近似程度的自然度量。假设独立同分布，，算法 1 运行一次生成的 token 数是一个有上限的几何变量，成功概率为 1 − α，上限为 γ + 1，算法 1 预期生成的 token 数量满足方程：

Calculating α

给定前缀和两个模型 Mp 和 Mq，如何计算 α ？

定义自然散度：

Number of Arithmetic Operations

算法 1 并行执行 Mp γ+1 次，因此，并发算术运算数量增加了 γ+1 倍。由于算法 1 每次运行最多生成 γ+1 个 token，因此算术运算总数可能高于标准解码算法。如果接受来自 Mq 的样本，操作总数不会增加，如果拒绝来自 Mq 的样本，就会产生多余的计算。

Choosing γ

给定 c 和 α ，假设有足够的计算资源，最大化 walltime improvement 方程可以得到最优 γ ，由于 γ 是整数，因此很容易通过计算得到：

推理速度和操作数之间的权衡

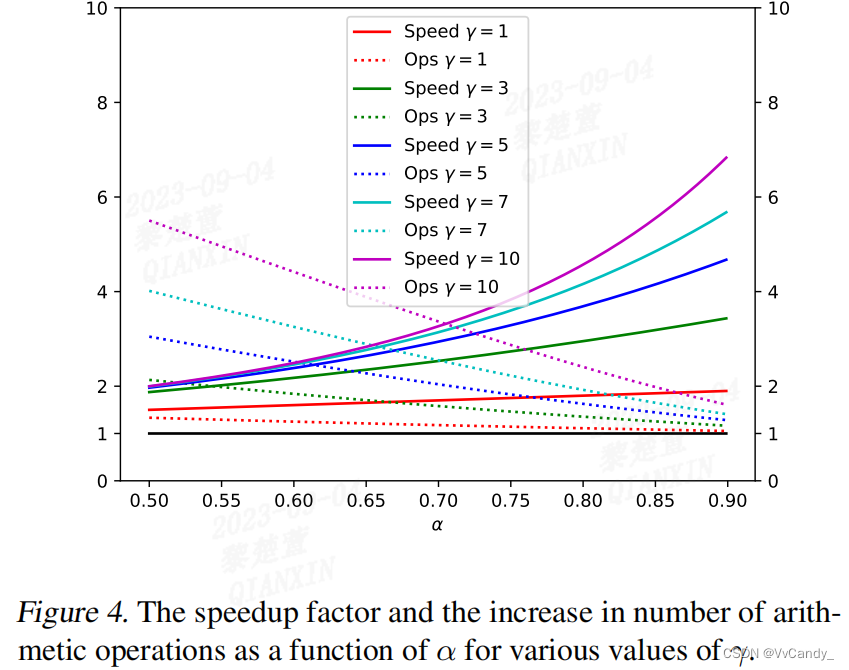
Approximation Models

推测性采样以及推测性解码可以保证任意选择的近似模型 Mq 具有相同的输出分布。本文实验主要选择了现有的小 transformer 模型作为近似模型，并且只测试了和目标模型 Mp 拥有相同结构的近似模型，使用相同的概率标准化。在这种设置下，选择比 Mp 小两个数量级的 Mq 通常效果最好，可以平衡 α 和 c

另一种近似模型，c ≈0，即相对于目标模型，可以忽略其代价。此时，理想的 walltime improvement 为，当 γ 趋于无穷大时，其上界为。n-gram 模型是该类模型之一，有趣的是，即时是 n-gram 模型，也能得到非零的 α。在英德语翻译任务中，Mp 为 11B 的 T5-XXL 模型，Mq 为简单的 bigram 模型，可以得到 α≈2，当 γ 为 3 时，图里速度提高了 1.25 倍。

Experiment

Empirical Walltime Improvement

实验设置

在 T5 论文中的两个任务上测试了标准的编-解码器 T5 1.1 版本模型

1. WMT EnDe 上微调的英语翻译德语任务

2. CCN/DM 上微调的文本摘要任务

两个任务均使用 11B 大小的 T5-XXL 模型。近似模型使用：T5-large（800M），T5-base（250M），T5-small （77M）。所有模型均使用现有的 checkpoints。对于 argmax 采样（temp=0）和标准采用（temp=1），在单个 TPU-v4 上使用批处理大小为 1 来衡量运行时间的改进情况