自适应大邻域搜索算法（Adaptive Large Neighborhood Search——ALNS）

已于 2022-04-03 16:53:52 修改
阅读量9.9k 收藏 109
点赞数 16
分类专栏： 优化算法 学习思考总结 文章标签： 人工智能 算法
于 2022-03-31 10:50:52 首次发布
原文链接：https://zhuanlan.zhihu.com/p/102298240
版权

目录 

1.邻域搜索及其大家族

1.1 邻域搜索涉及概念

1.2 邻域搜索的分类

1.3 超大邻域搜索方法VLSN

1.4 大邻域搜索方法——邻域通过destroy和repair方法隐式定义

1.4.1 自适应大邻域搜索ALNS——为每个destroy和repair方法分配一个权重

2.destroy和repair方法——邻域构建的关键

3.ALNS的具体流程

3.1 LNS的伪代码

3.2 ALNS的具体流程

这又是一种基于邻域的搜索算法，邻域及其邻域的相关知识可以看这篇——禁忌搜索（TS——Tabu Search）与邻域搜索基础知识。之所以单独拿出来，是因为邻域搜索Neighborhood Search(NS)（本质也是一种启发式算法）也是一个奇妙的分支。

自适应大邻域搜索算法(Adaptive Large Neighborhood Search)是由Ropke与Pisinger在2006年提出的一种启发式方法。它在邻域搜索的基础上增加了的对算子作用效果的衡量，使算法能够自适应选择好的算子对解进行破坏与修复，从而加速更好的解方案的产生。

在邻域搜索算法中，如果邻域搜索范围较小，那么即使使用额外的元启发式技术，如模拟退火或禁忌搜索，也很难摆脱陷入局部最优的情况；在大型邻域搜索技术中(如变邻域搜索算法)，通过在当前解的多个邻域中寻找更满意的解，能够大大提高算法在解空间的搜索范围，但是它在使用算子时盲目地将每种算子形成的邻域结构都搜索一遍，缺少了一些启发式信息的指导且时间成本较高。

自适应大邻域搜索算法弥补了这种不足，首先ALNS算法允许在一次搜索中搜索多个邻域，它会根据算子的历史表现与使用次数选择下一次迭代使用的算子，通过算子间的相互竞争来生成当前解的邻域结构，而在这种结构中有很大概率能够找到更好的解。

1.邻域搜索及其大家族

1.1 邻域搜索涉及概念

邻域搜索算法（或称为局部搜索算法）是一类非常常见的改进算法，在每次迭代时通过搜索当前解的“邻域”找到更优的解。 邻域搜索算法设计中的关键是邻域结构的选择，即邻域定义的方式。 根据以往的经验，邻域越大，局部最优解就越好，这样获得的全局最优解就越好。 但是，与此同时，邻域越大，每次迭代搜索邻域所需的时间也越长。出于这个原因，除非能够以非常有效的方式搜索较大的邻域，否则启发式搜索也得不到很好的效果。所以仍然是时间和解的质量的平衡。

所谓邻域，简单的说即是给定点附近其它点的集合。在距离空间中，邻域一般被定义为以给定点为圆心的一个圆；而在组合优化问题中，邻域一般定义为由给定转化规则对给定的问题域上每结点进行转化所得到的问题域上结点的集合 。通俗一点：邻域就是指对当前解进行一个操作(这个操作可以称之为邻域动作，也可以称为 )可以得到的所有解的集合。那么不同邻域的本质区别就在于邻域动作的不同了。

1.2 邻域搜索的分类

邻域搜索：neighborhood serach，它有好多种衍生和变种出来的算法。比如大邻域Large Neighborhood Serach，LNS；超大规模邻域搜索算法Very Large Scale Neighborhood Search，VLSNA ；或者自适应邻域搜索Adaptive Large Neighborhood Search ，ALNS。名字很相近，实则大有不同。

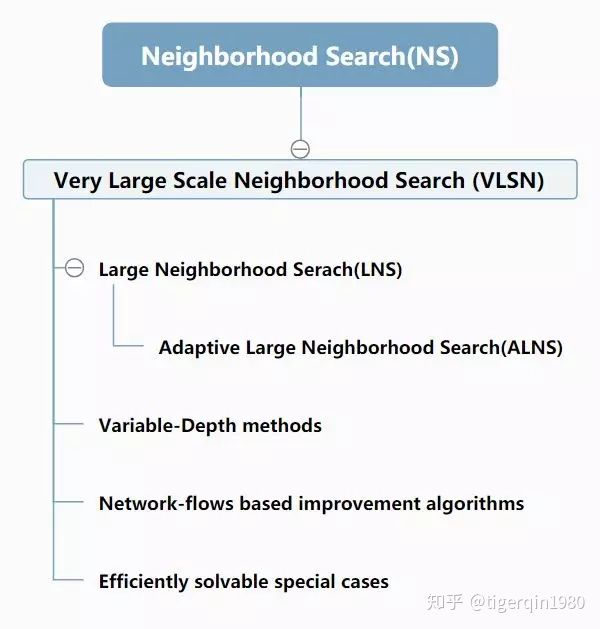
1.3 超大邻域搜索方法VLSN

当一个邻域搜索算法搜索的邻域规模随着算例规模的增大而呈指数增长，或者邻域太大而不能在实际中明确搜索时，我们把这类邻域搜索算法归类为Very Large-Scale Neighborhood Search(VLSN)。

一些超大规模的邻域搜索方法已经运用于运筹学中了，并且取得了不错的效果。 例如，如果将求解线性规划的单纯形算法看成邻域搜索算法的话，那么列生成算法就是一种超大规模的邻域搜索方法。 此外，用于解决许多网络流问题的方法也可以归类为超大规模的邻域搜索方法。 用于求解最小费用流问题的negative cost cycle canceling algorithm和用于求解分配问题的augmenting path algorithm就是两个例子。[1]

超大规模邻域搜索算法VLSN又可以分为三类：[1]

  • Variable-depth methods
  • Network-flows based improvement algorithms
  • Efficiently solvable special cases

而Large Neighborhood Search(LNS) 则不属于以上三种类型，但它确实是属于VLSN这种类型的，因为它搜索的是一个非常大的邻域。

最后呢，是Adaptive Large Neighborhood Search(ALNS)，它是根据Large Neighborhood Search(LNS) 算法扩展和延伸而来（嗯，相当于爸爸和儿子的关系……）。

1.4 大邻域搜索方法——邻域通过destroy和repair方法隐式定义

Large Neighborhood Serach，LNS，是VLSN的一个实例。大多数邻域搜索算法都明确定义它们的邻域。 在LNS中，邻域是由destroy和repair方法隐式定义的。destroy方法会破坏当前解的一部分，而后repair方法会对被破坏的解进行重建。destroy方法通常包含随机性的元素，以便在每次调用destroy方法时破坏解的不同部分。

当前解x经过destroy和repair方法以后生成的是一个邻域（邻居解的集合）。

那么，解x的邻域N（x）就可以定义为：首先通过利用destroy方法破坏解x，然后利用repair方法重建解x，从而得到的一系列解的集合（邻域）。

1.4.1 自适应大邻域搜索ALNS——为每个destroy和repair方法分配一个权重

ALNS是从LNS发展扩展而来的，在了解了LNS以后，我们现在来看看ALNS。ALNS在LSN的基础上，允许在同一个搜索中使用多个destroy和repair方法来获得当前解的邻域。

ALNS会为每个destroy和repair方法分配一个权重，通过该权重从而控制每个destroy和repair方法在搜索期间使用的频率。 在搜索的过程中，ALNS会对各个destroy和repair方法的权重进行动态调整，以便获得更好的邻域和解。

简单点解释，ALNS和LNS不同的是，ALNS通过使用多种destroy和repair方法，然后再根据这些destroy和repair方法生成的解的质量，选择那些表现好的destroy和repair方法，再次生成邻域进行搜索。

2.destroy和repair方法——邻域构建的关键

关于destroy和repair方法，在LNS和ALNS中是要组合在一起使用的。其实，一个解x经过destroy和repair方法以后，实则是相当于经过了一个邻域动作的变换。如下图所示：[1]

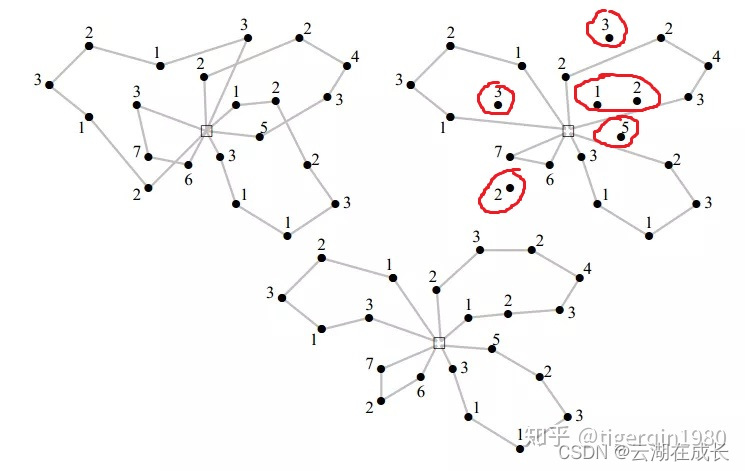
上图是三个CVRP问题的解，上左表示的是当前解，上右则是经过了destroy方法以后的解（移除了6个customers），下面表示由上右的解经过repair方法以后最终形成的解（重新插入了一些customers）。

上面展示的只是生成邻域中一个解的过程而已，实际整个邻域还有很多其他可能的解。比如在一个CVRP问题中，将destroy方法定义为：移除当前解x中15%的customers。假如当前的解x中有100名customers，那么就有C（100,15）= 100!/(15!×85!) =2.5×10的17次方 种移除的方式。并且，根据每一种移除方式，又可以有很多种修复的方法。这样下来，一对destroy和repair方法能生成非常多的邻居解，而这些邻居解的集合，就是邻域了。

3.ALNS的具体流程

3.1 LNS的伪代码

ALNS是由LNS扩展而来的，在了解ALNS之前，先来了解一下LNS的具体流程。下面是LNS的伪代码：[1]

LNS算法中包含三个变量。变量x^b记录目前为止获得的最优解，x则表示当前解，而x^t是临时解（便于回退到之前解的状态）。

函数d(.)是destroy方法，而r(.)是repair方法。详细点就是，d(x)表示破坏解x的部分，而r(x)则表示对破坏的解进行重新修复。

在第2行中，初始化了全局最优解。在第4行中，算法首先用destroy方法，然后再用repair方法来获得临时解x^t 。在第5行中，评估临时解x^t 的好坏，并以此确定该临时解x^t 是否应该成为当前新的解x（第6行）。

评估的方式因具体程序而异，可以有很多种。最简单的评估方式就只接受那些变得更优的解。注：评估准则可以参考模拟退火的算法原理，设置一个接受的可能性，效果也许会更佳。

第8行检查新解x是否优于全局最优解x^(b)。此处c(x)表示解x的目标函数值。如果新获得的解x更优，那么第9行将会更新全局最优解x^(b)。在第11行中，检查终止条件。在第12行中，返回找到的全局最优解x^(b)。

从伪代码可以注意到，LNS算法不会搜索解的整个邻域，而只是对该邻域进行采样搜索。也就是说，这么大的邻域是不可能一一遍历搜索的，只能采样，搜索其中的一些解而已。

3.2 ALNS的具体流程

在理解了LNS的基础上，理解ALNS也非常easy了。前面说过，ALNS对LNS进行了扩展，它允许在一次搜索中搜索多个邻域（使用多组不同的destroy和repair方法）。至于搜索哪个邻域呢，ALNS会根据邻域解的质量好坏，动态进行选择调整。好啦，来看伪代码：[1]

上面就是ALNS伪代码。相对于LNS来说，新增了第4行和第12行，修改了第2行。

\Omega ^{^{-}}和\Omega ^{^{+}}分别表示destroy和repair方法的集合。第2行中的 \rho^{-} 和  \rho ^{+}分别表示各个destroy和repair方法的权重集合。一开始时，所有的方法都设置相同的权重。

第4行根据\rho^{-}和  \rho ^{+}选择destroy和repair方法。至于选择哪个方法的可能性大小，是由下面公式算出的：[1]

总的来说，权重越大，被选中的可能性越大。

除此之外，权重大小是根据destroy和repair方法的在搜索过程中的表现进行动态调整的（第12行）。具体是怎么调整的呢？这里也给大家说一说：

在ALNS完成一次迭代搜索以后，我们使用下面的函数为每组destroy和repair方法的好坏进行一个评估：[1]

其中，  \omega_{1}\geq \omega _{2}\geq \omega _{3}\geq \omega _{4}\geq0，为自定的参数。

假如，a和b是上次迭代中使用的destroy和repair方法。那么其权重更新如下所示：

其中，λ∈[0,1]，为参数。

再来给大家看个图

在一个ALNS算法中，有很多个邻域，每个邻域都可以看做是一组destroy和repair方法生成的。

参考链接：

干货 | 自适应大邻域搜索入门到精通超详细解析-概念篇 - 知乎

云湖在成长
关注
  • 16
    点赞
  • 踩
  • 109
    收藏
    觉得还不错? 一键收藏
  • 3
    评论
专栏目录
代码 | 自适应大邻域搜索系列之(6) - 判断接受准则SimulatedAnnealing的代码解析
infinitor的博客
05-10 460
代码 | 自适应大邻域搜索系列之(6) - 判断接受准则SimulatedAnnealing的代码解析 前言 前面三篇文章对大家来说应该很简单吧？不过轻松了这么久，今天再来看点刺激的。关于判断接受准则的代码。其实，判断接受准则有很多种，效果也因代码而异。今天介绍的是模拟退火的判断接受准则。那么，相关的原理之前的推文有讲过，不懂的同学回去翻翻这个文章...
代码 | 自适应大邻域搜索系列之(2) - ALNS算法主逻辑结构解析
infinitor的博客
03-23 3190
00 前言 在上一篇推文中，教大家利用了ALNS的lib库求解了一个TSP问题作为实例。不知道你萌把代码跑起来了没有。那么，今天咱们再接再厉。跑完代码以后，小编再给大家深入讲解具体的代码内容。大家快去搬个小板凳一起过来围观学习吧~ 01 总体概述 前排高能预警，在下面的讲解中，会涉及很多C++语言的知识，特别是类与派生这一块的内容，如果C++基础比较薄弱的同学则需要回去（洗洗睡）再好好补一补啦，在...
ALNS-VRPPD（Python）自适应大邻域搜索解决取送货的VRP问题（Python）
05-13
1、完整代码，可直接运行 （如有疑问可私信） 2、擅长领域：路径规划、机器学习、数据爬虫、数据分析处理等 3、该资源有较为详尽的注解，非常方便大家阅读与理解。 ALNS_VRPPD（Python） 自适应大邻域搜索解决取送货的VRP问题（Python）
自适应大规模邻域算法(ALNS)解决VRPTW问题(JAVA)
Made-In-China-0711的博客
03-31 5182
本文介绍了一种启发式算法（ALNS）的Java代码，并用该算法求解了VRPTW问题实例（SolomnC101（100）算例）。结果显示算法的运行时间在可接受范围内。
探索邻域：Neighbor - 最近邻搜索库的神器
最新发布
gitblog_00071的博客
05-24 259
探索邻域：Neighbor - 最近邻搜索库的神器 项目地址:https://gitcode.com/ankane/neighbor 项目介绍 在数据密集型应用中，快速和精确的最近邻搜索是提高用户体验的关键。Neighbor 是一个专为 Ruby on Rails 和 PostgreSQL 设计的开源库，它提供了强大的立方体（cube）和向量（vector）扩展，帮助您轻松实现高效的数据相似性搜索...
【运筹优化】元启发式算法详解：(自适应)大邻域搜索算法（( Adaptive) Large Neighborhood Search，(A)LNS）+ 案例讲解&代码实现
知不足而奋进，望远山而前行
06-12 6440
在过去的15年中，基于大邻域搜索(LNS)和变异自适应大邻域搜索(ALNS)的启发式算法已经成为解决各种运输和调度问题的一些最成功的范例。大邻域搜索方法通过使用试探法来探索复杂的邻域（交替地破坏和修复解来逐渐改进初始解）。使用大邻域使得在每次迭代中找到更好的候选解成为可能，并因此遵循更有希望的搜索路径。本博客从大邻域搜索的一般框架出发，深入研究了自适应大邻域搜索，讨论了该框架的设计思想和性质。讨论了大邻域搜索方法在路由和调度中的应用。
自适应大邻域搜索(Adaptive Large Neighborhood Search)-详解
sky的博客
09-06 3629
一、概念
禁忌搜索（TS——Tabu Search）与邻域搜索基础知识
sinat_41348401的博客
03-28 8775
禁忌搜索，也是一种常见的邻域搜索算法。其实我觉得很多智能算法本质都是邻域搜索（本质是局部搜索）算法。只不过邻域的应用方式不同，是全局式的邻域搜索算法。比如，局部搜索中最经典的是“爬山算法”。但是会陷入局部最优。 禁忌搜索，比较适合解决大规模问题。本质思想是，在极值附近设置禁忌（暂时不许进入）的标识，以达到多多的遍历可行域，保证种群多样性的目的。由美国科罗拉多大学教授Fred Glover在1986年左右提出的，是一个用来跳脱局部最优解的搜索方法。其先创立一个初始化的方案；基于此，算法“移动”到一相邻的
自适应大领域搜索算法
再来一下！
07-20 414
概念理解干货 | 自适应大邻域搜索(Adaptive Large Neighborhood Search)入门到精通超详细解析-概念篇优点、步骤和python示例代码自适应大邻域搜索算法参考文献及算法应用[1]王新. 车辆和无人机联合配送路径问题研究[D].大连海事大学,2020.[2]李婷玉. 多商户多车程同城物流配送车辆调度问题研究[D].大连理工大学,2018.[3]张梦颖. 不确定因素下路径规划问题研究[D].中国科学技术大学,2016.破坏解修复解动态调整权重并选择（自适应）。
【进阶一】Python实现MDCVRP常见求解算法——自适应大邻域搜索算法（ALNS）
Better.C的博客
09-16 3553
基于python语言，实现自适应大邻域搜索算法（ALNS）对多车场车辆路径规划问题（MDCVRP）进行求解。
求解VRPTW的自适应大规模领域搜索算法
#Amark的博客
09-02 1813
最近在做一个基于物流配送的路径规划的问题，才了解到这个算法，也算是在做一个算法的入门吧。 智能配送计划本质是车辆路径规划（VRP）问题，是运筹中的经典问题。 是指一定数量的客户，各自有不同数量需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线 目标：路程最短最小、成本最小、耗费时间最少，使用的车辆数 约束：车辆载重、车辆满载限制、时间窗口、车辆服务客户数、车辆行驶的距离、最大可用车辆数等 决策变量：车辆行驶路径 算法主要设计两个大类 设计算法的大概思路 数...
ALNS:Python中的自适应大邻域搜索
05-04
基于的描述，此程序包提供了自适应大邻域搜索（ALNS）元启发式方法的一般，经过充分记录和测试的实现。 它可以按以下常规方式安装： pip install alns 如何使用 alns包提供了两个类，即ALNS和State 。 第一个可以用来运行ALNS算法，第二个可以被子类化以存储解决方案状态-它所需要的只是定义一个objective成员函数，并返回一个目标值。 必须为ALNS算法提供接受标准，以便在每次迭代时确定是否接受新的解决方案状态。 给出了通用验收标准的概述 。 在alns.criteria ，已经为您实现了几个 HillClimbing 。 最简单的接受标准是爬山，仅接受提高目标值的解决方案。 RecordToRecordTravel 。 仅当改进满足某些更新阈值时，此准则才接受解决方案。 SimulatedAnnealing 。 当标度概率大于某个随机数时，使用更新温
Python实现自适应大邻域搜索算法解决TSP问题
04-30
Python实现自适应大邻域搜索算法解决TSP问题。 该TSP解决的是这样一个问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。
最近邻域分类法matlab实现
06-11
最简单的模式识别分类器，最小邻域分类，分类速度快，小样本时识别率高，matlab版本。
自适应大邻域搜索算法ALNS附Python代码.zip
11-11
4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。 5.作者介绍：某大厂资深算法工程师，从事Matlab算法仿真工作10年；擅长智能优化算法、神经网络预测、信号处理、元胞...
一种基于强化学习的自适应多邻域人工蜂群算法
04-19
一种基于强化学习的自适应多邻域人工蜂群算法是一种优化算法，结合了强化学习和人工蜂群算法的思想。该算法通过引入强化学习的机制，使得人工蜂群算法能够在不同问题和环境下进行自适应调整和优化。
ALNS自适应大规模邻域搜索算法核心
m0_62281625的博客
03-14 1260
LNS（Large Neighborhood Search）是一种，用于解决组合优化问题。它是基于局部搜索的思想，但与传统的局部搜索算法不同，LNS通过在搜索过程中采用大规模变动来跳出局部最优解，并在此基础上进行小规模搜索以逐步改进当前解。其核心是破坏算子和修复算子，如何选择和构建破坏算子和修复算子是较为关键的一部分，文献中大部分学者的做法是通过设计多个算子，通过不同得分进而用轮盘赌的选择方法选择适合的算子，以此文献为例。
提高邻域搜索效率
qq_39289735的博客
11-28 788
分享学术大牛vidal在解决CVRP（Capacitated vehicle routing problem）问题时通过改进解的表示以及搜索框架两个方面提升邻域搜索效率的方法。
[大邻域算法](MD)VRPTW常见求解算法--代码解析
panbaoran913的博客
02-17 1712
文章代码的解析篇
用python写自适应大邻域算法
05-25
自适应大邻域算法（Adaptive Large Neighborhood Search，ALNS）是一种启发式算法，用于解决组合优化问题。它通过动态调整邻域结构，以达到更好的搜索效果。 以下是一个用Python实现ALNS算法的示例： ```python import random class Solution: def __init__(self, n): self.n = n self.seq = list(range(1, n+1)) random.shuffle(self.seq) self.cost = self.evaluate() def evaluate(self): # 计算当前解的成本 cost = 0 for i in range(self.n-1): for j in range(i+1, self.n): if abs(i-j) == abs(self.seq[i]-self.seq[j]): cost += 1 return cost def get_neighbor(self): # 生成一个随机邻居 i, j = random.sample(range(self.n), 2) seq = self.seq.copy() seq[i], seq[j] = seq[j], seq[i] return Solution.from_seq(seq) def apply_move(self, move): # 应用一个移动操作 i, j = move self.seq[i], self.seq[j] = self.seq[j], self.seq[i] self.cost = self.evaluate() @classmethod def from_seq(cls, seq): # 从序列创建一个解 instance = cls(len(seq)) instance.seq = seq instance.cost = instance.evaluate() return instance class ALNS: def __init__(self, problem, max_iter=1000, p_init=0.9, p_decay=0.99, max_tabu_size=10): self.problem = problem self.max_iter = max_iter self.p_init = p_init self.p_decay = p_decay self.max_tabu_size = max_tabu_size self.tabu_list = [] def run(self): curr = self.problem best = curr p = self.p_init for i in range(self.max_iter): neighbor = curr.get_neighbor() if neighbor.cost < curr.cost or random.random() < p: curr = neighbor if curr.cost < best.cost: best = curr self.update_tabu_list(curr, neighbor) p *= self.p_decay return best def update_tabu_list(self, curr, neighbor): # 更新禁忌表 move = self.get_move(curr, neighbor) if move in self.tabu_list: self.tabu_list.remove(move) self.tabu_list.append(move) if len(self.tabu_list) > self.max_tabu_size: self.tabu_list.pop(0) def get_move(self, curr, neighbor): # 获取当前解到邻居解的移动操作 for i in range(curr.n): if curr.seq[i] != neighbor.seq[i]: for j in range(i+1, curr.n): if curr.seq[j] != neighbor.seq[j] and (i, j) not in self.tabu_list: return (i, j) ``` 在这个示例中，我们定义了一个`Solution`类来表示一个解。`Solution`类有一个`seq`属性表示解的序列，一个`cost`属性表示解的成本。`Solution`类还有一个`evaluate`方法来计算解的成本，一个`get_neighbor`方法来生成一个随机邻居，一个`apply_move`方法来将一个移动操作应用到当前解上。`Solution`类还有一个`from_seq`类方法来从序列创建一个解。 我们还定义了一个`ALNS`类来实现ALNS算法。`ALNS`类有一个`run`方法来运行算法，一个`update_tabu_list`方法来更新禁忌表，一个`get_move`方法来获取当前解到邻居解的移动操作。 在`run`方法中，我们首先初始化当前解和最佳解为问题的初始解。然后在循环中，我们生成一个随机邻居，并根据概率和成本比较决定是否接受该邻居。如果接受该邻居，则更新当前解和禁忌表，并更新最佳解。最后，我们通过逐步减小概率`p`来控制算法的收敛性。 这个示例实现了一个简单的N皇后问题，但可以通过修改`Solution`类和`ALNS`类来适应其他组合优化问题。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值