【转】二维异形件排版算法介绍（三）

转自：https://bbs.huaweicloud.com/blogs/203947

【摘要】 相比于基于可行解的排样算法，重叠移除算法在改变解的状态时，允许零件之间发生重叠，然后采用分离技术消除重叠，直到达到算法的终止条件为止。重叠移除算法的关键技术点主要有：重叠度量方法、零件扰动技术、重叠消除技术。

1       二维异形件排样算法

上两篇博客提到二维异形件排样算法涉及到临界多边形（NFP）的求解算法，以及排样算法的排样策略，感兴趣的童鞋可以查看博文：          https://bbs.huaweicloud.com/blogs/175385

https://bbs.huaweicloud.com/blogs/196289

2       二维异形件重叠移除排样算法

 

相比于基于可行解的排样算法，重叠移除算法在改变解的状态时，允许零件之间发生重叠，然后采用分离技术消除重叠，直到达到算法的终止条件为止。重叠移除算法的基本流程伪代码如下图所示：

 

图1. 重叠移除算法基本流程伪代码（图片来源：参考文献[1]）

其中，MinimizeOverlap函数是重叠移除算法的关键，涉及到的关键技术点主要有：重叠度量方法、零件扰动技术、重叠消除技术。下面分别就这三个方面进行简要介绍。

 

2.1   重叠度量方法

两个零件之间的重叠指标主要有三种方式，如图2所示，分别是重叠面积、最小嵌入深度，以及最小横向/纵向嵌入深度等。重叠面积是最直接的衡量零件重叠的方法，但是此种方法最大的问题是计算复杂度高，每移动一次零件，都要求计算其与其他零件的重叠面积。第2种重叠衡量方法是最小嵌入深度。所谓嵌入深度，是指为消除重叠，按照某个方向移动其中一个零件的距离。所谓最小嵌入深度，是指所有可能方向的嵌入深度的最小值。第3种重叠移除方法是第2种方法的特例，限制可能方向为横向和纵向两种。

 

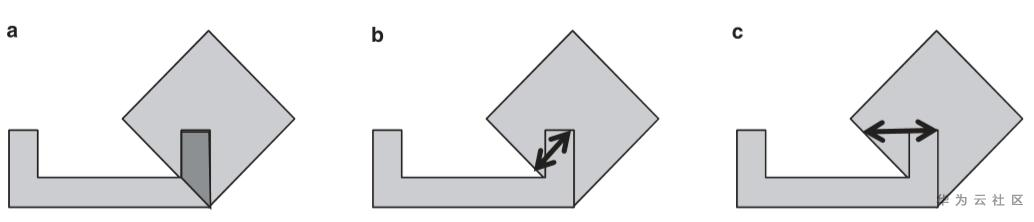
图2. 重叠指标计算方法：(a) 重叠面积；(b) 最小嵌入深度；(c) 最小横向/纵向嵌入深度

 

 

重叠移除算法的一个主要瓶颈是计算量大，其中，零件重叠度量是其中主要瓶颈之一。为提高算法效率，学术界提出了很多种改进算法[2,3,4]。以第2种方法为例，直接的思路是计算参考点相对于NFP每条边的最小距离，从中选择最小值即为最小嵌入深度。这个方法的时间复杂度是O(n)，其中n表示NFP的边个数。为简化计算，可采用Medial Axis算法对NFP进行剖分，当参考点落在其中某个剖分时，参考点到该剖分对应线段的最小距离即为该点到NFP所有线段的最小值。如图3所示，当参考点为v1时，其到线段s3的最小距离即为该点到NFP所有线段的最小距离。

 

图3. NFP的Medial Axis剖分（图片来源：参考文献[3]）

2.2   零件扰动技术

零件扰动技术主要包括三大类：平移、旋转和交换[5]。扰动的目的是破坏当前的解结构，使零件之间产生重叠，以便使用重叠移除技术消除之。从优化的角度分析，零件扰动是为了跳出当前的局部最优解，向更优解进发的必要步骤。

2.3 重叠移除技术

 

重叠移除技术主要有两种策略：每次移动所有零件和每次移动一个零件。分别介绍如下：

（1）每次移动所有样片

以文献[3]中的基于非线性优化算法（LBFGS）的重叠移除方案为例，该算法使用重叠零件间的嵌入深度衡量重叠程度，以当前排样方案中所有零件间嵌入深度的加和作为优化目标，将消除重叠转化为一个连续优化问题进行求解。如图4所示，该算法将消除零件间重叠所需的最小位移定义为梯度函数，在梯度信息指导下进行零件的移动。相较于其他基于重叠移除策略的排样算法，该算法的局部寻优能力更强，但也更容易陷入局部病态解导致消除重叠失败。

 

图4. 零件间嵌入深度与最小分离向量

（2）每次移动一个样片

该算法每次只移动一个重叠零件。若移动后重叠指标变小，则保留此次移动，否则不进行移动。此方法主要涉及候选位置寻找算法和全局寻优算法。零件候选位置的选择通常有两种方法：一种是依次按照长度方向和宽度方向移动零件，直到零件重叠指标最小为止[4]。如图5所示，重叠零件通过3次移动最终寻找到了不发生重叠的位置；另一种是采用搜索算法，比如布谷鸟邻域搜索算法，迭代寻找重叠指标最小的点[1]。全局寻优算法一般采用Guide Local Search(GLS)算法，每次迭代后通过更新惩罚因子跳出局部最优[1,4]。

 

图5. 重叠零件候选位置寻找算法

3  总结

 

重叠移除算法原理简单，但要想实现一个高效可行的解决方案却并不容易。面临的主要难点主要有三点：

（1）  高效的计算几何算法：其中，NFP计算是首先需要攻克的难题之一；

（2）  高超的编程实现能力：重叠移除算法有部分功能函数是高频调用函数，实现细节对算法效率影响较大，一般情况需要持续优化；此外，所有的商用排版软件都采用了并行化实现方式，并行化实现方案对算法效率和效果影响也较大；、

（3）   参数调节：学术界对异形件排版算法的细节往往很少或没有介绍，这导致复现的算法几乎都达不到论文中呈现的结果，因此需要实现者自己调整算法参数，或者提出全新的改进方案。

   至此，二维异形件排版算法介绍完毕。若有问题，欢迎大家留言交流。

 

 

参考文献

 

[1] Elkeran A. A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering[J]. European Journal of Operational Research, 2013, 231(3): 757-769.

[2] Egeblad J, Nielsen B K, Odgaard A. Fast neighborhood search for two-and three-dimensional nesting problems[J]. European Journal of Operational Research, 2007, 183(3): 1249-1266.

[3] Imamichi T, Yagiura M, Nagamochi H. An iterated local search algorithm based on nonlinear programming for the irregular strip packing problem[J]. Discrete Optimization, 2009, 6(4): 345-361.

[4] Umetani S, Yagiura M, Imahori S, et al. Solving the irregular strip packing problem via guided local search for overlap minimization[J]. International Transactions in Operational Research, 2009, 16(6): 661-683.

[5] Heckmann R, Lengauer T. A simulated annealing approach to the nesting problem in the textile manufacturing industry[J]. Annals of Operations Research, 1995, 57(1): 103-133.

登录后可下载附件，请登录或者注册

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区），文章链接，文章作者等基本信息，否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件至：huaweicloud.bbs@huawei.com进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容。