一. PPL评测
大模型推理:
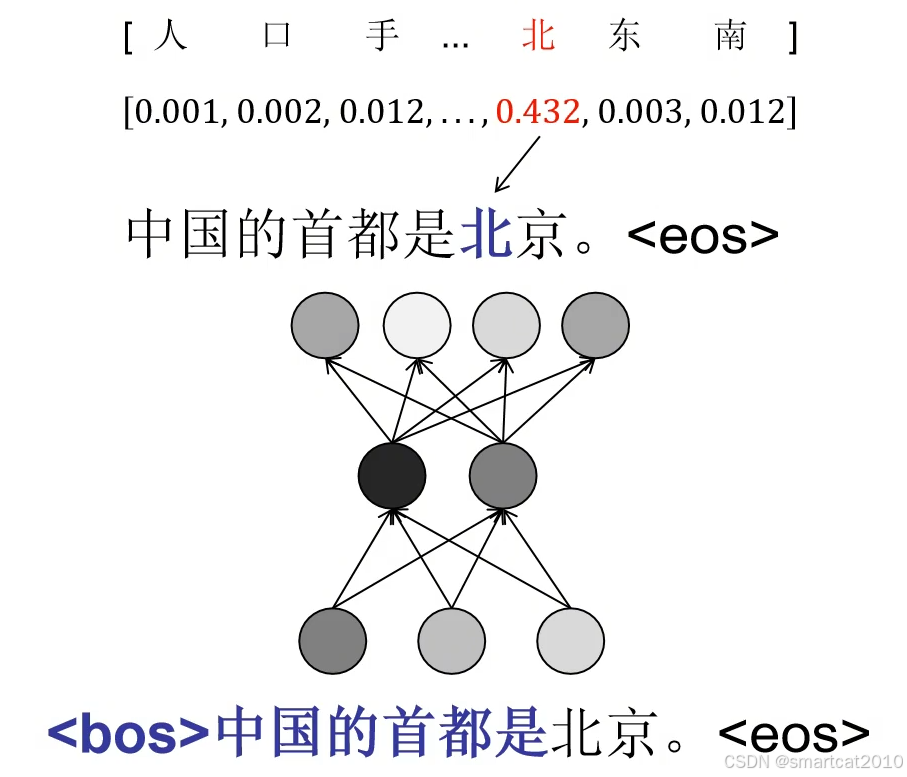
forward时,计算每一个token的生成概率:
整个句子,所有N个token的概率相乘,再开N次方,可视为每个token的“平均概率”,越大越好(“确信度”);
再求倒数,即为困惑度perplexity(PPL),越小越好。
(可以视为,生成这个句子的可能性,相当于从PPL个选项里蒙对的可能性,越小表示越确定)
上例,大模型1和大模型2,“是”之前的token,概率相差不大,“北“、”京“的概率,明显看出2个大模型的能力差异了!模型2看来是不懂这条知识的。
连乘:联合概率。开N次方:为了让“平均”概率不受句子长度的影响。
痛点:计算的时候,连乘的话,数值太小,精度不够了。
解决:使用log,先求对数再求指数:
局限性:
只能反映模型是否“倾向”被测文本。如果被测文本本身质量很烂,而大模型能力很好,则PPL是高的。例如大模型是擅长高质量写作,但被测文本是一段小孩子作文,则PPL很高。
二、人工评测
人工给大模型的输出进行打分。
或者人工给多个大模型的输出(打乱顺序,盲评,标注员不知道各自是哪个模型产生的)进行打分、胜负比较。
缺点:1. 耗费人力。2.每个标注员的主观影响,个人喜好。
三、可解析的评测集
1. 选择题。只让大模型生成选项字母(A、B、C、D)。
2. 主观题。让大模型以某种便于代码解析的格式输出,例如规定的json格式。
常用评测集:
例子:(4个选项的选择题)
例子:(10个答案选项)
例子:(可用代码来验证模型输出文字的格式是否正确)
例子:(Hard难度的题目)
例子:
GPQA是专家级题目,专业博士也只能作对65%。
评测结果:
四、大模型做裁判
适合没有固定答案的主观题,例如写诗。
把2个模型的输出结果,交给另一个大模型来判断胜负。
注意:有的大模型倾向选择前面的选项。因此要实现把选项顺序打乱。







































 1044
1044

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








