「NOI2018」情报中心（线段树合并）（虚树）

传送门

神题一道
题意：
一棵树，有边权，$m$ 条路径，路径有代价，选择两条相交的路径使得路径的并的边权 - 总代价最大
$n\le 5e4,m\le 1e5,\sum n\le 1e6,\sum m\le 2e6,8s$

直接考虑 $S_1,S_2$ 的性质

$S_1$：
路径的 $lca$ 两两不同，于是路径的交只有可能是直上直下

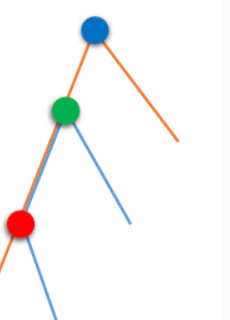
我们枚举红点，那么这个时候的贡献应该是
$le{n}_1+le{n}_2-cos{t}_1-cos{t}_2-(de{p}_R-max(de{p}_G,de{p}_B))$
考虑树上差分后线段树合并，合并的时候考虑两个不同子树路径的拼接
现在的问题就是处理哪个在上面有点烦
发现可以按深度维护线段树，维护 $len-cost$ 和 $len-cost+dep$ 的最大值
线段树合并的时候考虑一个的左子树有一个右子树拼接，就可以很巧妙地知道谁在上方
复杂度 $O((M+N)log(N))$

$S_2$

最后的贡献是：
$\frac{1}{2}(le{n}_a+le{n}_b-2\ast cos{t}_a-2\ast cos{t}_b+de{p}_a+de{p}_b-de{p}_{lca(a,b)}+dis(p_a,p_b))$
我们枚举 $lca(a,b)$ 发现除 $dis(p_a,p_b)$ 外 $a,b$ 独立
如果我们令 $p_a$ 的点权为 $le{n}_a-2\ast cos{t}_a+de{p}_a$ 的话，那么问题就是找一对最远点
现在的问题就是支持集合合并，合并的时候询问最远点
合并后的最远点一定是两个集合四个最远点的其中两个，于是可以很方便维护
对于所有路径的 $lca$ 不在一个点时，把路径存在 $lca$ 处然后大力建虚树就可以了
复杂度 $O(Mlog(N))$

---

两种方法都有很巧妙的地方
第一种是考虑线段树合并的时候更新答案就可以知道谁的深度更深
第二种是将问题转换为最远点对，对于一个点集的最远点对只需要维护两个点并支持快速合并

#include<bits/stdc++.h>
#define cs const
#define mp make_pair
using namespace std;
typedef long long ll;
cs ll INF = 1e18;
void Mx(ll &a, ll b){ if(a < b) a = b; }
int read(){
	int cnt = 0, f = 1; char ch = 0;
	while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1; }
	while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
	return cnt * f;
}
cs int N = 1e5 + 50;
int T, n, m; ll ans = -INF;
int fi[N], nxt[N], to[N], w[N], tot;
void add(int x, int y, int z){ nxt[++tot] = fi[x], fi[x] = tot, to[tot] = y, w[tot] = z; }
int lg[N], st[N][20], in[N], sgn, dep[N]; ll d[N];
struct cp{ int u; ll w; cp(int _u = 0, ll _w = 0){u = _u, w = _w; } };
void dfs(int u, int fa){
	st[in[u] = ++sgn][0] = u; 
	for(int i = fi[u]; i; i = nxt[i]){
		int t = to[i]; if(t == fa) continue;
		dep[t] = dep[u] + 1; d[t] = d[u] + (ll)w[i];
		dfs(t, u); st[++sgn][0] = u;
	}
}
int ck(int x, int y){ return dep[x] < dep[y] ? x : y; }
int lca(int x, int y){
	int l = in[x], r = in[y];
	if(l > r) swap(l, r); 
	int d = lg[r - l + 1];
	return ck(st[l][d], st[r-(1<<d)+1][d]);
}
ll dist(int x, int y){ return d[x] + d[y] - 2 * d[lca(x, y)]; }
namespace S1{
	cs int N = ::N * 25;
	ll mx1[N], mx2[N], delta;
	int ls[N], rs[N], rt[::N], nd;
	vector<cp> G[N];
	#define mid ((l+r)>>1)
	void pushup(int x){ 
		mx1[x] = max(mx1[ls[x]], mx1[rs[x]]);
		mx2[x] = max(mx2[ls[x]], mx2[rs[x]]);
	}
	void ins(int &x, int l, int r, int p, ll v1, ll v2){
		if(!x){
			x = ++nd; ls[x] = rs[x] = 0;
			mx1[x] = mx2[x] = -INF;
		} 
		if(l == r){ Mx(mx1[x], v1); Mx(mx2[x], v2); return; }
		if(p <= mid) ins(ls[x],l,mid,p,v1,v2);
		else ins(rs[x],mid+1,r,p,v1,v2); pushup(x);
	}
	void dec(int &x, int l, int r, int p){
		if(!x) return;
		if(l == r){ x = 0; return; }
		if(p <= mid) dec(ls[x],l,mid,p);
		else dec(rs[x],mid+1,r,p);
		pushup(x);
	}
	int merge(int &x, int y, int l = 1, int r = n){
		if(!x||!y) return x|y;
		if(l == r){ Mx(mx1[x],mx1[y]); Mx(mx2[x],mx2[y]); return x; }
		ans = max(ans, mx1[ls[x]] + mx2[rs[y]] - delta);
		ans = max(ans, mx2[rs[x]] + mx1[ls[y]] - delta);
		ls[x] = merge(ls[x], ls[y], l, mid);
		rs[x] = merge(rs[x], rs[y], mid+1, r); pushup(x); return x;
	}
	void dfs(int u, int fa){
		for(int i = fi[u]; i; i = nxt[i]){
			int t = to[i]; if(t == fa) continue; dfs(t, u);
		}
		delta = d[u];
		for(int i = fi[u]; i; i = nxt[i]){
			int t = to[i]; if(t == fa) continue;
			dec(rt[t], 1, n, dep[u]);
			rt[u] = merge(rt[u], rt[t]);
		}
		for(cp v:G[u]){
			int r = 0; ins(r, 1, n, dep[v.u], v.w, v.w + d[v.u]);
			rt[u] = merge(rt[u], r);
		}
	}
	void Solve(){
		mx1[0] = mx2[0] = -INF;
		dfs(1, 0); nd = 0;
		for(int i = 1; i <= n; i++) rt[i] = 0, G[i].clear();
	}
}
namespace S2{
	struct Set{ 
		cp x, y; ll d; 
		bool operator < (cs Set &a) cs{ return d < a.d; }
	};
	Set f[N];
	struct Path{ int u, v; ll w; } ;
	vector<Path> G[N];
	int sta[N], arr[N], top, now, rt;
	bool cmp(int x, int y){ return in[x] < in[y]; }
	Set calc(cp A, cp B){
		ll di = dist(A.u, B.u) + A.w + B.w;
		ans = max(ans, di / 2 - d[now]);
		return (Set){A, B, di};
	}
	void merge(Set &A, Set &B){
		if(A.d == -INF){ A = B; B.d = -INF; return; }
		if(B.d == -INF) return;
		if(now ^ rt){
			Set P = max(calc(A.x,B.x),calc(A.x,B.y));
			P = max(P, max(calc(A.y,B.x), calc(A.y,B.y)));
			A = max(A, max(P, B));
		} B.d = -INF;
	}
	void work(cs vector<Path> &vec){
		int top = 0, sz = 0; 
		for(Path t:vec){
			arr[++sz] = t.u;
			arr[++sz] = t.v;
			cp a(t.u, d[t.v] + t.w);
			cp b(t.v, d[t.u] + t.w);
			Set x = (Set){a, a, a.w << 1}, y = (Set){b, b, b.w << 1};
			merge(f[now = t.u], y); merge(f[now = t.v], x);
		}
		sort(arr + 1, arr + sz + 1, cmp);
		sta[++top] = arr[1];
		for(int i = 2; i <= sz; i++) if(arr[i] != arr[i-1]){
			int p = arr[i], l = lca(p, sta[top]);
			while(top > 1 && dep[sta[top - 1]] >= dep[l])
			merge(f[now = sta[top - 1]], f[sta[top]]), --top;
			if(sta[top] ^ l) merge(f[now = l], f[sta[top]]), sta[top] = l;
			sta[++top] = p;
		} while(top > 1) merge(f[now = sta[top - 1]], f[sta[top]]), --top;
		f[sta[1]].d = -INF;
	}
	void Solve(){
		for(int i = 1; i <= n; i++) f[i].d = -INF;
		for(int i = 1; i <= n; i++) if(G[i].size() > 1) rt = i, work(G[i]);
		for(int i = 1; i <= n; i++) G[i].clear();
	}
}
void Clear(){
	ans = -INF;
	memset(fi, 0, sizeof(int)*(n+1)); tot = sgn = 0;	
}
void Solve(){
	n = read();
	for(int i = 1; i < n; i++){
		int x = read(), y = read(), z = read();
		add(x, y, z); add(y, x, z);
	} dep[1] = 1; dfs(1, 0);

	for(int i = 2; i <= sgn; i++) lg[i] = lg[i>>1] + 1;
	for(int j = 1; (1<<j)<=sgn; j++)
	for(int i = 1; i+(1<<j)-1 <= sgn; i++)
	st[i][j] = ck(st[i][j-1], st[i+(1<<j-1)][j-1]);
	
	m = read();
	for(int i = 1; i <= m; i++){
		int u = read(), v = read(); ll w; scanf("%lld", &w);
		if(u == v) continue;
		int l = lca(u, v); ll dis = dist(u, v);
		if(v ^ l) S1::G[v].push_back(cp(l, dis - w));
		if(u ^ l) S1::G[u].push_back(cp(l, dis - w));
		S2::G[l].push_back((S2::Path){u, v, dis - 2 * w});
	}
	S1::Solve();
	S2::Solve();
	if(ans < -1e17) puts("F");
	else cout << ans << '\n';
}
int main(){
	freopen("center.in","r",stdin);
	freopen("center.out","w",stdout);
	T = read();
	while(T--) Solve(), Clear();
	return 0;
}