更一般情况下观察曲线的形状

虽然通过符号计算得到了某些特定参数设定下"五角星"形状曲线的参数方程,而且观察了不同参数对其形状的影响,但是,如何发现这些"形状"参数在构造类似的circle rolling on circle的动态曲线时的具体设定和形状之间的规律,就成为一个还不直观的反问题.

于是

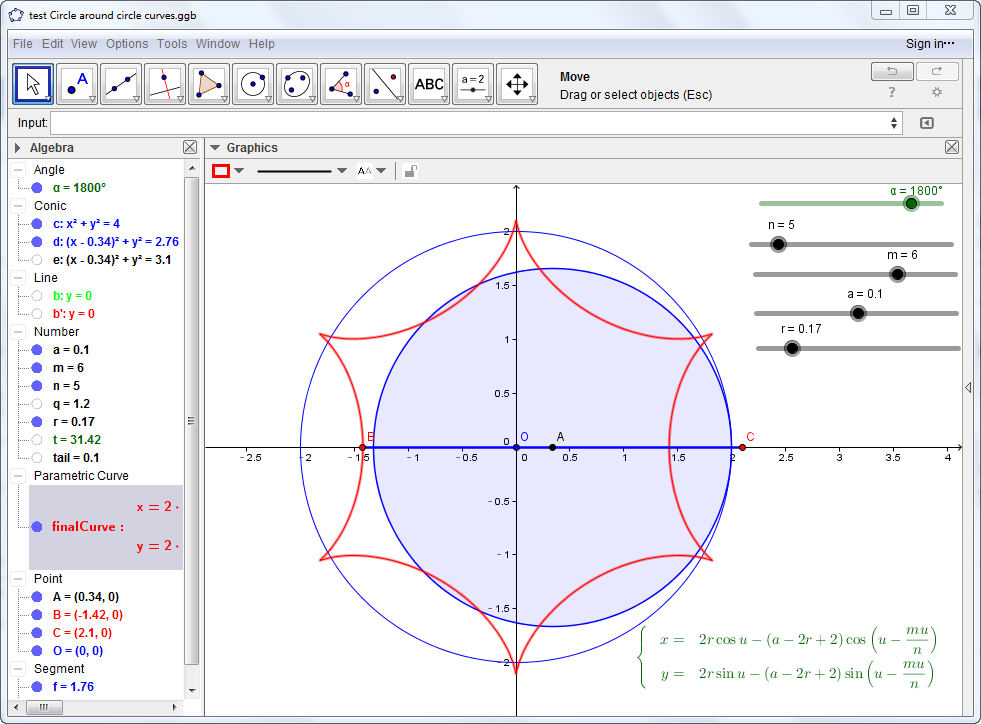
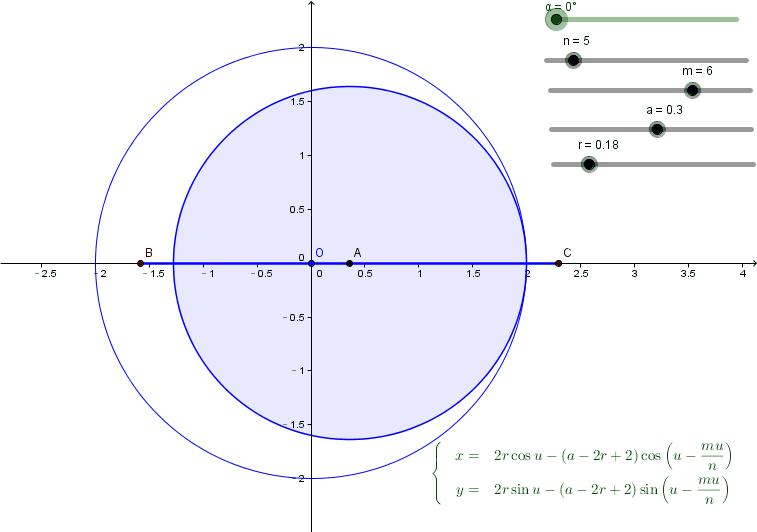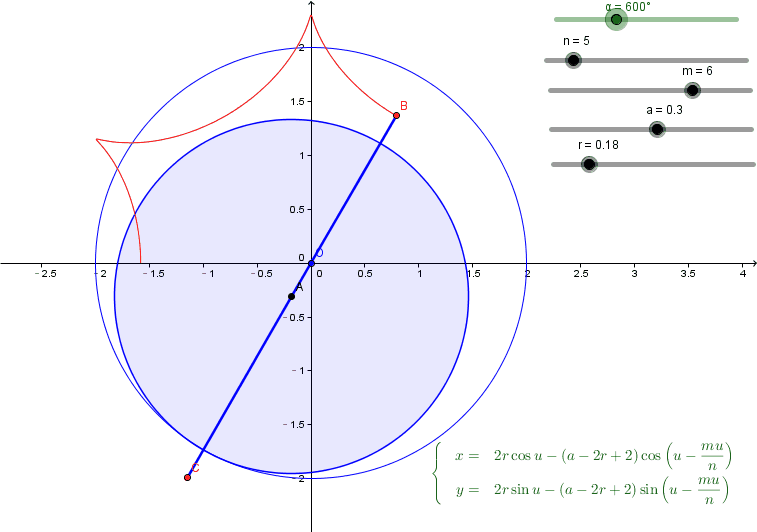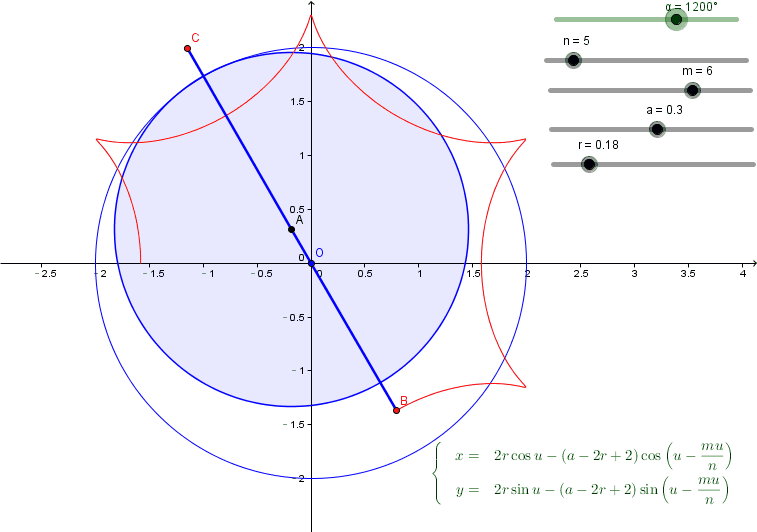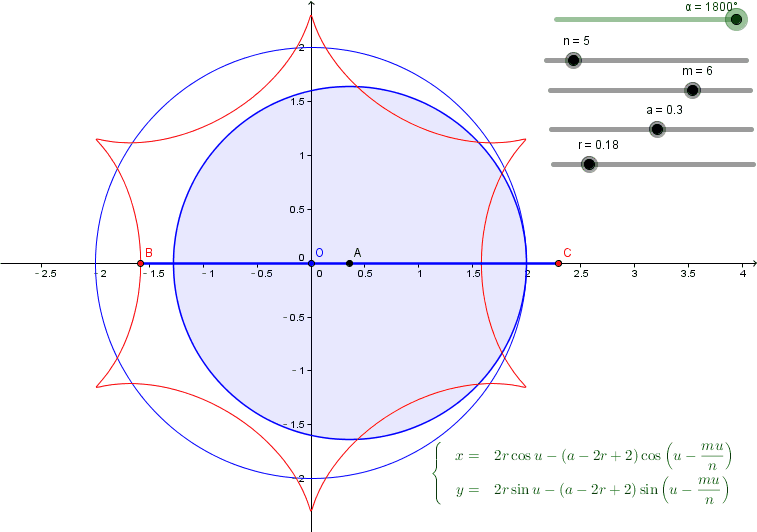
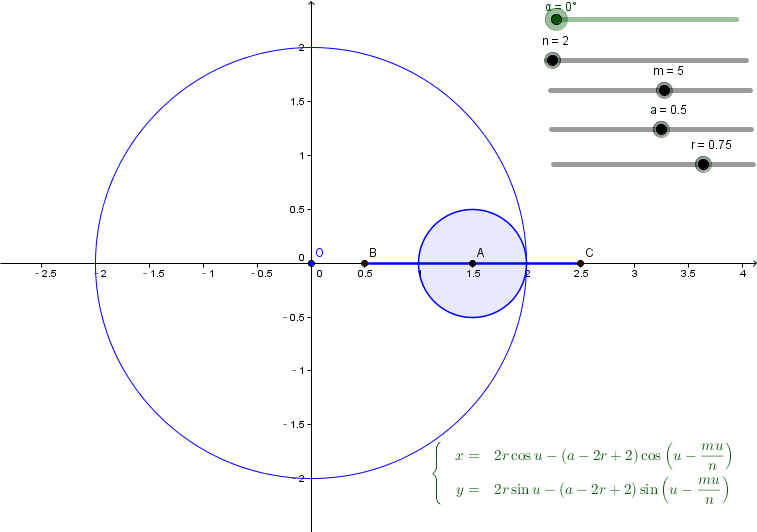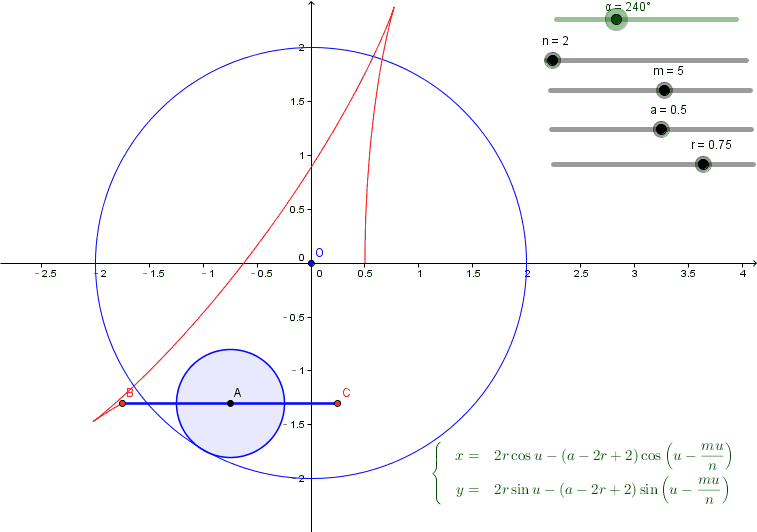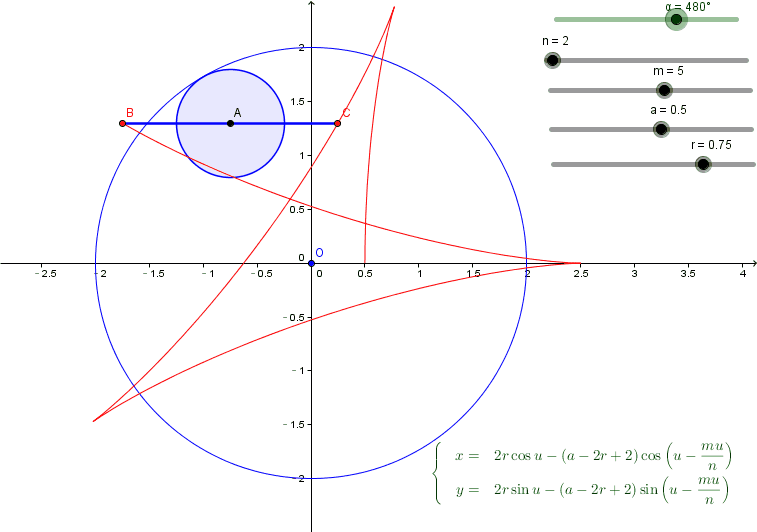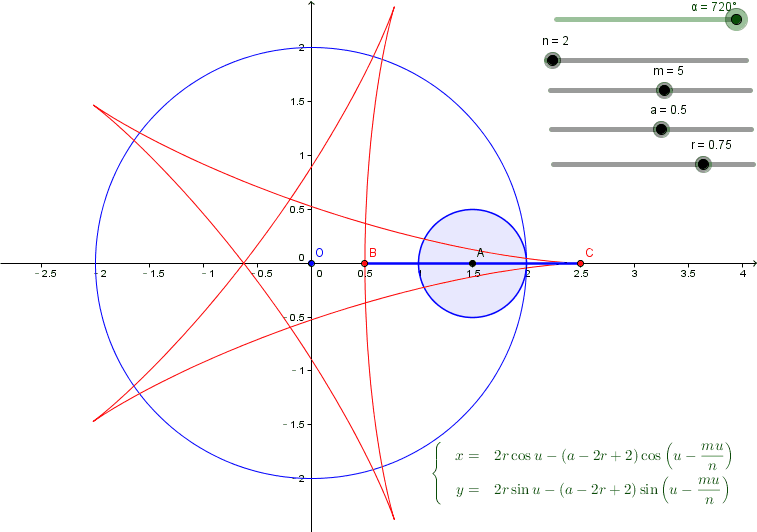
(1)把可能的参数都变成slider放在Geogebra中,如图所示;

(2)符号的方式得到最终可能曲线的参数方程, 图中右下

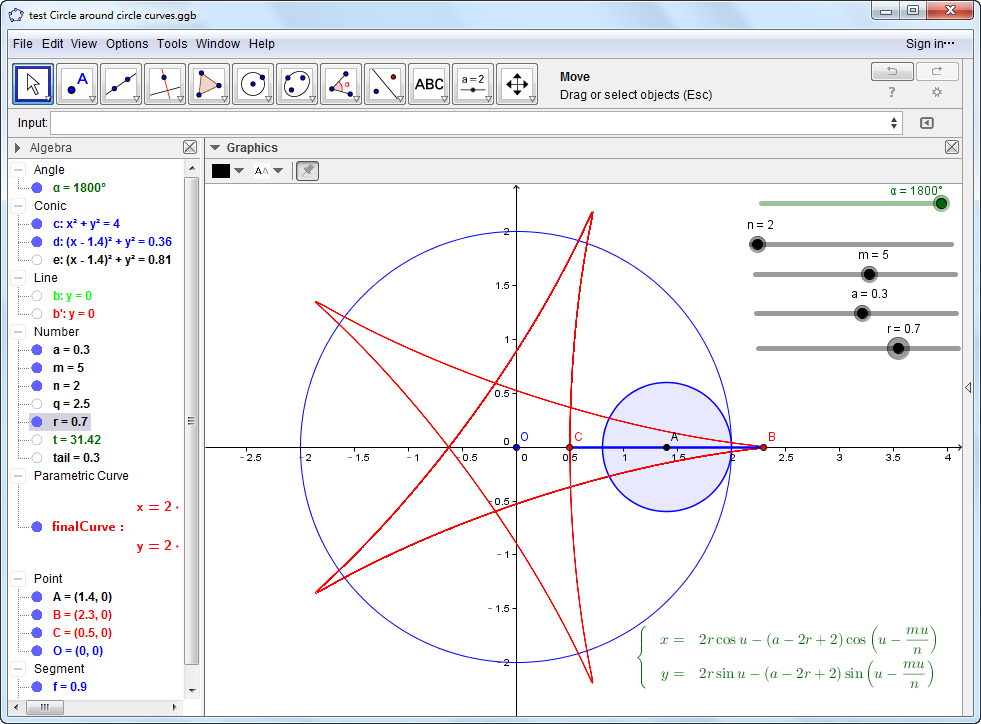
调整slider,可以观察每个参数对曲线的影响,原来正六边形是要这样....

再回想一下五角星时候的参数设置:

实际上最终的结果在五角星的情况下还作了反射,只是为了让动态GIF绘制曲线的时候,显示曲线的笔顺跟我手画类似曲线时的笔顺保持一致,alpha也是从-72°开始的.

参数方程中的参数可以任意取, 同一条曲线的参数方程因而并不唯一.

不忘初心, 让它俩都动起来(如果参数有所不同也不要奇怪,因为都可以)

最后我要问点开这篇博客看的同学一个问题,提一个忠告:

   (1) 同学你听说过安利吗?

   (2) Geogebra真是个好东西(免费开源). 还有Mathematica(个人版和教育版都便宜有折扣), 它们都是"初等数学和初级高等数学"学习的好伴侣.