Games101计算机图形学入门基础之一：向量变换、矩阵变换、视图变换、欧拉角与四元数

Games101计算机图形学入门基础之一：向量变换、矩阵变换、齐次坐标、欧拉角与四元数

前言

向量

Vectors（向量）：

在数学中，向量 （也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。
向量的记法： 印刷体记作黑体（粗体）的字母（如a、b、u、v），书写时在字母顶上加一小箭头“→”。 [1] 如果给定向量的起点（A）和终点（B），可将向量记作AB（并于顶上加→）。在空间直角坐标系中，也能把向量以数对形式表示，例如xOy平面中(2,3)是一向量。

向量加减与归一化

向量的加减：
遵循平行四边形法则，减法就看做成加上一个反方向的向量，如下图所示：

向量的归一化：

向量点乘叉乘及其作用

点乘：

点乘的作用：
由于点乘得到的是一个数字。两个向量越接近相乘的结果越接近于1，相乘大于0表明在同一方向，相乘小于0表明不在同一方向。

叉乘：

叉乘的应用:


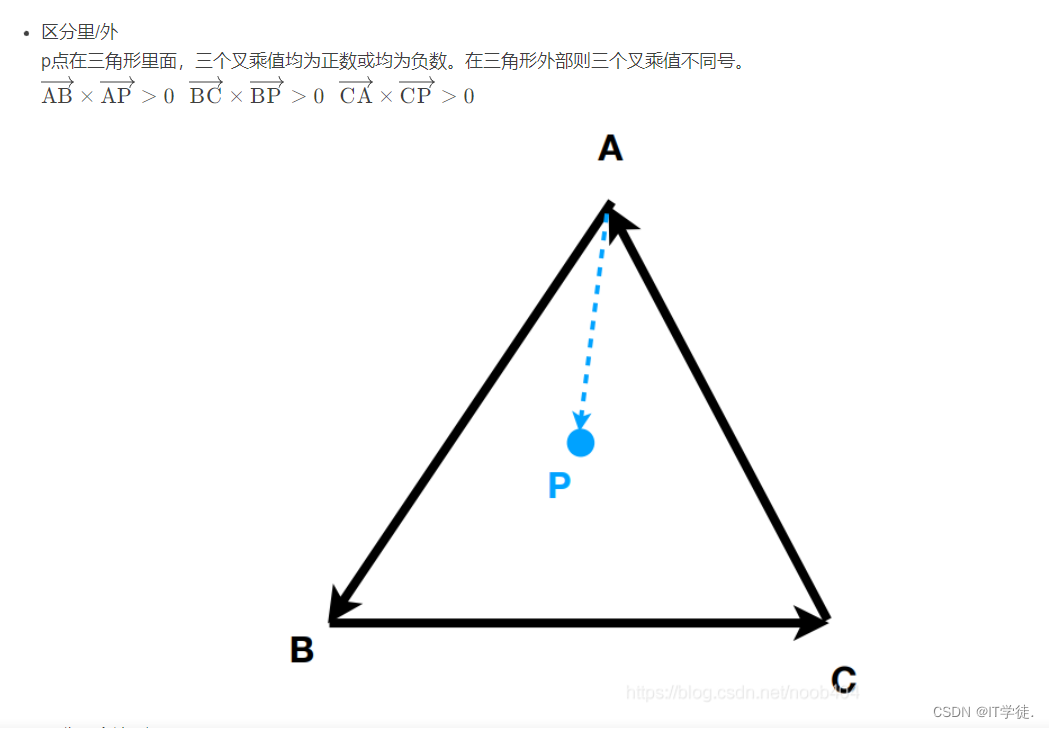
这里要着重记住点乘和叉乘的应用后面会不断用到。

矩阵

矩阵运算规则

在图形学中在图形学中被广泛应用于表达各种转换(Transformations),
$$\overrightarrow{Amn}\overrightarrow{ABmn}=Cmp$$其中矩阵A的列数必须等于矩阵B的行数，相乘结果的矩阵C行数和列数各为A的行数和。如下所示：

向量的叉乘可以写成矩阵作用形式：

矩阵转置和矩阵的逆

矩阵转置:

何为转置矩阵？将原矩阵A的行与列交换得到的新矩阵就是转置矩阵，用$A^T$表示。

矩阵的逆：

逆矩阵就是一个矩阵的逆向。比如一个点乘以一个矩阵后得到了一个新的点的位置，如果想通过这个点再获得矩阵转换前的位置，那我们就需要乘以这个矩阵的逆矩阵。

变换

变换矩阵 (Transformation Marices) 在图形学中的重要性不用多说，一切物体的缩放，旋转，位移，都可以通过变换矩阵作用得到。同时在投影 (projection) 变换的时候也有很多应用。

2D变换与3D变换

2D线性变换: 我们将如下图所示的简单矩阵乘法定义为对向量$(x,y{)}^T$的线性变换。

1. 缩放(scaling):
   缩放变换是一种沿着坐标轴作用的变换，定义如下:
   
   即除了$(0,0{)}^T$保持不变之外，所有的点变为$（S_{x}X,S_{y}Y{）}^T$
   举个例子：
   

2. 剪切(shearing)：
   shear变换直观理解就是把物体一边固定，然后拉另外一边，定义如下:
   
   分别对应着向"拉伸"x轴，和"拉伸"y轴。
   如下图所示：
   

3. 旋转(rotation)：
   旋转可以说是又一个十分重要的变换矩阵了，如下图，我们希望用一个变换矩阵表示将向量$\vec{a}$旋转到向量$\vec{b}|$的位置。
   
   
   3D线性变换:
   缩放不用多说:
   
   剪切也十分类似：
   
   3维旋转有3个矩阵，分别对应绕x轴，y轴，z轴旋转，同时有很关键的一点要注意！我们所采用的是右手系，因此旋转是有定向(orientation)正如在二维，是x轴向y轴旋转，对应到3维便是绕z轴旋转(x轴转向y轴)，不难推出绕x轴旋转(y转向z)，绕y轴旋转(z转向x), 如果想不明白，右手螺旋定则试一试就知道了！ x->y->z->x…因此理解了上面这个来看绕x和z旋转的变换矩阵

其实到这里可以下一个结论，可以看到任意旋转都是正交矩阵!，因此他们的逆便是他们的转置，而一个旋转矩阵的逆所对应的几何解释便是，我反着转这么多，比如我逆时针转30°，转置便是顺时针30°

注：以上所有的旋转都是针对原点来说，那么如何对围绕任何一个轴(3维)旋转呢?

3维绕任意轴旋转：
我们只有绕x，y, z旋转的方法，怎么随便给一个轴让你绕着他旋转呢！很直观的，我们把该轴给先旋转到任意的x，y，z轴上，然后就可以应用基本的旋转矩阵，最后再逆旋转回来即可，表示如下：
$R1RxR{1}^T\ast (x,y,z{)}^T$ 这里的Rx是知道的，问题只剩怎么求R1了，设我们想围绕旋转的轴为u uu，R1便是将u旋转到x的矩阵。具体来说这里我们需要以u为一轴，构造一个3维正交坐标系，然后将u-x对齐，那么其它两轴就肯定和y和z对齐了！构造如下，任取一t方向不与u重合

w = t x u
v = u x w

此时u, w, v便是我们构造出的新坐标系(这里运用了一些叉乘的小知识，读者不理解可取自行去了解一下叉乘几何含义再来看此式)。

好了，现在得到了u,w,v 对应 x,y,z如何将我们的新坐标系与原始坐标系重合呢，哈哈，这其实再简单不过了，我们取R1 = (u,w,v), 该旋转矩阵的含义便是将x , y , z x,y,zx,y,z旋转到u，w，v的旋转矩阵(不信可以直接R1 * x，R1y，R1z试试便一目了然)，还记得什么？我们上一节曾总结到，旋转矩阵是正交矩阵，旋转矩阵的转置便是它的逆，也是几何意义上的反作用，因此！$R^T$便是将u,w,v旋转到x,y,z的矩阵了。现在我们知道了R1知道了RX，那么围绕位移轴的旋转也就得到了！

中间那个矩阵换成 r o t a t e − x ( ϕ ) rotate-x(\phi)rotate−x(ϕ)就好啦.

仿射变换

齐次坐标

在上面的变换中我们知道了缩放,旋转,剪切三种线性的变换方式,但是有一种变换方式比较特殊,就是平移,如图所示:

我们发现这时候用一个矩阵乘以一个向量这种线性方式已经不能实现平移这种操作了,于是我们引入了齐次坐标的概念.我们可以利用齐次坐标来实现平移的相关操作(具体操作就是再引入一个"维度"t).
齐次坐标中：

对点进行位移操作：

我们之前所提到的线性变换如下：

发现不可能将二者合在一起用一个矩阵表示的，所以很自然的，我们引入一维新的坐标，称之为齐次坐标，(x,y)->(x,y,1)
具体操作如下:

现在我们就可以用一个矩阵即表示线性变换(先做)，又表示位移了(后做)！三维也是同理.

视图变换

坐标系转化

右手坐标系：伸开右手，大拇指指向X轴正方向，食指指向Y轴正方向，其他三个手指指向Z轴正方向
左手坐标系：伸开左手，大拇指指向X轴正方向，食指指向Y轴正方向，其他三个手指指向Z轴正方向
两者的区别主要是两者Z轴的方向是相反的

在OpenGL中使用的是右手坐标系,Unity使用左手坐标系，WebGL使用右手坐标系
此外Unity中还有四种坐标系:

• 世界坐标系: 当你从Unity中新建了一个物体对象，它所具有的Transform参数所采用的就是世界坐标系，该坐标系分为左手坐标系和右手坐标系，其中如图所示。其中左手坐标系就是Unity中的世界坐标系
• 屏幕坐标系: 就是把屏幕看作一个坐标系，从左下角开始计算，也就是(0,0)，而右上角则是(Screen.widht,Screen.height)，所以又叫做像素坐标系
• 视口坐标系: 该坐标系计算方式和屏幕坐标系类似，只不过把其参数标准化了，更加适用于比例计算。左下角为(0,0) 右上角为(1,1)
• GUI坐标系: 该坐标是从左上角开始计算的，左上角(0,0)，右下角为(Screen.width,Screen.height);
  想了解关于Unity内坐标的相关知识,可以参考此文: l详解Unity中的各种坐标系

“MVP变换”+视口变换

在这里插入图片描述

我们可以这样来描述视图变换的任务：将虚拟世界中以（x,y,z)为坐标的物体变换到 以一个个像素位置(x,y) 来表示的屏幕坐标系之中(2维)，这确实是一个较为复杂的过程，但是整个过程可以被细分为如下几个步骤：

(1) 模型变换(modeling tranformation)： 这一步的目的是将虚拟世界中或者更具体点，游戏场景中的物体调整至他们应该在的位置

(2) 摄像机变换(camera tranformation)： 在游戏中我们真正在乎的是摄像机(或者说眼睛)所看到的东西，也就是需要得到物体与摄像机的相对位置

(3) 投影变换(projection tranformation)： 根据摄像机变换得到了所有可视范围内的物体对于摄像机的相对位置坐标(x,y,z)之后，便是根据是平行投影还是透视投影，将三维空间投影至标准二维平面([-1,1]^2)之上 （tips：这里的z并没有丢掉，为了之后的遮挡关系检测）

(4) 视口变换(viewport transformation)： 将处于标准平面映射到屏幕分辨率范围之内，即[-1,1]^2→ \rightarrow→[0,width]*[0,height], 其中width和height指屏幕分辨率大小

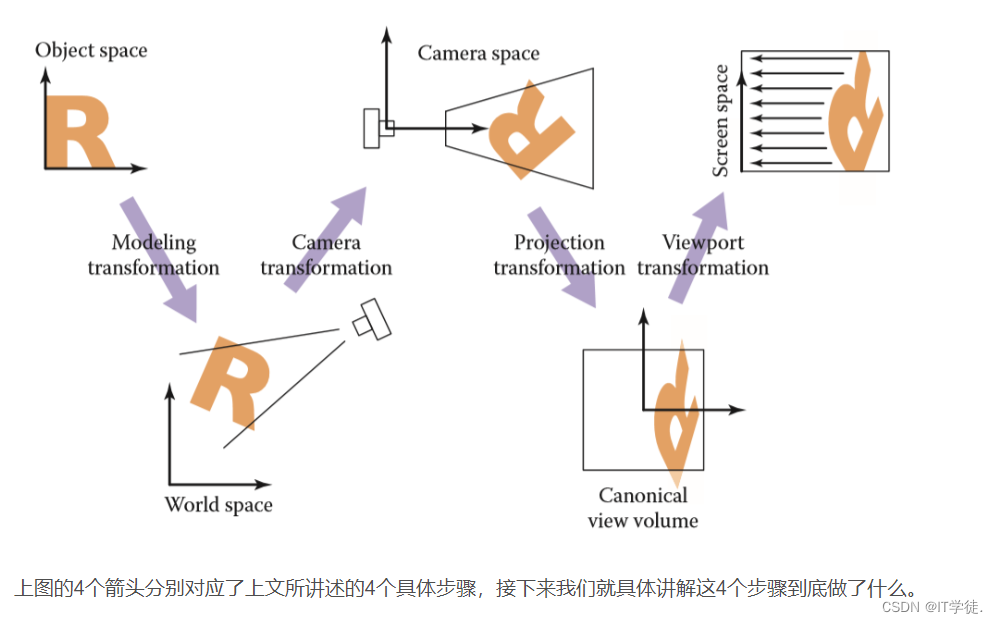
这里可以类比于我们拍一张苹果照片的这一场景
模型变换: 相当于"把苹果摆好",这里可以用上面所说的变换来实现将苹果摆放到合适的位置.
摄像机变换: 相当于"把相机摆好",摄像机变换的目的是得到所有可视物体与摄像机的相对位置，怎么得到？非常直观的一步，我们把物体和摄像机一起做移动，如果能够把摄像机的坐标轴(假设为u,v,w 分别对应原世界空间中的x,y,z)移动到标准的x，y，z轴，那么此时物体的坐标不自然便是相对坐标了吗！
因此核心问题就变成了如何表示或者说如何将camera的坐标系与原世界坐标系重合呢？我们先定义3个东西
相机或眼睛位置 (eye postion) e
观察方向 (gaze postion) g
视点正上方向 (view-up vector ) t
有了这三者定义之后，我们便可以建立摄像机坐标系了，定义如下：


(tips:这里为什么不直接拿 t 当做基底向量是因为摄像机的头可能是歪着看的，就像图中一样 )
如此成功建立摄像机坐标系之后，如何将其移动到原世界坐标系呢？
1 将相机位置移动至原点
2 通过旋转矩阵将二者坐标系重合
第一步只需简单的减去相机位置坐标 e 即可，而第二步通过矩阵变换也可以得到,只需用$(u,v,w{)}^T$矩阵便可轻松表示将摄像机坐标系旋转至世界坐标系了.

投影变换时除了摄像机之外另外一个重点，在经过摄像机变换之后得到的依然时三维空间中的顶点坐标，如何将其映射至二维空间坐标就交给投影变换完成。正如我们所熟知的那样投影又主要分为正交投影和透视投影，依次介绍

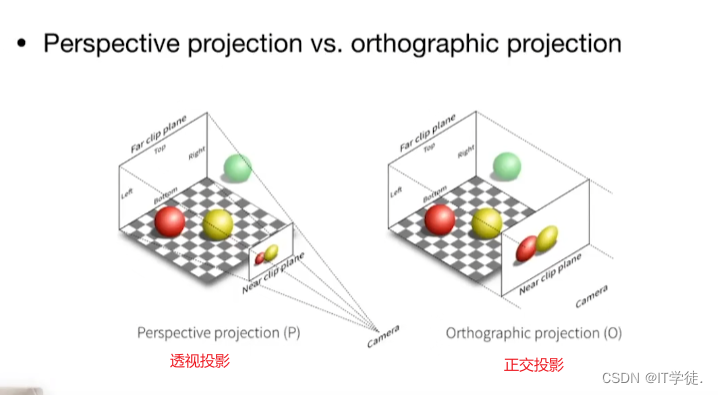
正交投影:
正交投影是相对简单的一种，坐标的相对位置都不会改变，所有光线都是平行传播，我们只需将物体（可视部分，即上图的那个长方体）全部转换到一个$[-1,1{]}^3$ 的空间之中即可（其中x，y坐标便是投影结果，保留z是为了之后的遮挡检测）,这里压缩到一个单位的空间向量里,也是为了计算方便.
透视投影:
透视投影就是最类似人眼所看东西的方式，遵循近大远小，
视口变换:
“窗口视口变换的目的是提供一种变换方式,让逻辑坐标能够在设备坐标中进行显示。用户输入的坐标一定是逻辑坐标,最终用来绘制的一定是经过窗口-视口变换后的视口坐标,也就是设备坐标(物理坐标)。”

欧拉角与四元数

前言

方位、方向、角位移

• 方位： 描述的是物体的朝向。要确定一个方位（orientation），却至少需要需要三个参数。
• 方向： “方向”和“方位”并不完全一样。向量有“方向”但没有“方位”，因为让向量自转，但向量却不会有任何变化。只要用两个数字（例如：极坐标），就能用参数表示一个方向（direction）。
• 角位移： 我们描述物体位置时并不是绝对坐标，而是描述相对于给定参考点的位移。同样，描述物体方位时，也不能使用绝对量。方位是通过与相对已知方位（通常称为"单位"方位或"源"方位）的旋转来描述的。旋转的量称作角位移。在数学上描述方位就等价于描述角位移。

欧拉角

欧拉角是描述方位的一种方法
什么是欧拉角：
欧拉角将方位（角位移）分解为绕三个互相垂直轴的旋转。任意三个轴和任意顺序都可以，但最有意义的是使用笛卡尔坐标系并按一定顺序所组成的旋转序列。
最常用的约定是所谓的“heading-pitch-bank”约定。它的基本思想是让物体开始于“标准”方位–就是物体坐标轴和惯性坐标轴对齐。
在标准方位上，让物体作heading、pitch、bank旋转，最后物体到达我们想要描述的方位。
首先，heading为绕y轴的旋转量，向右旋转为正：

heading
经过heading旋转，pitch为绕x轴的旋转量，注意是物体坐标系的x轴，不是原惯性坐标系的x轴：

pitch
经过了heading和pitch，bank为绕z轴的旋转量，注意是物体坐标系的z轴

bank
roll-pitch-yaw
heading-pitch-bank也叫做roll-pitch-yaw，roll等价于bank，yaw基本上等价于heading。注意，它的顺序和heading-pitch-bank的顺序相反，这只是语义上的。

roll-pitch-yaw

注意：
1、旋转可以以不同的顺序进行。
2、决定每个旋转的正方向时不一定必须遵守左手或右手法则。
欧拉角的优点：
欧拉角仅使用三个数来表达方位，并且这三个数都是角度。这使欧拉角具有一些独特的优点：
1、欧拉角对我们来说很容易使用。
2、最简洁的表达方式。
3、任意三个数都是合法的。
欧拉角的缺点：
给定方位的表达方式不唯一。
在将一个角度加上360度的倍数时，并不会改变方位。
还有一种情况，由三个角度不互相独立而导致的。例如，pitch135度等价于heading180度，pitch45度，然后bank180度。为了保证任意方位都只有独一无二的表示，必须限制角度的范围。一种常用的技术是将heading和bank限制在+180度到-180度之间，pitch限制在+90度到-90度之间。
万向锁：
欧拉角最著名的别名问题是这样的：先heading45度再pitch90度，这与先pitch90度再bank45度是等价的。事实上，一旦选择+(-)90度为pitch角，就被限制在只能绕竖直轴旋转。这种现象，角度为+(-)90度的第二次旋转使得第一次和第三次旋转的旋转轴相同，称作万向锁。为了消除限制欧拉角的这种别名现象，规定万向锁情况下由heading完成绕竖直轴的全部旋转。换句话说，在限制欧拉角中，如果pitch为+(-)90度，则bank为0。
两个角度间求插值;非常困难。
如果没有使用限制欧拉角，方位A的heading为720度，方位B的heading为45度，heading值;只相差45度，但简单的插值;
会在错误的方向上绕将近两周。
设A的heading为-170度，B的heading为170度。这两个值;只相差20度，但插值;操作又一次发生了错误，旋转是沿“长弧”绕了340度而不是更短的20度。
解决这类问题的方法是将插值的"差"角度折到-180度到180度之间，以找到最短弧。

四元数

什么是四元数？

在计算机图形学中，四元数用于物体的旋转，是一种较为复杂，但是效率较高的旋转方式。在三种坐标变换：旋转，平移，缩放当中，旋转应该算是比较复杂的存在。平常我们接触的比较多的是矩阵变换和欧拉变换。 对于一个物体的旋转，其实我们只需要知道四个值：一个旋转的向量 + 一个旋转的角度。而四元数也正是这样的设计：

其中x,y,z 代表的是向量的三维坐标，w代表的是角度；同时我们也可以写成以下的形式方便我们计算和分析：

q=(x,y,z,w)

其实，四元数本质上是一个超复数，

q=xi+yj+zk+w , $i^2$=$j^2$ =$k^2$ =−1
$q=[\vec{v},w]$

四元数的优缺点
内部由四个数字（在Unity中称为x，y，z和w）组成，然而这些数字不表示角度或轴，并且通常不需要直接访问它们。除非你特别有兴趣深入了解四元数学，你只需要知道四元数表示三维空间中的旋转，你通常不需要知道或修改x，y和z属性。
优点：
存储空间小，计算效率高。
四元旋转不存在万向节锁问题。
缺点：
四元数的数字表示不直观。
单个四元数不能表示在任何方向上超过180度的旋转。