向量的几何解释笔记（点积叉积矩阵）

在说这些概念以前一定要知道一件事情 ： 所有的数学定义都是由物理意义抽象而来，活着是为了某种计算方便而认为的定义的一种数学符号和数学运算规则：

1、行列式（获取两个向量张成的面积）

假设我有连个向量a b；我想求解这两个向量的张成的平行四边形的面积s

假设a = （ax ay）； 

       b = （bx by）；

       两向量之间的夹角为P ； 

       a与坐标轴的夹角为Pa；

       b与坐标轴的夹角为Pb

那么S = |a| * |b| * sin（P）；

其中sin（P） = sin（Pa - Pb） 

                      = sin（Pa）*cos（Pb） - cos（Pa）*sin（Pb）

                      = (bx / b)*(ax / a) - (by/b) * (ay/a);

所以 S = |a| * |b| * sin（P）

            = |a| * |b| * (bx / b)*(ax / a) - (by/b) * (ay/a) 

            = bx * ay - by*ax;

此时再来看看二阶行列式的定义 ：

|ax   ay |      

        |           |  = ax*by - ay*bx;

|bx   by |

看吧，认为的定义一个符号来简化计算而已

即det（a ， b） = s；

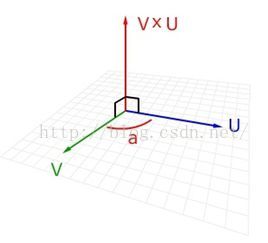
2、叉积（构建第三个向量，此向量与原来的两个向量垂直并且大小等于原来向量构建的平行四边形面积）

                                           

假设我有两个向量u ， v，此时我想构造第三个向量c，这个向量有两个特性：

第一 ： 此向量要垂直u v向量张成的平行四边形

第二 ： 此向量的长度等于u v向量张成的品行四边行的面积

假设 u = （ux uyuz）；

v = （vxvyvz）； 

c = （cx cycz）；

为了满足第一个特性；

那么c . b = 0 （a b向量的点积为0）；

c . a = 0 （c a向量的点积为0）；

那么得到 ：ux*cx  + uy*cy + uz * cz = 0；（1）

vx*cx  + vy*cy + vz * cz = 0； （2）

为了满足第三个特性c向量的长度等于  a b向量张成的品行四边行的面积；

此时需要注意一个地方，c是垂直ab张成的面积，所以c的长度如果以ab作为参考的话，就是cz的长度；

即|cz| = |u|*|v|*sin(a) ; (a为u v向量之间的夹角)；

即cz^2 = (vx*uy - vy*ux) ^2（3）

此处面积为vx*uy - vy*ux；是因为以此面积作为基准的话，

他其实是一个二维面，即vz 和 uz上不参与计算；

联立1 、 2 、 3求解方程组便可以求解得到满足向量c的cx cy cz

求解方程组可以得到c向量的解为 ：

cx　=　uy*vz - uz*vy;

cy = ux*vz - uz*vx;

cz = ux*vy - uy*vx;

因此得到向量c = （uy*vz - uz*vy ，ux*vz - uz*vx ，ux*vy - uy*vx）；

此时我们再来看叉积的定义 ：

u x v = （uy*vz - uz*vy ， ux*vz - uz*vx ， ux*vy - uy*vx）;

和上面的推导是一样，所以两个向量的叉积就是通过一定的变换得到了uv张成面的一个垂直向量，

且长度为uv向量张成平行四边形的面积。

3、点积（再求做功时力在作用方向上位移的乘积，理解为向量在另一个向量上的投影的乘积）

假设有两个向量A(X1 , Y1 ) ; B(X2 , Y2);

那么A向量在B向量上的投影为a*cos(pa); 其中a为A向量的长度pa为A向量的角度

那么A向量在B上的投影乘以B得到 ：ａ＊ｂ＊ｃｏｓ（ｐａ－ｐｂ）；

化简上面的表达式就可以得到：

ａ＊ｂ＊ｃｏｓ（ｐａ－ｐｂ）　＝　Ｘ１　＊　Ｘ２　＋　Ｙ１＊Ｙ２；

然而点积的定义：

ａ．ｂ　＝　Ｘ１　＊　Ｘ２　＋　Ｙ１＊Ｙ２；

4、向量空间基和秩的理解

在解析几何中，为了研究几何图形的变换，我们总是在一个固定的坐标系中讨论，进而把几何问题转化为代数问题。同样，在n

n维空间几何中，我们选定一组基底（n维）来应用向量和矩阵分析工具

假设一个空间中国有a1 a2 a3 。。。an是相互独立的

且该空间中的任意向量都可以由a1 a2 ... an任意线性表示。

那么称a1 a2 a3.。。an为该空间的一组基向量。

基向量前的参数表示了一个向量在这个基上的坐标。

而秩的值就等于基的个数，变相的表征了该空间的维度

基的选取不一定是垂直的，比如说对于二维空间来说，我可以任意选择两个向量来构建一个二维平面空间，并且这两个

向量可以不垂直。当然为了方便计算，我们需要来做坐标变换以使得这两个基转变为正交的，那样方便计算。所以对于

向量空间中的基不要尝试着想笛卡尔坐标系一样来做垂直线。

基向量组的选取是要注意顺序的，因为基的选取不同会导致和解析式上坐标顺序的改变，虽然数值不会改变

同样是对于三维系而言，三个不共面的向量可以组成一个三维的仿射坐标系（三个向量非互相垂直）。