7.6 高阶线性微分方程

 

 

第六节 高阶线性微分方程

在本节及以下两节，我们将讨论在实际问题中应用得较多的高阶线性微分方程，尤其是二阶线性微分方程。

一、二阶线性微分方程举例

例1：有阻尼的物体自由振动

设一个弹簧固定在上端，下端挂一个质量为 m 的物体。当物体静止时，重力与弹性力大小相等、方向相反，物体处于平衡位置。设 x 轴垂直向下，平衡位置为坐标原点。如果赋予物体初始速度 v_0 ≠ 0，物体将在平衡位置附近上下振动，其位置随时间 t 变化，可表示为 x(t)。为了确定振动规律，我们需要找到 x(t)。

根据力学，弹簧的弹性恢复力 f 与物体离开平衡位置的位移 x 成正比：

其中 c 是弹簧的劲度系数，负号表示弹性力与位移方向相反。

另外，物体在运动过程中会受到阻尼介质（如空气、油等）的阻力，使振动逐渐停止。实验表明，阻力 R 与物体的速度成正比：

其中 \mu 是阻力系数，负号表示阻力与运动方向相反。

根据牛顿第二定律，物体的加速度 a 满足：

将式子移项整理，并引入

我们得到二阶线性微分方程：

这是有阻尼条件下的物体自由振动方程。

如果物体还受到一个外部干扰力：

𝐹=𝐻sin⁡(𝑝𝑡),F=Hsin(pt),

则方程变为：

这是强迫振动的微分方程。

例2：串联电路振荡方程

设一个由电阻 R、自感 L 和电容 C 串联组成的电路，电源 E = E_0 \sin \omega t。设电流 i(t) 和电容器上的电荷 q(t) 满足：

根据回路电压定律：

可以得到：

这就是串联电路的振荡方程。

若撤去外电源（即 E = 0），方程简化为：

总结

虽然例1和例2涉及不同的实际问题，但它们的微分方程：

可以归纳为相同的形式。当 f(x) = 0 时，是齐次的线性微分方程，否则为非齐次的。

我们将在接下来的讨论中研究这些方程的解及其性质。

 

二、线性微分方程的解的结构

我们首先讨论二阶齐次线性方程：

定理1

如果函数 𝑦1(𝑥)y1​(x) 和 𝑦2(𝑥)y2​(x) 是方程（6-6）的两个解，那么：

也是方程（6-6）的解，其中 𝐶1C1​ 和 𝐶2C2​ 为任意常数。

证明：将方程（6-7）代入方程（6-6）的左端：

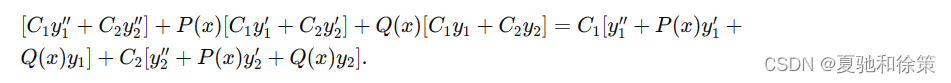
因为 𝑦1y1​ 和 𝑦2y2​ 都是方程（6-6）的解，所以右侧括号内的两个表达式恒等于零，方程的整体也等于零。因此，方程（6-7）是方程（6-6）的解。

注意：解（6-7）形式上包含两个任意常数 𝐶1C1​ 和 𝐶2C2​，但它不一定是方程（6-6）的通解。例如，如果 𝑦2(𝑥)=2𝑦1(𝑥)y2​(x)=2y1​(x)，那么方程（6-7）变为：

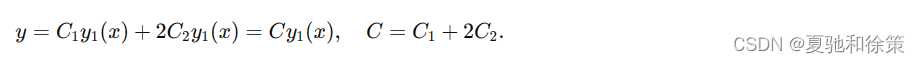
这显然不是方程（6-6）的通解。要确定方程（6-7）在何种情况下是通解，需要引入线性相关与线性无关的概念。

线性相关与线性无关

设 𝑦1(𝑥),𝑦2(𝑥),…,𝑦𝑛(𝑥)y1​(x),y2​(x),…,yn​(x) 是定义在区间 𝐼I 上的 𝑛n 个函数。如果存在 𝑛n 个不全为零的常数 𝑘1,𝑘2,…,𝑘𝑛k1​,k2​,…,kn​，使得在 𝑥∈𝐼x∈I 时有恒等式：

那么称这 𝑛n 个函数在区间 𝐼I 上线性相关，否则称为线性无关。

定理2

如果 𝑦1(𝑥)y1​(x) 和 𝑦2(𝑥)y2​(x) 是方程（6-6）的两个线性无关的特解，那么：

𝑦=𝐶1𝑦1(𝑥)+𝐶2𝑦2(𝑥),𝐶1,𝐶2为任意常数y=C1​y1​(x)+C2​y2​(x),C1​,C2​为任意常数

是方程（6-6）的通解。

例子：方程 𝑦′′+𝑦=0y′′+y=0 是二阶齐次线性方程，其中 𝑃(𝑥)=0P(x)=0，𝑄(𝑥)=1Q(x)=1。其解为：

𝑦1=cos⁡𝑥,𝑦2=sin⁡𝑥,y1​=cosx,y2​=sinx,

并且它们线性无关。因此，方程 𝑦′′+𝑦=0y′′+y=0 的通解为：

𝑦=𝐶1cos⁡𝑥+𝐶2sin⁡𝑥.y=C1​cosx+C2​sinx.

推论

如果 𝑦1(𝑥),𝑦2(𝑥),…,𝑦𝑛(𝑥)y1​(x),y2​(x),…,yn​(x) 是 𝑛n 阶齐次线性方程：

𝑦(𝑛)+𝑎1(𝑥)𝑦(𝑛−1)+…+𝑎𝑛−1(𝑥)𝑦′+𝑎𝑛(𝑥)𝑦=0y(n)+a1​(x)y(n−1)+…+an−1​(x)y′+an​(x)y=0

的 𝑛n 个线性无关的解，那么通解为：

𝑦=𝐶1𝑦1(𝑥)+𝐶2𝑦2(𝑥)+…+𝐶𝑛𝑦𝑛(𝑥),𝐶1,𝐶2,…,𝐶𝑛为任意常数。y=C1​y1​(x)+C2​y2​(x)+…+Cn​yn​(x),C1​,C2​,…,Cn​为任意常数。

定理3

设 𝑦∗(𝑥)y∗(x) 是二阶非齐次线性方程：

𝑦′′+𝑃(𝑥)𝑦′+𝑄(𝑥)𝑦=𝑓(𝑥)（方程6-5）y′′+P(x)y′+Q(x)y=f(x)（方程6-5）

的一个特解，𝑌(𝑥)Y(x) 是对应的齐次方程（6-6）的通解，则：

𝑦=𝑌(𝑥)+𝑦∗(𝑥)（方程6-8）y=Y(x)+y∗(x)（方程6-8）

是二阶非齐次线性微分方程（6-5）的通解。

证明：将方程（6-8）代入方程（6-5）的左端：

(Y'' + y^*'') + P(x) (Y' + y^*') + Q(x) (Y + y^*) = [Y'' + P(x) Y' + Q(x) Y] + [y^*'' + P(x) y^*' + Q(x) y^*].

因为 𝑌Y 是方程（6-6）的解，而 𝑦∗y∗ 是方程（6-5）的解，所以左侧两个括号内的表达式分别等于零和 𝑓(𝑥)f(x)，从而方程（6-8）两端相等，证明了它是方程（6-5）的解。

定理4

设非齐次线性方程（6-5）的右端 𝑓(𝑥)f(x) 是两个函数之和，即：

而 𝑦1(𝑥)y1​(x) 和 𝑦2(𝑥)y2​(x) 分别是方程：

𝑦′′+𝑃(𝑥)𝑦′+𝑄(𝑥)𝑦=𝑓1(𝑥),y′′+P(x)y′+Q(x)y=f1​(x),

与：

𝑦′′+𝑃(𝑥)𝑦′+𝑄(𝑥)𝑦=𝑓2(𝑥)y′′+P(x)y′+Q(x)y=f2​(x)

的特解，则：

𝑦=𝑦1(𝑥)+𝑦2(𝑥)y=y1​(x)+y2​(x)

是原方程的特解。

证明：将方程（6-9）的左端代入：

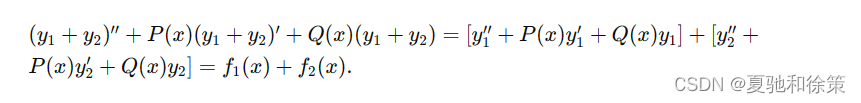
因此，𝑦1+𝑦2y1​+y2​ 是方程（6-9）的一个特解。

这一定理被称为线性微分方程的解的叠加原理。定理3和定理4也可以推广到 𝑛n 阶非齐次线性方程。

 

 

三、常数变易法

在第四节中，为了解一阶非齐次线性方程，我们使用了常数变易法。其特点是：如果 𝐶⋅𝑦1(𝑥)C⋅y1​(x) 是齐次线性方程的通解，那么可以利用变换 𝑦=𝑢⋅𝑦1(𝑥)y=u⋅y1​(x)（将齐次方程通解中的常数 𝐶C 替换为未知函数 𝑢(𝑥)u(x)）去解非齐次线性方程。这一方法也适用于解高阶线性方程。下面以二阶线性方程为例进行讨论。

如果已知齐次方程 (6-6) 的通解为：

那么可以用如下的常数变易法去求非齐次方程 (6-5) 的通解。令：

我们要确定未知函数 𝑣1(𝑥)v1​(x) 和 𝑣2(𝑥)v2​(x)，使 (6-10) 所表示的函数满足非齐次方程 (6-5)。为此，对 (6-10) 式求导，得：

由于两个未知函数 𝑣1v1​ 和 𝑣2v2​ 只需满足 (6-5) 一个关系式，因此我们还可以令它们满足另一个关系式：

𝑦1𝑣′+𝑦2𝑣′=0.y1​v′+y2​v′=0.

从而：

𝑦′=𝑦1′𝑣1+𝑦2′𝑣2.y′=y1′​v1​+y2′​v2​.

再求导，得：

𝑦′′=𝑦1′′𝑣1+𝑦2′′𝑣2+𝑦1′𝑣′+𝑦2′𝑣′.y′′=y1′′​v1​+y2′′​v2​+y1′​v′+y2′​v′.

将 𝑦y、𝑦′y′ 和 𝑦′′y′′ 代入方程 (6-5)，得：

(𝑦1′′𝑣1+𝑦2′′𝑣2+𝑦1′𝑣′+𝑦2′𝑣′)+𝑃(𝑦1′𝑣1+𝑦2′𝑣2)+𝑄(𝑦1𝑣1+𝑦2𝑣2)=𝑓.(y1′′​v1​+y2′′​v2​+y1′​v′+y2′​v′)+P(y1′​v1​+y2′​v2​)+Q(y1​v1​+y2​v2​)=f.

整理得：

𝑦1′𝑣′+𝑦2′𝑣′+(𝑦1′′+𝑃𝑦1′+𝑄𝑦1)𝑣1+(𝑦2′′+𝑃𝑦2′+𝑄𝑦2)𝑣2=𝑓.y1′​v′+y2′​v′+(y1′′​+Py1′​+Qy1​)v1​+(y2′′​+Py2′​+Qy2​)v2​=f.

注意到 𝑦1y1​ 和 𝑦2y2​ 是齐次方程 (6-6) 的解，因此上式即为：

𝑦1′𝑣′+𝑦2′𝑣′=𝑓.y1′​v′+y2′​v′=f.

联立方程 (6-11) 与 (6-12)，在系数行列式：

𝑊=∣𝑦1𝑦2𝑦1′𝑦2′∣≠0W=∣∣​y1​y1′​​y2​y2′​​∣∣​=0

时，可以解得：

𝑣1′=−𝑦2𝑓𝑊,𝑣2′=𝑦1𝑓𝑊.v1′​=W−y2​f​,v2′​=Wy1​f​.

对上两式积分（假定 𝑓(𝑥)f(x) 连续），得：

𝑣1=∫−𝑦2𝑓𝑊 𝑑𝑥,𝑣2=∫𝑦1𝑓𝑊 𝑑𝑥.v1​=∫W−y2​f​dx,v2​=∫Wy1​f​dx.

于是，非齐次方程 (6-5) 的通解为：

𝑦=𝐶1𝑦1+𝐶2𝑦2+𝑦1∫−𝑦2𝑓𝑊 𝑑𝑥+𝑦2∫𝑦1𝑓𝑊 𝑑𝑥.y=C1​y1​+C2​y2​+y1​∫W−y2​f​dx+y2​∫Wy1​f​dx.

例 3

已知齐次方程 (𝑥−1)𝑦′′−𝑥𝑦′+𝑦=0(x−1)y′′−xy′+y=0 的通解为：

𝑌(𝑥)=𝐶1𝑥+𝐶2𝑒𝑥,Y(x)=C1​x+C2​ex,

求非齐次方程 (𝑥−1)𝑦′′−𝑥𝑦′+𝑦=(𝑥−1)2(x−1)y′′−xy′+y=(x−1)2 的通解。

解：把所给方程写成标准形式：

𝑦′′−𝑥𝑥−1𝑦′+1𝑥−1𝑦=𝑥−1.y′′−x−1x​y′+x−11​y=x−1.

令：

按照 (6-11) 和 (6-12) 的关系，有：

解得：

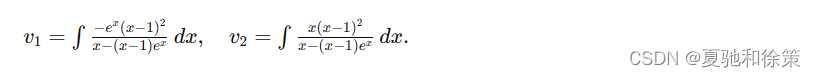
积分得：

于是所求非齐次方程的通解为：

 

 

三、常数变易法

在第四节中，为了解一阶非齐次线性方程，我们使用了常数变易法。其特点是：如果 𝐶⋅𝑦1(𝑥)C⋅y1​(x) 是齐次线性方程的通解，那么可以利用变换 𝑦=𝑢⋅𝑦1(𝑥)y=u⋅y1​(x)（将齐次方程通解中的常数 𝐶C 替换为未知函数 𝑢(𝑥)u(x)）去解非齐次线性方程。这一方法也适用于解高阶线性方程。下面以二阶线性方程为例进行讨论。

如果已知齐次方程 (6-6) 的通解为：

那么可以用如下的常数变易法去求非齐次方程 (6-5) 的通解。令：

𝑦=𝑦1(𝑥)𝑣1+𝑦2(𝑥)𝑣2,y=y1​(x)v1​+y2​(x)v2​,

(6-10)

我们要确定未知函数 𝑣1(𝑥)v1​(x) 和 𝑣2(𝑥)v2​(x)，使 (6-10) 所表示的函数满足非齐次方程 (6-5)。为此，对 (6-10) 式求导，得：

𝑦′=𝑦1𝑣′+𝑦2𝑣′+𝑦1′𝑣1+𝑦2′𝑣2.y′=y1​v′+y2​v′+y1′​v1​+y2′​v2​.

由于两个未知函数 𝑣1v1​ 和 𝑣2v2​ 只需满足 (6-5) 一个关系式，因此我们还可以令它们满足另一个关系式：

𝑦1𝑣′+𝑦2𝑣′=0.y1​v′+y2​v′=0.

从而：

𝑦′=𝑦1′𝑣1+𝑦2′𝑣2.y′=y1′​v1​+y2′​v2​.

再求导，得：

𝑦′′=𝑦1′′𝑣1+𝑦2′′𝑣2+𝑦1′𝑣′+𝑦2′𝑣′.y′′=y1′′​v1​+y2′′​v2​+y1′​v′+y2′​v′.

将 𝑦y、𝑦′y′ 和 𝑦′′y′′ 代入方程 (6-5)，得：

(𝑦1′′𝑣1+𝑦2′′𝑣2+𝑦1′𝑣′+𝑦2′𝑣′)+𝑃(𝑦1′𝑣1+𝑦2′𝑣2)+𝑄(𝑦1𝑣1+𝑦2𝑣2)=𝑓.(y1′′​v1​+y2′′​v2​+y1′​v′+y2′​v′)+P(y1′​v1​+y2′​v2​)+Q(y1​v1​+y2​v2​)=f.

整理得：

𝑦1′𝑣′+𝑦2′𝑣′+(𝑦1′′+𝑃𝑦1′+𝑄𝑦1)𝑣1+(𝑦2′′+𝑃𝑦2′+𝑄𝑦2)𝑣2=𝑓.y1′​v′+y2′​v′+(y1′′​+Py1′​+Qy1​)v1​+(y2′′​+Py2′​+Qy2​)v2​=f.

注意到 𝑦1y1​ 和 𝑦2y2​ 是齐次方程 (6-6) 的解，因此上式即为：

𝑦1′𝑣′+𝑦2′𝑣′=𝑓.y1′​v′+y2′​v′=f.

联立方程 (6-11) 与 (6-12)，在系数行列式：

𝑊=∣𝑦1𝑦2𝑦1′𝑦2′∣≠0W=∣∣​y1​y1′​​y2​y2′​​∣∣​=0

时，可以解得：

𝑣1′=−𝑦2𝑓𝑊,𝑣2′=𝑦1𝑓𝑊.v1′​=W−y2​f​,v2′​=Wy1​f​.

对上两式积分（假定 𝑓(𝑥)f(x) 连续），得：

𝑣1=∫−𝑦2𝑓𝑊 𝑑𝑥,𝑣2=∫𝑦1𝑓𝑊 𝑑𝑥.v1​=∫W−y2​f​dx,v2​=∫Wy1​f​dx.

于是，非齐次方程 (6-5) 的通解为：

𝑦=𝐶1𝑦1+𝐶2𝑦2+𝑦1∫−𝑦2𝑓𝑊 𝑑𝑥+𝑦2∫𝑦1𝑓𝑊 𝑑𝑥.y=C1​y1​+C2​y2​+y1​∫W−y2​f​dx+y2​∫Wy1​f​dx.

例 3

已知齐次方程 (𝑥−1)𝑦′′−𝑥𝑦′+𝑦=0(x−1)y′′−xy′+y=0 的通解为：

𝑌(𝑥)=𝐶1𝑥+𝐶2𝑒𝑥,Y(x)=C1​x+C2​ex,

求非齐次方程 (𝑥−1)𝑦′′−𝑥𝑦′+𝑦=(𝑥−1)2(x−1)y′′−xy′+y=(x−1)2 的通解。

解：把所给方程写成标准形式：

𝑦′′−𝑥𝑥−1𝑦′+1𝑥−1𝑦=𝑥−1.y′′−x−1x​y′+x−11​y=x−1.

令：

𝑦=𝑥𝑣1+𝑒𝑥𝑣2.y=xv1​+exv2​.

按照 (6-11) 和 (6-12) 的关系，有：

𝑣1′=−𝑒𝑥(𝑥−1)2𝑥−(𝑥−1)𝑒𝑥,𝑣2′=𝑥(𝑥−1)2𝑥−(𝑥−1)𝑒𝑥.v1′​=x−(x−1)ex−ex(x−1)2​,v2′​=x−(x−1)exx(x−1)2​.

解得：

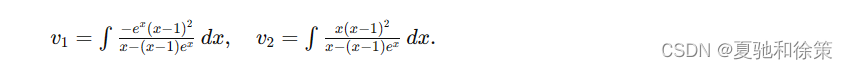
积分得：

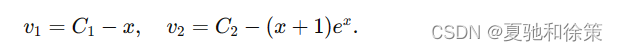
于是所求非齐次方程的通解为：