傅里叶变化的探索

对于离散信号，存在着两种傅里叶变换：

1. 离散时间傅里叶变换(DTFT)，用于求离散信号的连续频谱
2. 离散傅里叶变换(DFT)，用来求连续频谱上的离散样本点，相当于对连续频谱进行等间隔的采样，因此，时域和频域都是离散的。

傅里叶的意义

1. 傅里叶变换是将信号用不同的单频信号线性组合，其是线性滤波的核心概念。
2. 其是解决实际问题的工具，它被广泛地使用并作为基础工具学习。它可以使我们工作在“频率域”，而且在转换回信号的原始域时不丢失任何信息。
3. 一个恰当的比喻是是将傅里叶变换比做一个玻璃棱镜，棱镜是可将光分成不同颜色（由波长或频率决定）成分的物理仪器。
4. 频率域可以看成一个“实验室”，可利用信号外表和频率成分之间的对应关系，解决外表非常困难、复杂的任务。

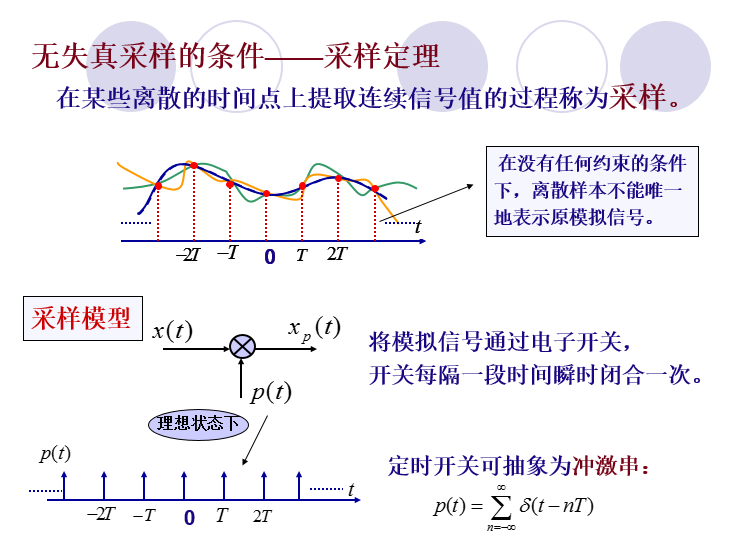
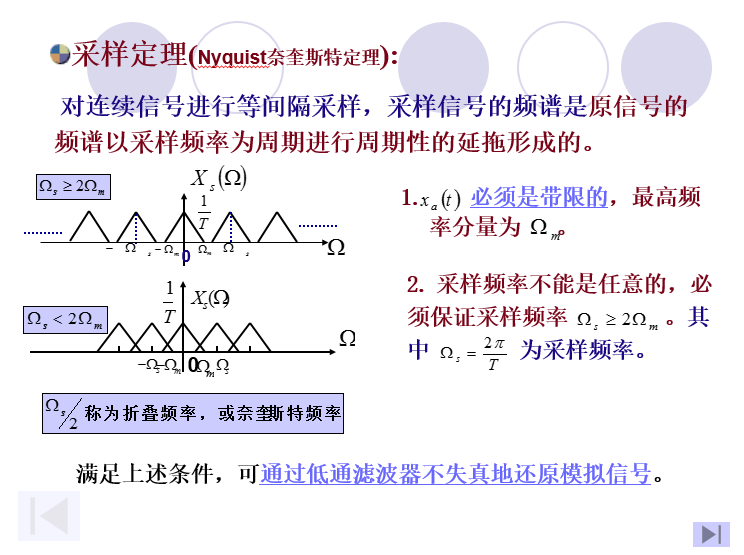
采样定理(Nyquist奈奎斯特定理):

对连续的信号进行采样，要用连续信号与单位冲击函数做运算。如图所示：

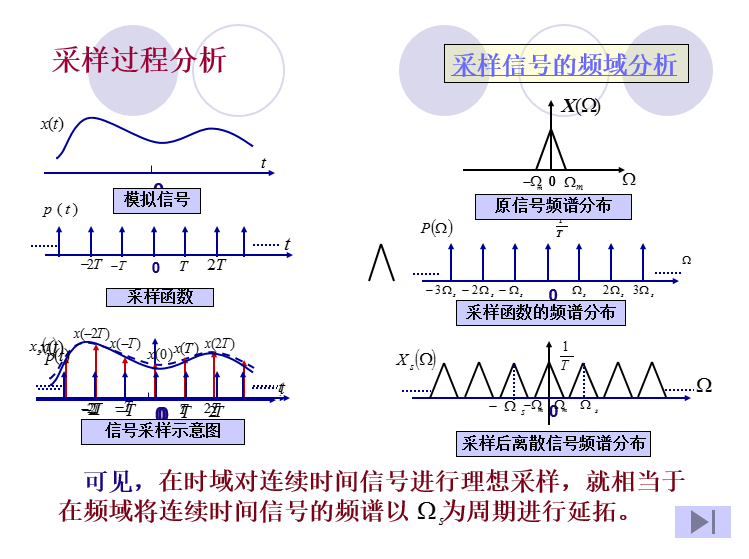
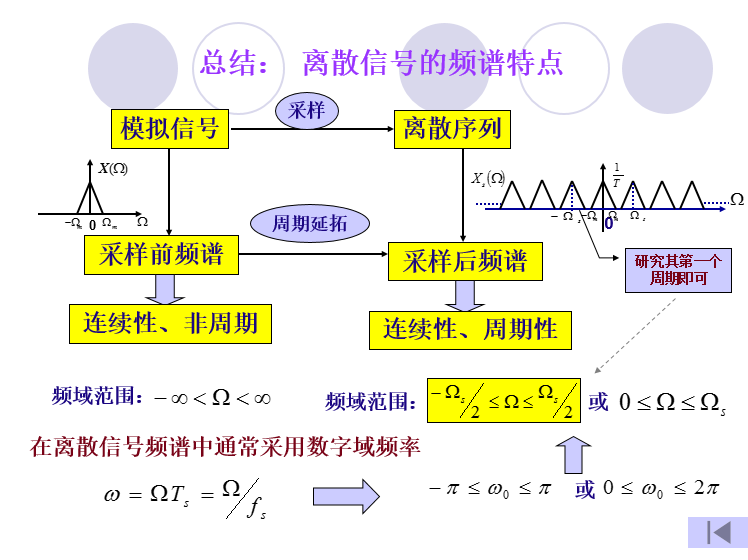
对连续信号进行等间隔采样，采样信号的频谱是原信号的频谱以采样频率为周期进行周期性的延拖形成的。

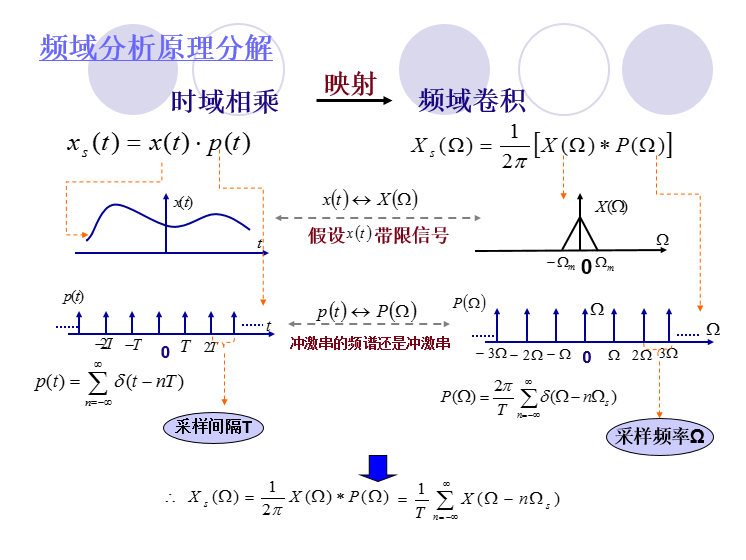
时间域的相乘等于频域的卷积：

采样的频率要大于2倍的频域最高频率分量。

离散信号的特点

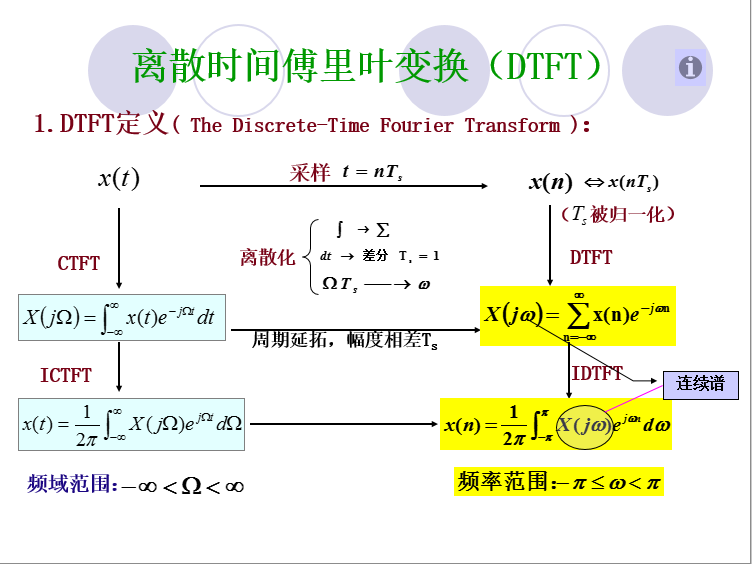
离散时间傅里叶变换（DTFT）

下面用matlab实现DTFT:
也可以使用matlab自带的函数