《高等数学》学习笔记一：函数与极限

自学的，随便看看就行（
以前写的高中数学选修2-2学习笔记，也可以看看，不过是一些比较基础的东西，对做题没太大帮助（

一、函数与极限

1.1 函数的极限

1.1.1 函数极限的定义

1.1.1.1 相关定义

邻域：$(x_0-\delta ,x_0+\delta )$称为以$x_0$为中心，半径为$\delta$的邻域。
去心邻域：$(x_0-\delta ,x_0)\cup (x_0,x_0+\delta )$称为去心邻域（相当于邻域挖掉了中心）
邻域也可表示为$0\le |x-x_0|<\delta$，去心邻域也可表示为$0<|x-x_0|<\delta$。

反三角函数是三角函数（在某个定义域上）的反函数。举例：
$y=\sin x$是三角函数，如果此时我们要用$y$表示$x$，可以表示为$x=\arcsin y$。
显然三角函数值域为$[-1,1]$，即$y\in [-1,1]$。但是一个三角函数值可以对应无数个角。
我们发现：$[-\frac{\pi }{2},\frac{\pi }{2}]$内任意两角$\sin$不同，$[0,\pi ]$内任意两角$\cos$不同，$[-\frac{\pi }{2},\frac{\pi }{2}]$内任意两角$\tan$不同。
因此规定在$[-\frac{\pi }{2},\frac{\pi }{2}]$内$\sin$值（或$\tan$值）分别等于$y$的$x$，记作$x=\arcsin y$（或$x=\arctan y$，$\arctan$的值域要挖去$\pm \frac{\pi }{2}$）。
在$[0,\pi ]$内$\cos$值为$y$的$x$，满足$x=\arccos y$。

一些奇怪的性质：
$1.\sin (\arcsin x)=\cos (\arccos x)=\tan (\arctan x)=x$（大概是很显然的

$2.\sin (\arccos x)=\cos (\arcsin x)=\sqrt{1-x^2}$
证明：令$t=\arccos x$，则$x=\cos t$，$t\in [0,\pi ]$。在此区间内$\sin t\ge 0$，因此$\sin t=\sqrt{1-{\cos }^{2}t}=\sqrt{1-x^2}$。
令$m=\arcsin x$，则$x=\sin m$，$m\in [-\frac{\pi }{2},\frac{\pi }{2}]$。在此区间内$\cos m\ge 0$，因此$\cos m=\sqrt{1-{\sin }^{2}m}=\sqrt{1-x^2}$。

$3.y=\arcsin x$，则$y^{\prime }=\frac{1}{1-x^2}$。（目前超纲*）
证明：由$y=\arcsin x$得$x=\sin y$。两边同时加上$\frac{d}{dx}$（即同时对$x$求导）得：
$\frac{dx}{dx}=\frac{d\sin y}{dx}$
左边化简得1，右边变形得：$1=\frac{d\sin y}{dy}\ast \frac{dy}{dx}$。
我们知道$\sin x$导数是$\cos x$，因此$\frac{d\sin y}{dy}=\cos y$。而$\frac{dy}{dx}$就是$y$对$x$的导数，即$y^{\prime }$。
所以$y^{\prime }=\frac{1}{\cos y}=\frac{1}{\cos (\arcsin x)}=\frac{1}{\sqrt{1-x^2}}$

$4.y=\arccos x$，则$y^{\prime }=-\frac{1}{\sqrt{1-x^2}}$（证明方法类似
$5.y=\arctan x$，则$y^{\prime }=\frac{1}{1+x^2}$

1.1.1.2 函数趋于某个实数的极限

极限有两种情况：一种是趋于某个实数的极限，另一种是趋于无穷的极限。
先考虑趋于某个实数的情况：
假设有一个函数$f(x)$，它在$x_0$的某去心邻域上有定义。
$f(x)$在$x_0$处极限为$A$的定义为：$\forall ϵ>0$，$\exists \delta >0$，使$(x_0-\delta ,x_0)\cup (x_0,x_0+\delta )$内，满足$|f(x)-A|<ϵ$。
此时记为：$$\underset{x\to x_0}{\lim }f(x)=A$$
看起来很恐怖，其实很简单：就是在$x_0$附近的点的函数值都不离$A$太远。
下面来证明几个显然的极限：
1.$f(x)=c$ ($c$为常数)。证明$\underset{x\to x_0}{\lim }f(x)=c$。
证明：对于$\forall ϵ>0$，任取$\delta >0$，在$(x_0-\delta ,x_0)\cup (x_0,x_0+\delta )$内，$|f(x)-c|=|c-c|=0<ϵ$。
因此$\underset{x\to x_0}{\lim }f(x)=c$。

2.$f(x)=114x+514$，证明$\underset{x\to 0}{\lim }f(x)=514$（好时代，来临罢！）
分析：这看起来很显然（代入0就是514），但如何取这个$\delta$？我们不妨倒推，如果要想让$|f(x)-514|<ϵ$，就要让$|114x|<ϵ$，即$|x|<\frac{ϵ}{114}$，也就是$|x-0|<\frac{ϵ}{114}$。
那么我们取$\delta =\frac{ϵ}{114}$就好。

证明：对于$\forall ϵ>0$，取$\delta =\frac{ϵ}{114}$，在$(-\delta ,0)\cup (0,\delta )$内，$|f(x)-514|=|114x|$。
由于$|x|<\delta =\frac{ϵ}{114}$，所以$|f(x)-514|=114|x|<ϵ$。
因此$\underset{x\to 0}{\lim }f(x)=514$。（Q.E.D）

判断：已知$f(x)$在$x_0$处有定义且极限存在，那么$\underset{x\to x_0}{\lim }f(x)=f(x_0)$
这是非常错误的（rxj化），因为$f(x)$可以在$x_0$处不连续 /jy
比如当$x<0$或$x>0$时，$f(x)=x$；当$x=0$时，$f(x)=1919810$。（无端恶臭）
那么$\underset{x\to 0}{\lim }f(x)=0$，但是$f(0)=1919810$，二者并不相等。

左极限：若$\forall ϵ>0$，$\exists \delta >0$，在$x\in (x_0-\delta ,x_0)$时，$|f(x)-A|<ϵ$，则把$A$称为$f(x)$在$x_0$处的左极限，记为$\underset{x\to x_0^{-}}{\lim }f(x)=A$。
右极限：若$\forall ϵ>0$，$\exists \delta >0$，在$x\in (x_0,x_0+\delta )$时，$|f(x)-A|<ϵ$，则把$A$称为$f(x)$在$x_0$处的右极限，记为$\underset{x\to x_0^{+}}{\lim }f(x)=A$。
可以看出，左极限和右极限与极限的定义基本相同，只是改了个定义域。
易知：函数极限存在的充要条件，就是左极限和右极限都存在，且左右极限相等（就是取个并集嘛

举例：$f(x)=|x|$，求导得$f^{\prime }(x)$，那么$\underset{x\to 0^{-}}{\lim }{f}^{\prime }(x)=-1$，$\underset{x\to 0^{+}}{\lim }{f}^{\prime }(x)=1$，左右极限不相等，所以$f^{\prime }(x)$在$x=0$处的极限不存在。

1.1.1.3 函数趋于无穷的极限

$f(x)$趋于无穷时极限为$A$的定义为：$\forall ϵ>0$，$\exists X>0$，使$|x|>X$时，有$|f(x)-A|<ϵ$。
其实也很简单：当$|x|$大到一定程度时，$f(x)$就不能离$|A|$太远。
注意这里的无穷可以是正无穷也可以是负无穷，因此$x$的范围要加绝对值。
同样来证明一些显然的东西：证明$\underset{x\to \infty }{\lim }\frac{1}{x}=0$。
证：对于$\forall ϵ>0$，取$X=\frac{1}{ϵ}$，则当$|x|>X=\frac{1}{ϵ}$时，$|f(x)-0|=|\frac{1}{x}|<ϵ$。
因此$\underset{x\to \infty }{\lim }\frac{1}{x}=0$。

1.1.2 函数极限的性质

1.函数在某个点上的极限唯一。（难道能既趋近114又趋近514吗（无慈悲

2.局部有界性：若$\underset{x\to x_0}{\lim }=A$，则$\exists M>0,\delta >0$，对于$0<|x-x_0|<\delta$，有$|f(x)|\le M$。（$M$就是“界”）
证明也简单：由$\underset{x\to x_0}{\lim }=A$可得$\forall ϵ>0$，$\exists \delta >0$，在$0<|x-x_0|<ϵ$时，有$|f(x)-A|<ϵ$。
那么我们任取一个$ϵ$，找到使后面那坨成立的$\delta$。由绝对值三角不等式，$|f(x)|=|f(x)-A+A|\le |f(x)-A|+|A|<ϵ+A$。
于是取$M=ϵ+A$即可使$0<|x-x_0|<\delta$时$|f(x)|\le M$。

3.局部保号性（zjm狂喜）：若$\underset{x\to x_0}{\lim }f(x)=A>0$，则$\exists \delta >0$，使$0<|x-x_0|<\delta$时，$f(x)>0$。（大于0就是“保号”，小于0同理）
证明：取$ϵ=A$（

注：高考导数大题用局部保号性要被扣分，但如果只剩三分钟了那你尽管用（

4.假设数列 { a n } \{a_n\} {an​}满足$\underset{n\to +\infty }{\lim }{a}_n=x_0$（数列极限见1.2），且$\underset{x\to x_0}{\lim }f(x)=A$，则$\underset{n\to +\infty }{\lim }f(a_n)=A$。
证明：由$\underset{x\to x_0}{\lim }f(x)=A$可知，任取$ϵ>0$，$\exists \delta >0$，对于$0<|x-x_0|<\delta$，满足$|f(x)-A|<ϵ$。
由$\underset{n\to +\infty }{\lim }{a}_n=x_0$可知，取${ϵ}^{\prime }=\delta$，$\exists n_0\in {\mathbb{Z}}^{+}$，使$n>n_0$时，$|a_n-x_0|<{ϵ}^{\prime }=\delta$。则此时$|f(a_n)-A|<ϵ$。
因此$\underset{n\to +\infty }{\lim }f(a_n)=A$。

5.夹逼定理：假设$g(x)\le f(x)\le h(x)$在$x_0$的某个去心邻域内成立，且$\underset{x\to x_0}{\lim }g(x)=\underset{x\to x_0}{\lim }h(x)=A$，则$\underset{x\to x_0}{\lim }f(x)=A$。
这个定理很好理解，$f(x)$在$g(x)$和$h(x)$之间，在$x_0$处极限都为$A$，两边夹（czf语），那$f(x)$在$x_0$处极限也为$A$。
证明：任取$ϵ>0$，$\exists {\delta }_1>0$，使$0<|x-x_0|<{\delta }_1$时，$|g(x)-A|<ϵ$；$\exists {\delta }_2>0$，使$0<|x-x_0|<{\delta }_2$时，$|h(x)-A|<ϵ$。
取$\delta =\min ({\delta }_1,{\delta }_2)$，则在半径为$\delta$的去心邻域内，$|g(x)-A|<ϵ$，$|h(x)-A|<ϵ$。
因此该范围内$g(x)>A-ϵ,h(x)<A+ϵ$。
又由$g(x)\le f(x)\le h(x)$得$A-ϵ<f(x)<A+ϵ$，即$|f(x)-A|<ϵ$。
因此$\forall ϵ>0,\exists \delta >0,$使$0<|x-x_0|<\delta$时，$|f(x)-A|<ϵ$。故$\underset{x\to x_0}{\lim }f(x)=A$。

由夹逼定理可以推导出一个重要极限：$$\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$$
证明过程看选修2-2学刁笔记（

1.1.3 函数极限的运算规则

补充一个重要极限：$$\underset{n\to +\infty }{\lim }(1+\frac{1}{n}{)}^n=e$$
也可以表示为$\underset{n\to 0}{\lim }(1+n{)}^{\frac{1}{n}}=e$，两者是等价的。

运算规则：
1.有界函数与无穷小量的乘积为无穷小。
这一条准则比较有用，例如：求$\underset{x\to 0}{\lim }x\sin \frac{1}{x}$。
$\frac{1}{x}$在0附近的变化速度很大，$\sin \frac{1}{x}$在$0$附近剧烈震荡，它在$x\to 0$时甚至不存在极限。（$\sin (+\infty )$是1？0？-1？）
但由于函数$y=\sin x$是有界函数，所以$y=\sin \frac{1}{x}$也是有界函数（$|y|\le 1$）
而$x$此时是无穷小量，因此$\underset{x\to 0}{\lim }x\sin \frac{1}{x}=0$。

再求一个：$\underset{x\to +\infty }{\lim }\frac{\sin (\tan 114x+514)}{x}=\underset{x\to +\infty }{\lim }\sin (...)\ast \frac{1}{x}=0$。

2.假设$\underset{x\to x_0}{\lim }f(x)=A,\underset{x\to x_0}{\lim }g(x)=B$。
则$\underset{x\to x_0}{\lim }f(x)\pm g(x)=A\pm B$，$\underset{x\to x_0}{\lim }f(x)g(x)=AB$，$\underset{x\to x_0}{\lim }\frac{f(x)}{g(x)}=\frac{A}{B}(B\ne 0)$。
注意：这一条成立的前提是$f(x)$和$g(x)$的极限均存在。（和$\ln AB=\ln A+\ln B$类似，要求$A,B$均为正数）
推论：$\underset{x\to x_0}{\lim }f(x{)}^n=[\underset{x\to x_0}{\lim }f(x){]}^n$
注：以上结论也适用于$x\to +\infty$的情况。
举例：求$\underset{x\to 1}{\lim }\frac{x^2+2x+1}{x+3}$
分析：我们发现分式上下都不为0，极限都存在，因此直接代入$x=1$就行。
$\underset{x\to 1}{\lim }\frac{x^2+2x+1}{x+3}=\frac{4}{4}=1$

再举一例：$\underset{x\to +\infty }{\lim }\frac{2x^2+5x+3}{x^2+3x+5}$
分析：$x\to +\infty$时，分式上下都趋于正无穷，这时无法直接用上述的运算法则。
我们可以通过一些恒等变换，让分式上下的极限都存在，然后再运用上述法则。
分式上下同除以$x^2$，得$\underset{x\to +\infty }{\lim }\frac{2x^2+5x+3}{x^2+3x+5}=\underset{x\to +\infty }{\lim }\frac{2+\frac{5}{x}+\frac{3}{x^2}}{1+\frac{3}{x}+\frac{5}{x^2}}=2$。

3.假设$\underset{x\to x_0}{\lim }g(x)=u$，则$\underset{x\to x_0}{\lim }f[g(x)]=\underset{x\to u}{\lim }f(u)$。

1.2 数列的极限

1.2.1 数列极限的定义

对于一个数列 { a n } \{a_n\} {an​}，若对于$\forall ϵ>0$，$\exists n_0\in {\mathbb{Z}}^{+}$，使$n>n_0$时，$|a_n-A|<ϵ$，则称$A$为数列 { a n } \{a_n\} {an​}的极限。记为：$$\underset{n\to +\infty }{\lim }{a}_n=A$$
也称 { a n } \{a_n\} {an​}收敛于$A$。若数列 { a n } \{a_n\} {an​}无极限，则称 { a n } \{a_n\} {an​}发散。

下面证明$a_n=(-1{)}^n$不是收敛数列：
假设 { a n } \{a_n\} {an​}是收敛数列，那么对于$\forall ϵ>0$，$\exists n_0\in {\mathbb{Z}}^{+}$，使$n>n_0$时，$|a_n-A|<ϵ$。
取$ϵ=\frac{1}{2}$，则在该条件下，$|a_n-A|<\frac{1}{2}$，即$A-\frac{1}{2}<a_n<A+\frac{1}{2}$。
无论$n$有多大，$1$和$-1$都会在 { a n } \{a_n\} {an​}中交替出现，因此我们将$a_n=1$和$a_n=-1$分别代入上式，得：
$A-\frac{1}{2}<-1$且$A+\frac{1}{2}>1$，即$A<-\frac{1}{2}$且$A>\frac{1}{2}$，矛盾！
因此假设不成立， { a n } \{a_n\} {an​}不是收敛数列。

1.2.2 收敛数列的性质

1.收敛数列的极限唯一（反证即可）
2.收敛数列的有界性：若$\underset{n\to +\infty }{\lim }{a}_n=A$，则$\exists M>0,n_0>0$，使$n>n_0$时，有$|a_n|\le M$。
证明：与函数的局部有界性类似，懒得写了（
3.收敛数列的保号性：若$\underset{n\to +\infty }{\lim }{a}_n=A>0$，则$\exists n_0>0$，使$n>n_0$时，有$a_n>0$
证明：取$ϵ=A$（
4.收敛数列的极限与子数列的极限相同。
子数列：假设有一个数列 { a n } \{a_n\} {an​}，有一列正整数$m_1,m_2,...,m_i,...$满足$m_i<m_{i+1}$，那么$a_{m_1},a_{m_2},a_{m_3},...,a_{m_i},...$为数列 { a m } \{a_m\} {am​}的一个子数列。
我们已知$\underset{n\to +\infty }{\lim }{a}_n=A$，想证明$\underset{n\to +\infty }{\lim }{a}_{m_n}=A$。
由$\underset{n\to +\infty }{\lim }{a}_n=A$，可知对于$\forall ϵ>0$，$\exists n_0>0$，当$n>n_0$时，$|a_n-A|<ϵ$。
因为$m_1<m_2<...$且$m_i$均为正整数，所以一定存在$k>0$，使$n>k$时，有$m_n>n_0$。
此时$|a_{m_n}-A|<ϵ$，因此$\underset{n\to +\infty }{\lim }{a}_{m_n}=A$。

由性质4，可以得到一条推论：若某数列有两个子数列收敛于不同的极限，那么该数列不是收敛数列。（逆否命题）
再看$a_n=(-1{)}^n$，我们取$a_{2n-1}$和$a_{2n}$。易知$a_{2n-1}=-1,a_{2n}=1$。
因此$\underset{n\to +\infty }{\lim }{a}_{2n-1}=-1,\underset{n\to +\infty }{\lim }{a}_{2n}=1$，两个子数列的极限不相等。
所以 { a n } \{a_n\} {an​}不是收敛数列。

1.3 无穷小与无穷大

1.3.1 无穷小的定义

无穷小：绝对值可小于任意正数的量（例如$x\to +\infty$时，$-\frac{1}{x}$是无穷小的，$-\frac{1}{x}\to 0$）
无穷大：绝对值可大于任意正数的量（例如$x\to +\infty$时，$x^2$是无穷大的，$x^2\to +\infty$）
0是可以称为无穷小的唯一实数。

1.3.2 无穷量的性质

1.$\underset{x\to x_0}{\lim }f(x)=A$等价于$x\to x_0$时，$f(x)=A+\alpha$，其中$\alpha$是无穷小量。
充分性证明：$\forall ϵ>0,\exists \delta >0$，使$0<|x-x_0|<\delta$时，$|f(x)-A|<ϵ$。取$\alpha =f(x)-A$，则$|\alpha |$可小于任何$ϵ>0$。
因此$\alpha$是无穷小，且$f(x)=A+\alpha$
必要性证明：$x\to x_0$时，$f(x)=A+\alpha$，则$|f(x)-A|=|\alpha |$，由无穷小的定义，对任意正数$ϵ>0$，有$|\alpha |<ϵ$。
因此$\underset{x\to x_0}{\lim }f(x)=A$。

2.无穷小的倒数是无穷大，无穷大的倒数是无穷小（废话）

1.3.3 无穷量的比较

无穷小量都趋于0，但一些无穷小量趋于0的速度更快，另一些无穷小量趋于0的速度更快。
例如，$x\to 0$时，$x^2$比$2x$趋于0的速度更快，$\underset{x\to 0}{\lim }\frac{x^2}{2x}=\underset{x\to 0}{\lim }\frac{x}{2}=0$。
$x\to +\infty$时，$\frac{1}{x^2}$比$\frac{1}{x}$趋于0的速度更快，$\underset{x\to +\infty }{\lim }\frac{\frac{1}{x^2}}{\frac{1}{x}}=\underset{x\to +\infty }{\lim }\frac{1}{x}=0$。
一般地说，假设$\alpha ,\beta$均为无穷小量。
若$\lim \frac{\beta }{\alpha }=0$，则称$\beta$为$\alpha$的高阶无穷小，记作$\beta =o(\alpha )$
若$\lim \frac{\beta }{\alpha }=\infty$，则称$\beta$为$\alpha$的低阶无穷小。
若$\lim \frac{\beta }{\alpha }=c\ne 0$，则称$\beta$为$\alpha$的同阶无穷小。
若$\lim \frac{\beta }{{\alpha }^k}=c\ne 0$，则称$\beta$为$\alpha$的$k$阶无穷小。
若$\lim \frac{\beta }{\alpha }=1$，则称$\beta$为$\alpha$的等价无穷小，记作$\alpha \sim \beta$。
在乘除法中，等价无穷小是可以相互替换的。

例题：已知$x\to 0$，证明$(1+x{)}^{\frac{1}{n}}-1\sim \frac{x}{n}$（谔谔）
法一：
$\underset{x\to 0}{\lim }\frac{(1+x{)}^{\frac{1}{n}}-1}{\frac{x}{n}}=\underset{x\to 0}{\lim }\frac{\frac{1}{n}(1+x{)}^{\frac{1}{n}-1}}{\frac{1}{n}}$（洛！）=$\underset{x\to 0}{\lim }(1+x{)}^{\frac{1}{n}-1}=1$
法二：
注意到$a^n-1=(a-1)(a^{n-1}+a^{n-2}+...+1)$（其实就是等比数列求和公式把$q-1$挪到另一边）
因此$a-1=\frac{a^n-1}{a^{n-1}+a^{n-2}+...+1}$
代入$a=(1+x{)}^{\frac{1}{n}}$得：$(1+x{)}^{\frac{1}{n}-1}=\frac{x}{(1+x{)}^{\frac{n-1}{n}}+(1+x{)}^{\frac{n-2}{n}}+...+(1+x{)}^{\frac{1}{n}}+1}$
于是$\underset{x\to 0}{\lim }\frac{(1+x{)}^{\frac{1}{n}}-1}{\frac{x}{n}}=\underset{x\to 0}{\lim }\frac{x}{(1+x{)}^{\frac{n-1}{n}}+(1+x{)}^{\frac{n-2}{n}}+...+(1+x{)}^{\frac{1}{n}}+1}\ast \frac{n}{x}=\underset{x\to 0}{\lim }\frac{n}{(1+x{)}^{\frac{n-1}{n}}+(1+x{)}^{\frac{n-2}{n}}+...+(1+x{)}^{\frac{1}{n}}+1}$
$=\underset{x\to 0}{\lim }\frac{n}{n}=1$
太麻烦，还是洛必达好（

另：$x\to 0$时，$\cos x-1\sim -\frac{1}{2}{x}^2$
证明：$\underset{x\to 0}{\lim }\frac{\cos x-1}{-\frac{1}{2}{x}^2}=\underset{x\to 0}{\lim }\frac{1-2{\sin }^2\frac{x}{2}-1}{-\frac{1}{2}{x}^2}=\underset{x\to 0}{\lim }\frac{4{\sin }^2\frac{x}{2}}{x^2}=\underset{x\to 0}{\lim }\frac{4(\frac{x}{2}{)}^2}{x^2}=1$。

常用的等价无穷小（

随便挑几个证一下（
令$u=\arcsin x$，则$x=\sin u$。$\underset{x\to 0}{\lim }\frac{\arcsin x}{x}=\underset{x\to 0}{\lim }\frac{u}{\sin u}=1$
$\underset{x\to 0}{\lim }\frac{x-\sin x}{\frac{1}{6}{x}^3}=\underset{x\to 0}{\lim }\frac{1-\cos x}{\frac{1}{2}{x}^2}$（洛！）$=\underset{x\to 0}{\lim }\frac{\sin x}{x}$（洛！）$=1$

1.4 函数的连续性

1.4.1 连续的定义

函数在$x_0$处连续，就是说它的函数图象从$(x_0,f(x_0))$往两边都能延伸。
换句话说，就是在$x_0$附近，$f(x)$都在$f(x_0)$附近。
我们把满足$\underset{x\to x_0}{\lim }f(x)=f(x_0)$的点$x_0$，称为函数在$x_0$处连续。
也可以写成：$\underset{\Delta x\to 0}{\lim }f(x_0+\Delta x)=f(x_0)$
上式$\underset{x\to x_0}{\lim }f(x)=f(x_0)$有三层含义：
1.$f(x)$在$x_0$处有极限
2.$f(x)$在$x_0$处有定义
3.极限值和函数值相等
从连续的定义，我们可以类比左极限和有极限的定义，得到左连续和右连续的定义。
左连续：$\underset{x\to x_0^{-}}{\lim }f(x)=f(x_0)$
右连续：$\underset{x\to x_0^{+}}{\lim }f(x)=f(x_0)$
容易看出连续与左右均连续是等价的。

函数在开区间$(a,b)$连续，那么该函数在$(a,b)$内任意一点连续。
在闭区间$[a,b]$连续，那么在$(a,b)$连续，且在左端点$a$处右连续，右端点$b$处左连续。

下面用定义证明$f(x)=\sin x$在$\mathbb{R}$上连续：
任取一点$x_0$，要证：增量$\Delta x\to 0$时，$\underset{\Delta x\to 0}{\lim }f(x_0+\Delta x)-f(x_0)=0$。
化简：$\underset{\Delta x\to 0}{\lim }\sin (x_0+\Delta x)-\sin x_0=\underset{\Delta x\to 0}{\lim }2\cos (x_0+\frac{\Delta x}{2})\sin \frac{\Delta x}{2}$（和差化积）
$=\underset{\Delta x\to 0}{\lim }2\frac{\Delta x}{2}\cos (x_0+\frac{\Delta x}{2})=\underset{\Delta x\to 0}{\lim }\Delta x\cos (x_0+\frac{\Delta x}{2})$
$\Delta x$是无穷小量，$\cos (x_0+\frac{\Delta x}{2})$是$[-1,1]$内的实数。因此它们之积为无穷小。
所以$\underset{\Delta x\to 0}{\lim }f(x_0+\Delta x)-f(x_0)=0$。

补充和差化积公式：（使用时别漏了系数2）
$\sin \alpha +\sin \beta =2\sin \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2}$。//帅+帅=帅哥
$\sin \alpha -\sin \beta =2\cos \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}$。 //帅-帅=哥帅
$\cos \alpha +\cos \beta =2\cos \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2}$。 //哥+哥=哥哥
$\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}$。//哥-哥=负嫂嫂

1.4.2 间断点

间断，就是不连续；连续，就是不间断（废话
什么情况会导致间断？刚才在连续的定义中，我们提到了三个条件：有极限，有定义，极限与函数值相等。
三个条件只要有一个不满足就会导致间断。因此，间断点有以下几种常见的类型：
可去间断点：存在极限，但没有定义；或者有定义，但极限与函数值不相等。比如$f(x)=x(x\ne 0),f(x)=114514(x=0)$，存在极限$\underset{x\to 0}{\lim }f(x)=0$，但$f(0)=114514\ne 0$。
跳跃间断点：左极限和右极限都存在，但不相等。比如$f(x)=-114514(x<0),f(x)=114514(x\ge 0)$
以上两类称为第一类间断点。（这一类间断点左右极限都存在）

无穷间断点：左极限，右极限至少有一个为无穷。比如$f(x)=\frac{1919810}{x}$。
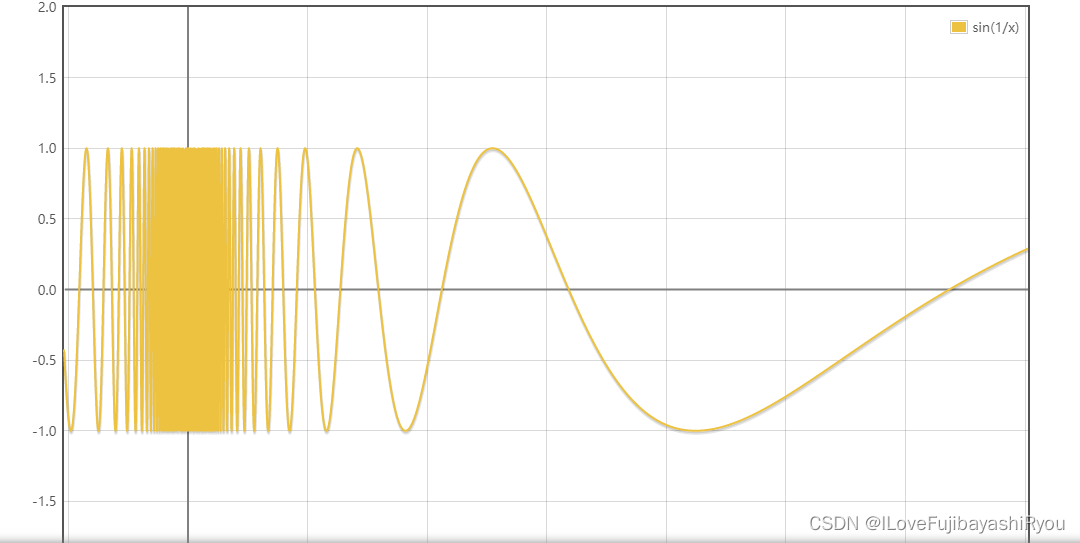
振荡间断点：当自变量趋于某点时，函数值在某个范围内振荡无数次。比如$f(x)=\sin \frac{1}{x}$。
以上两类称为第二类间断点。（这一类间断点左极限、右极限至少有一个不存在）

1.4.3 连续函数的运算

1.两个（在某些区间内）连续的函数的和、差、乘积、商（在这些区间内）都是连续的（作商时要求除数不为0），它们组成的复合函数也是连续的。
这一条性质由极限的运算法则可以轻松推出。
例如$\underset{x\to x_0}{\lim }f(x)+g(x)=\underset{x\to x_0}{\lim }f(x)+\underset{x\to x_0}{\lim }g(x)=f(x_0)+g(x_0)$
$\underset{x\to x_0}{\lim }g(x)=u_0$，则$\underset{x\to x_0}{\lim }f(g(x))=\underset{x\to u_0}{\lim }f(x)=f(u_0)=f(g(x_0))$

2.连续函数$y=f(x)$的反函数$x=f^{-1}(y)$也是反函数。
证明：我们知道，如果连续函数有反函数，那这个连续函数一定是单调的。如果不单调，那么某个函数值可以对应到两个不同的$x$，那么这个函数不可能有反函数。
不妨设$f$单调递增，定义域为$[a,b]$，则值域为$[f(a),f(b)]$。令$x_0\in [a,b]$，$f(x_0)=y_0$。
我们想证明$\underset{y\to y_0}{\lim }x=x_0$，即证$\forall ϵ>0,\exists \delta >0$，在$0<|y-y_0|<\delta$时，$|x-x_0|<ϵ$。分类讨论：
1.当$a\le x_0<a+ϵ$时，取 δ = min ⁡ { y 0 − f ( a ) , f ( x 0 + ϵ ) − y 0 } \delta=\min\{y_0-f(a),f(x_0+\epsilon)-y_0\} δ=min{y0​−f(a),f(x0​+ϵ)−y0​}。
2.当$a+ϵ\le x_0\le b-ϵ$时，取 δ = min ⁡ { y 0 − f ( x 0 − ϵ ) , f ( x 0 + ϵ ) − y 0 } \delta=\min\{y_0-f(x_0-\epsilon),f(x_0+\epsilon)-y_0\} δ=min{y0​−f(x0​−ϵ),f(x0​+ϵ)−y0​}。
3.当$b-ϵ<x_0\le b$时，取 δ = min ⁡ { y 0 − f ( x 0 − ϵ ) , f ( b ) − y 0 } \delta=\min\{y_0-f(x_0-\epsilon),f(b)-y_0\} δ=min{y0​−f(x0​−ϵ),f(b)−y0​}。
这三种情况下，取对应的$\delta$时，均能使$0<|y-y_0|<\delta$时满足$|x-x_0|<ϵ$。
因此$\underset{y\to y_0}{\lim }{f}^{-1}(y)=x_0$，即$f^{-1}$为连续函数。

注：其实连续函数相当于能用一笔画出来的函数，反函数相当于沿直线$y=x$轴对称，如果原函数能一笔画出来，那轴对称后的反函数也能一笔画出来（

3.初等函数在定义区间内都是连续函数。
之所以说“定义区间”，是因为有的初等函数定义域是由离散点组成的，这些离散的点两边没有定义，无法讨论连续性（
比如$y=\sqrt{\sin x-1}$。这个函数有定义时必须有$\sin x-1\ge 0$，即$x=2k\pi +\frac{\pi }{2}$。

1.4.4 连续函数的性质

连续函数显然有极限，那么就满足局部有界性和局部保号性，在1.1.2（
1.有界性与最大值最小值定理：一个函数在闭区间上连续，那么这个函数一定在这个区间内有界，且一定能取到最大值、最小值。

2.零点存在性定理：$f(x)$在$[a,b]$连续，$f(a)f(b)<0$，则$f(x)$在$(a,b)$上有零点。
证明：貌似可以不断二分，如果$f(mid)=0$，那么$mid$就是零点。如果$f(mid)\ne 0$，则看$f(a)f(mid)<0$还是$f(mid)f(b)<0$，分别取区间$[a,mid]$和$[mid,b]$，然后转化为证那个区间内有零点。
（大概也许可能是这样的

3.介值定理：$f(x)$在$[a,b]$连续，且$f(a)\ne f(b)$，则对于 c ∈ [ min ⁡ { f ( a ) , f ( b ) } , max ⁡ { f ( a ) , f ( b ) } ] c\in[\min\{f(a),f(b)\},\max\{f(a),f(b)\}] c∈[min{f(a),f(b)},max{f(a),f(b)}]，一定$\exists \xi \in [a,b]$使$f(\xi )=c$。
证明：令$g(x)=f(x)-c$，则$g(a)g(b)<0$，$g(x)$在$[a,b]$上一定有零点。