棋盘的完美覆盖:
一张8行8列的棋盘一共有64个方格,用一些形状相同的多米诺骨牌覆盖,每一张覆盖相邻的两个方格,没有相互重叠,能用32张这样的多米诺骨牌完全覆盖整张棋盘称为多米诺骨牌完美覆盖或者盖瓦。这样的完美覆盖是存在的,而且不止一种方式,一共有12988816=2^4*17^2*53^2种。那么对于一般的m行n列的棋盘是否存在着多米诺骨牌完美覆盖呢?充要条件是m*n是偶数,这等价于分子物理学中的二聚物问题。有这样的问题:如果把8行8列的棋盘的一条对角线上的两个角的方格去掉,那么完美覆盖还有多少种呢?这样分析:每一张骨牌覆盖相邻的两个方格,那么就假设棋盘是黑白相间的,呈现这样的场景(1代表黑,0代表白):
去掉的两个方格必然是相同的颜色,于是原来32张黑色和32张白色变成了30黑色(白色),32白色(黑色)。如果31张骨诺牌能够完美覆盖,那么就产生了这样的关系式:31(black+white)=30black+32white [or: 30white+32black] 这显然是不成立的。所以一种完美覆盖都不存在。
拓展:如果棋盘的规格是m*n,且一张牌的长度是b(称作b格牌),那么这样的棋盘能够被b格牌完美覆盖吗?显然,想要完美覆盖,b必然是m*n的因子,这就是充分条件:b是m或者n的因子(联系实际)。事实上有这样的结论:m*n的棋盘有b格牌的完美覆盖当且仅当b是m或者n的一个因子。
幻方:
一个由数字1,2,3--n^2组成n行n列的n阶的幻方,满足每一行每一列两条对角线上的数字之和是等值的,假设这样的值是s。那么有这样的等式:n*s=1+2+3+--+n^2=(n^2+1)/2*n^2. -->s=n*(n^2+1)/2. 所以我们可以推断2阶的魔方阵是不存在的,不然s=5啊,显然这是不可能的。幻方的构造和很多方法,n为奇数时有这样一种应用较广的构造方法:首先把1放在第一行的中间,然后按照左下方到右上方的顺序摆放各个数字(行数i和列数j的变化趋势:向量(i-1,j+1)),遇到特殊的情况:
(1)当下一个数字到达已有数字的位置或者四个对角线方向的方阵外时,直接把新的数字放到上一个数字的下面。
(2)当下一个数字的行数到了0时,行数变为n,列数照常加1。
(3)当下一个数字的列数到了n+1时,列数变为1,行数照常减1。
奇数阶幻方(16阶内):
#include"stdio.h"
void xiabiao(int &am







 本文探讨了棋盘的多米诺骨牌完美覆盖问题,揭示了只有当棋盘边长乘积为偶数时存在完美覆盖的充要条件。同时介绍了幻方的概念,通过公式推导和构造方法展示了不同阶幻方的形成,包括奇数阶和偶数阶幻方的构造技巧。
本文探讨了棋盘的多米诺骨牌完美覆盖问题,揭示了只有当棋盘边长乘积为偶数时存在完美覆盖的充要条件。同时介绍了幻方的概念,通过公式推导和构造方法展示了不同阶幻方的形成,包括奇数阶和偶数阶幻方的构造技巧。
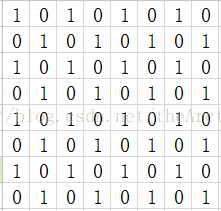
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 637
637

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








