最短路径Djikstra算法 模板+ 例题(九度acm1341: 艾薇儿的演唱会)

最新推荐文章于 2022-09-07 21:31:38 发布
最新推荐文章于 2022-09-07 21:31:38 发布
阅读量5.4k 收藏 1
点赞数
分类专栏： 算法 文章标签： 算法 vector iostream algorithm
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/tmljs1988/article/details/7173666
版权

最短路径Djikstra算法：

主要思想：先找确定的(即当前最短的)，不确定的则动态更新。

从(V-S)集合中找v0到其中最短的路径的顶点，加入到S中并更新(V-S)集合中其他顶点的路径值。

―――――――

参考模板：

Dp初值为v0到某个顶点v的权值weight[ v0][ v],S初值全为false,pre初值全为－1.(Dp,S,pre下标都从1开始)
Dp[ v0]=0;//此行也可以不要,因为下面用Dp[]时总会判断!S[],而S[v0]=TRUE,故Dp[ v0]永远不会被用到

S[ v0]=TRUE;//v0顶点属于S集合
for( int i= 1; i< n; ++i) //注意，下面的循环只需n-1次，将除v0之外的其他所有顶点逐个加入S集合(实际循环时，循环次数可能小于n-1，因为如果在(V－S)集合中找不到从v0可达的点，则会直接跳出：if ( minIndex == -1 )  break)。
 {   min= INFINITY;           

     minIndex= -1;
    for( int k= 1; k<= n; ++k) //求(V-S)集合内与v0距离最近的顶点(Dp[]最小)

     {  if( !S[k] &&min>Dp[k])

        {  minIndex= k;

            min= Dp[ k];

        } 

     }

     if ( minIndex == -1 ){  break;}//此时 (V-S)集合中所有的Dp[]都是无穷大，则表明v0到这些顶点都不可达，故后面的不用再判断了，直接跳出循环

else//选中一个最短且可达点(即Dp[]最小,且不是无穷大)

{  S[ minIndex]= TRUE;//离v0最近的顶点minIndex加入到S集合

   for(int k= 1; k<= n; ++k)    //更新当前最短路径及距离
     {  if( !S[ k] && weight[ minIndex][ k]< INFINITY && Dp[ k]> min+  weight[ minIndex][ k])    //一定要判断weight[ minIndex][ k]< INFINITY，

//否则后面的min+  weight[ minIndex][ k]可能会超出整数的范围而越界，其实应该用减法，因为用加法可能超出整数的范围，if里面只需2个条件即可：if ( !S[ k] && Dp[ k]- min> weight[ minIndex][ k] ) 但这样会不好理解，所以还是可以用上面的3个条件的。       

            {  Dp[ k]= min+ weight[ minIndex][ k];  //修改v0到(V-S)集合中其他顶点的路径长度
                     pre[ k]= minIndex;//minIndex作为桥梁(或中间人),vo与k变得更短,pre记录前一个，以便输出最短路径经过的顶点路径信息(如“1->3->4->2”)
                }
         }

}
 }

―――――

伪代码参考：

Dp[]权值,S[]全false,pre全－1,下标都从1开始

Dp[ v0]=0;S[ v0]=T;

for( i= 1; i< n; ++i)

 {   min= 无穷大; minIndex= -1;

     for( k= 1; k<= n; ++k) //找最短

     {  if( !S[k] && min>Dp[k])

        {  minIndex= k;

            min= Dp[ k];

        } 

     }

     if ( minIndex == -1 ) break;

else

{  S[ minIndex]= T;

   for( k= 1; k<= n; ++k)    //更新

     {  if( !S[ k] && weight[ minIndex][ k]< INFINITY &&

                Dp[ k]> min+  weight[ minIndex][ k])             

            {  Dp[ k]= min+ weight[ minIndex][ k]; 

               pre[ k]= minIndex;

             }

         }

}

}

 

--------------------

加入最短的顶点（dp[]最小）后，更新其他顶点的dp[]，如下图：

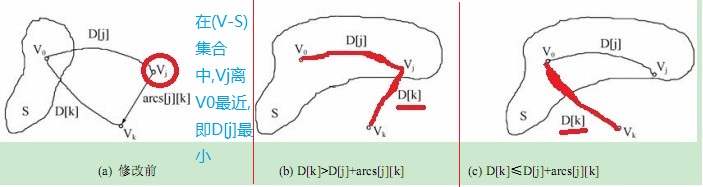
论证：每次从(V-S)集合中找v0到其中最短的路径的顶点v（即Dp[v]最小），Dp[v]为从v0到v的最短路径长度。从v0到v，还有比Dp[v]更短的路径吗？没有了。因为如果还有更短的，则必是经过其他某点vt（属于(V-S)），使Dp[v]> Dp[vt]+ weight[ vt][v]，而Djikstra算法要求权值为正，所以Dp[v]> Dp[vt]，即Dp[v]不是从v0到(V-S)中路径最短的顶点，而路径最短的顶点应该是vt，这与假设（Dp[v]最小）矛盾。

ACM例题：

http://ac.jobdu.com/problem.php?id=1341

九度acm1341: 艾薇儿的演唱会(已AC)

#include <iostream>

#include <memory.h>

#include <algorithm>

#include <vector>

using namespace std;

 

const int MAX_NUM_VERTICES= 101;//最大的节点个数

//const int MAX_NUM_EDGES= 1001;//最大的边个数

const int MAX_INT= 1000000;//最大的整数

 

//查询最短路径并输出

void SearchPathAndPrint( int* pre,  int v0, int v1)

{

       vector< int> viShortestPath;//最短路径的向量

       viShortestPath.push_back( v1);//加入终点

       int iCurr= pre[ v1];

       while( v0 != iCurr)

       {

              viShortestPath.push_back( iCurr);

              iCurr= pre[ iCurr];

       }

       viShortestPath.push_back( v0);//加入起点

 

       输出

       //cout<< v0;

       从某个终点v1开始，根据pre[]从后往前搜索，直到找到起始点v0

       //for ( int i= ( int) viShortestPath.size()- 2; i>= 0 ; --i)

       //{

       //     cout<< "->"<< viShortestPath[ i];

       //}

       //cout<< endl;

}

 

int main()

{

       int n;//节点个数(节点下标从1开始)

       cin>> n;

      

       int iWeight[ MAX_NUM_VERTICES][ MAX_NUM_VERTICES];//一点到另一点的权值

       //memset( iWeight, MAX_INT, MAX_NUM_VERTICES* MAX_NUM_VERTICES* sizeof( int));//初始值为无穷大

 

       for ( int i= 1; i<= n; ++i)

       {

              for ( int j= 1; j<= n; ++j)

              {

                     iWeight[ i][ j]= MAX_INT;

              }

       }

       int iNumEdges;//边的个数

       cin>> iNumEdges;

 

       int v0, vEnd;

       cin>> v0>> vEnd;

 

       int iv1, iv2, iWght;

       for ( int i= 0; i< iNumEdges; ++i)//输入每条边的信息（起点索引，终点索引，边的权值）

       {

              cin>> iv1>> iv2>> iWght;

              if ( iWeight[ iv1][ iv2] > iWght)

              {

                     iWeight[ iv1][ iv2]= iWeight[ iv2][ iv1]= iWght;

              }                  

       }

 

       int iShortestLenFromStart[ MAX_NUM_VERTICES];//连通分量的数组

       bool abSetOK[ MAX_NUM_VERTICES];//已经加入到最短路径组的集合

       int pre[ MAX_NUM_VERTICES];

       /*最短路径中上一个的索引(注:输出时要倒着来,我开始想到用next,但不行,

       因为树的任一节点A只能有一个父节点,但A可同时有几个孩子)*/

      

       memset( iShortestLenFromStart, 0, MAX_NUM_VERTICES* sizeof( int));//初始值为无穷大

       for ( int i= 1; i<= n; ++i)//输入每条边的信息（起点索引，终点索引，边的权值）

       {

              iShortestLenFromStart[ i]= iWeight[ v0][ i];//初始值为权值                         

       }

       //iShortestLenFromStart[ v0]= 0;

      

 

       memset( abSetOK, false, MAX_NUM_VERTICES* sizeof( bool));//初始值为无穷大

       abSetOK[ v0]= true;

 

       memset( pre, -1, MAX_NUM_VERTICES* sizeof( int));//初始值为无穷大

                    

       int iLastInserted= v0;

       int iOutOfSetMin, iOutOfSetMinIndex;//在已加入到最短路径组外的最小值

       for ( int i= 1; i< n; ++i)

       {

              iOutOfSetMin= MAX_INT;

              iOutOfSetMinIndex= -1;

              for ( int w= 1; w<= n; ++w)

              {

                     if ( !abSetOK[ w] && iShortestLenFromStart[ w]< iOutOfSetMin)

                     {

                            iOutOfSetMin= iShortestLenFromStart[ w];

                            iOutOfSetMinIndex= w;

 

                     }//if ( !abSetOK[ w]

              }//for ( int w         

             

              if ( iOutOfSetMinIndex == -1)//如==-1则表明剩下的是孤立的不可达点(即不连通),

//此时 (V-S)集合中所有的Dp[]都是无穷大，故后面的不用再判断了，直接跳出循环

              {

                     break;

              }

              else

              {

                     abSetOK[ iOutOfSetMinIndex]= true;

                     pre[ iOutOfSetMinIndex]= iLastInserted;

                     iLastInserted= iOutOfSetMinIndex;

 

                     for ( int w= 1; w<= n; ++w)

                     {

                            if ( !abSetOK[ w] && iWeight[ iOutOfSetMinIndex][ w]< MAX_INT

                                   && iWeight[ iOutOfSetMinIndex][ w]+ iOutOfSetMin < iShortestLenFromStart[ w])

                            {

                                   iShortestLenFromStart[ w]= iWeight[ iOutOfSetMinIndex][ w]+ iOutOfSetMin;

                                   pre[ w]= iOutOfSetMinIndex;

 

                            }//if ( !abSetOK[ w]

                     }//for ( int w

                    

              }//if ( iOutOfSetMinIndex                  

             

       }//for ( int i

 

       //cout<<"最短的路径为: ";

       SearchPathAndPrint( pre, v0, vEnd);//查询最短路径并输出

 

       cout<< iShortestLenFromStart[ vEnd]<< endl;

 

       //system("pause");

       return 0;

}

tmljs1988
关注
专栏目录
迪杰斯特拉最短路径算法
smoggyxhdz的博客
08-04 2976
问题 A: 算法7-15：迪杰斯特拉最短路径算法 时间限制: 1 Sec  内存限制: 32 MB 题目描述 在带权有向图G中，给定一个源点v，求从v到G中的其余各顶点的最短路径问题，叫做单源点的最短路径问题。 在常用的单源点最短路径算法中，迪杰斯特拉算法是最为常用的一种，是一种按照路径长度递增的次序产生最短路径的算法。 可将迪杰斯特拉算法描述如下： 在本题中，读入一个
基于leetcode743网络的延迟时间 总结图的最短路径问题(djikstra/djikstra+heap/floyd)
weixin_51438023的博客
09-07 259
最短路径问题 最短路径问题是图论中典型的问题，可用于解决管道铺设，线路安装，地图规划等路径问题。我们只需考虑有向图的算法，因为无向图是特殊的有向图，我们可以将所有的无向边u<->v，都拆分成两条有向边：u->v和u<-v，为了方便叙述，我们将图中的点数表示为n，图中的边数表示为m 图的存储 一般有两种存储方式： 邻接矩阵：使用二维数组，w[i] [j]表示点i和点j之间的边权。适用于边数较多的稠密图(当边的数量接近点的数量的平方)使用 //邻接矩阵数组，w[a][b] = c代表
看完就懂了！一篇搞定图论最短路径问题
weixin_30732825的博客
06-26 769
看完就懂了！一篇搞定图论最短路径问题 最最原始的问题——两点间的最短路 这类背景一般是类似：已知各城市之间距离，请给出从城市A到城市B的最短行车方案 or 各城市距离一致，给出需要最少中转方案。 也就是，固定起始点的情况下，求最短路。 这个问题用简单的搜索就能轻松解决。（本部分内容不涉及图论算法，可跳过） 假设用邻接矩阵存图，就比如下面这个例子： 深度优先搜索（dfs）的做法： void d...
C例子：最短路径（dijkstra算法）
10-07
该程序是我写的博客“一起talk C栗子吧（第五十四回：C语言实例--图的最短路径二）”的配套程序，共享给大家使用
最短路径（案例+完整步骤说明+详细注释）
weixin_43624549的博客
03-07 3918
最短路径（案例+步骤说明+详细注释） 步骤： 这道题最应该注意的地方就是路径不是互通的，只能单方向行驶，这就需要多一道步骤：把原地图反过来，即map[i][j]与map[j][i]交换一下，再求i~1的距离的时候，就回到了1到i距离的问题 1~i的最短路径应该怎么求得？ 首先以1为头结点： 1->2：8 1->3：8 1->4：999999(不可直达) 1->5：5 现在得到距离1 节点最近的是节点5，再把节点5作为中间点，看看能不能更新一下1到别的节点的距离： 5
图的最短路径问题
09-02 1367
1. 最短路径问题带权有向图或带权无向图（网络，即网络是不区分方向的）中的每条边都附有一个权值，通常用于表示实际应用中顶点之间关系的某种度量（measure），表示其关联的紧密程度，如： 长度、成本、代价等等 这种长度一般具有可加性，可以看做一个抽象或者泛化的“距离（distance）”；定义：从 vv 到 v′v' 的所有路径中长度最短的路径就是 vv 到 v′v' 的最短路径，最短路径的长度称为
贪心算法单元最短路径：djikstra算法代码
10-23
贪心算法中的Dijkstra算法是一种用于寻找图中两点之间最短路径的经典算法，它适用于有向或无向、加权且边权重非负的图。以下是Dijkstra算法的基本步骤： 1. 初始化：将起始节点的距离设置为0，其他所有节点的距离...
贪心算法单源最短路径:Djikstra算法Java实现
最新发布
10-23
而在单源最短路径问题中，Dijkstra算法是一个经典的求解方法，它适用于带权重的有向图或无向图，目标是从起点到所有其他节点的最短路径。 以下是Dijkstra算法的一个简单的Java实现： ```java import java.util.*; ...
Djikstra算法的代码：此代码成功找到了源节点和目标节点之间的最短路径。-matlab开发
05-29
上面的代码用于通过 Djikstra 算法找到源节点 (A) 到所有给定节点以及非负边权重的特定目标节点之间的最小距离。 其中矩阵m由源节点组成，矩阵n由目的节点组成，w表示连接源和目的边的相应权重。 使用的基本语法如下...
Djikstra算法求解最短路径问题
一只在校程序猿的技术贴
01-25 440
#include <cstdio> #include <algorithm> #include <cstring> #include <vector> using namespace std; const int INF=0x3f3f3f3f; int mp[1001][1001]; int d[1001]; bool vis[1001]; vec...
最短路径算法实例
05-17
一个最短路径算法实例，并包装成文件的输入和输出，需要输入的数据位于in.dat文件，计算结果保存在out.dat文件中
Dijkstra算法求最短路径算法 C++ 经典例题
12-21
本资源是一题经典的例题 用Dijkstra算法求医院的最佳位置
算法题 -- 最短路径
weixin_42836162的博客
09-07 544
华为笔试题
图论最短路径例题
weixin_30872789的博客
04-21 629
一本通网站上不去，截图为证 还是要整博客的。。。 目前学了FloydO（n3）和dijkstra算法O（n2） Floyd是把每个点都遍历一遍，而后者只针对单个起点所以前者慢，但前者可以处理负边权（边的长度）。 下面是一道例题（数据较小用了Floyd）： 中山路上有n（n<=100）家店，每家店的坐标均在-10000~10000之间。其中的m家店之间有通路。若有通路，则表示可以...
最短路径算法（Dijkstra、Bellman-Ford、SPFA、Floyd）
qq_46167487的博客
06-02 423
《算法笔记》笔记 解决最短路径问题的常用算法有Dijkstra、Bellman-Ford、SPFA、Floyd算法。 1、Dijkstra （1） 解决单源最短路问题。即给定图G和起点s，通过算法得到S到达其他每个顶点的最短距离。只能应对所有边权都是非负数的情况， Dijkstra(G,d[],s){ fill(d,d+N,INF); d[s] = 0; for(循环n次）{ u = 使d[u]最小的还未被访问的顶点的编号； 记u已被访问； for(从u出发能到达的所有顶点v）{
Djikstra算法训练——题一：最小花费
qq_45776662的博客
07-08 3379
这是继Dijkstra算法讲解后的第一篇练习题，题目为最小花费，我先上代码，这题跟我们的讲解里的模板题有点类似，但也有很大的不同，可以归为两种题型。代码里我就不注释了。 题目： 【题目描述】 在n个人中，某些人的银行账号之间可以互相转账。这些人之间转账的手续费各不相同。 给定这些人之间转账时需要从转账金额里扣除百分之几的手续费， 请问A最少需要多少钱使得转账后B收到100元。 【输入】 第一行输入两个正整数n,m，分别表示总人数和可以互相转账的人的对数。 以下m行每行输入三个正整数x,y,z， 表示标
最短路径——dj+floyd+spfa（hdu2544）
九日王朝
11-22 865
题目链接： http://acm.hdu.edu.cn/showproblem.php?pid=2544 问题描述： 在每年的校赛里，所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候，却是非常累的！所以现在他们想要寻找最短的从商店到赛场的路线，你可以帮助他们吗？ Input 输入包括多组数据。每组数据第一行是两个整数N、
超级全面的最短路径算法（Bellman-Ford、SPFA、Dijkstra、Floyd）附习题若干
Sheep*的博客
11-21 1064
最短路径算法 1、Bellman-Ford算法的实现及运用 一、知识讲解 Bellman-Ford算法是一种用于求单源最短路径的算法。在此要先讲明何为最短路，顾名思义即为两点间最短的距离。标准定义为：对在权图G=(V,E),（其中V为点集，E为边集）从一个源点s到汇点t有很多路径，其中路径上权和最少的路径，称从s到t的最短路径。如下图（图为无向图）： 该图中A,B间的最短路为A => C =...
第三部分 图论算法 （第三章 最短路路径）例题
蒟蒻こんにゃく
05-04 381
例题一： 单源最短路径 link 思路： 模板，没有什么好讲的。 提醒一下，dij比spfa更加稳定。 Floyed：O(n3)O(n^3)O(n3) = 101510^{15}1015 TLE SPFA: O(nm)O(nm)O(nm)=2∗10102*10^{10}2∗1010 TLE dijkstra:O(nlog⁡(n+m))O(n \log (n+m))O(nlog(n+m)) #include<queue> #include<cstdio> #include<
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值