定理
假设 是复平面上的一个单连通开子集,
是复平面上的一个单连通开子集, 是复平面上有限个点,
是复平面上有限个点, 是定义在
是定义在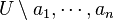 的全纯函数。如果
的全纯函数。如果 是一条把
是一条把 包围起来的可求长曲线,但不经过任何一个
包围起来的可求长曲线,但不经过任何一个 ,并且其起点与终点重合,那么:
,并且其起点与终点重合,那么:
如果γ是若尔当曲线,那么I(γ, ak) = 1,因此:
在这里,Res(f, ak)表示f在点ak的留数,I(γ, ak)表示γ关于点ak的卷绕数。卷绕数是一个整数,它描述了曲线γ绕过点ak的次数。如果γ依逆时针方向绕着ak移动,卷绕数就是一个正数,如果γ根本不绕过ak,卷绕数就是零。
例子
以下的积分
在计算柯西分布的特征函数时会出现,用初等的微积分是不可能把它计算出来的。我们把这个积分表示成一个路径积分的极限,积分路径为沿着实直线从−a到a,然后再依逆时针方向沿着以0为中心的半圆从a到−a。取a为大于1,使得虚数单位i包围在曲线里面。路径积分为:
由于eitz是一个整函数(没有任何奇点),这个函数仅当分母z2 + 1为零时才具有奇点。由于z2 + 1 = (z + i)(z − i),因此这个函数在z = i或z = −i时具有奇点。这两个点只有一个在路径所包围的区域中。
由于f(z)是
f(z)在z = i的留数是:
根据留数定理,我们有:
路径C可以分为一个“直”的部分和一个曲线弧,使得:
因此
如果t > 0,那么当半圆的半径趋于无穷大时,沿半圆路径的积分趋于零:
因此,如果t > 0,那么:
类似地,如果曲线是绕过−i而不是i,那么可以证明如果t < 0,则
因此我们有:
(如果t = 0,这个积分就可以很快用初等方法算出来,它的值为π。)












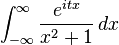




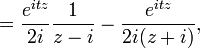






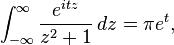















 1095
1095

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








