K-means
已知样本集,其中每一个观测都是d-维实向量 ,K-means要把这m个样本划分到k个集合中(k ≤ m),使得组内平方和(WCSS)最小。
标准算法
最常用的算法使用了迭代优化的技术。它被称为K-means而广为使用,有时也被称为Lloyd算法(尤其在计算机科学领域)。已知初始的k个聚类质心点,算法按照下面两个步骤交替进行。
- 分配(Assignment):将每个样本i分配到聚类中,使得组内平方和(WCSS)达到最小。
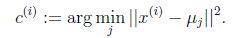
- 更新(Update):对于上一步得到的每一个聚类,以聚类中样本值的图心,作为新的均值点。
![clip_image010[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104061601474753.png)
K-means面对的第一个问题是如何保证收敛,首先可以固定每个类的质心 ,调整每个样本的所属类别
来让WCSS减小;同样固定
,调整每个类的质心
也可以








 本文介绍了计算机视觉中的K-means聚类算法,包括标准流程、Iris数据集应用、欧式距离和随机质心的讨论。同时,文章探讨了最大似然估计的概念,解释了其无法总能得到精确解的原因,并阐述了与最小二乘估计的关系。最后,简要提及了Kullback-Leibler divergence和流形的基本概念。
本文介绍了计算机视觉中的K-means聚类算法,包括标准流程、Iris数据集应用、欧式距离和随机质心的讨论。同时,文章探讨了最大似然估计的概念,解释了其无法总能得到精确解的原因,并阐述了与最小二乘估计的关系。最后,简要提及了Kullback-Leibler divergence和流形的基本概念。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1285
1285

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








