线性回归, 逻辑回归和线性分类器
线性回归, Linear Regression
逻辑回归, Logistic Regression
线性分类器, Linear Classifier
逻辑分类器, Logistic Classifier. 注意, 这个名词是我在文章中为了方便说明问题造出来的.
线性回归可以看作一个Perceptron, 激活函数是identical, 即 f(x)=x .
将逻辑回归也可以看作一个Perceptron, 不同的是使用了sigmoid激活函数.
一般的说法是, 线性回归是真正的回归, 而逻辑回归是一个分类器, 不是真回归. 这算是一个约定俗成的一个失误性命名吗? NO. 逻辑回归的主体还是回归操作: 回归对象是sigmoid函数, 它将输入映射为一个处于0到1之间的小数. 得到这个0到1之间的小数之后人为将其解读成概率, 然后根据事先设定的阈值进行分类. 回归操作的工作量在整个Logistic Regression中保守估计也得超过 99% . 以这个算法的主体---逻辑回归来命名算法是无可厚非的. 当然, 若一定要叫Logistic Classifier也是可以的, 只不过大家都不这么叫而已.
已经有了Logistical Regression, Logistic Classifier, Linear Regression, 很自然的就能想到 Linear Classifier. Logistic Classifier是在Logistic Regression之后加了一步. 虽然Linear Classifier 与Linear Regression 之间没有这种关系, 但它们在形式上还是很相似的:
Logistic Regression(这里特指回归操作):
Logistic Classifier:
Linear Regression:
是不是很具有迷惑性?
可这只是表面现象, 因为Linear Classifier里的 f(x) 并不是通过Linear Regression得到的. 说到这里就得给Linear Classifier下一个定义了. 简单的讲, Linear Classifier就是以超平面(Hyperplane)为决策边界(Decision Boundary)的分类器. 常见的Linear Classifier有Logistic Regression, SVM, Perceptron. 很明显, 这些个分类算法都不是通过Linear Regression 得到自己的分类超平面的。逻辑回归也属于线性分类器,其本质是根据wTx+b的大小来对数据类别进行划分,wTx+b即是代表一个超平面,逻辑回归将wTx+b的值映射到0-1区间,
还有一类经常引起争论的问题: 数据集
D
在原始输入空间
χ
上是线性不可分的, 但将其映射到另外一个空间, 称为特征空间
H
上又成了线性可分的. 例如
χ→H:x→(x,x2,x3)
, 判定函数为
问这个分类器是线性还是非线性的? (其实是使用了kernel)
我个人的看法是: 在特征空间 H 上是线性的, 在原始输入空间 χ 上是非线性的. 如果不指明是哪个空间, 默认为原始输入空间, 为非线性的.
知乎:Logistic Regression是一个单层感知器(Single-Layer Perceptron,或者说单层神经网络),只能对线性可分的数据进行分类。
Back Propagation Network是多层感知器(Multi-Layer Perceptron),可以学到任意复杂的函数。
 可以取两个以上的值,只是Softmax输出值是归一化的概率值。
可以取两个以上的值,只是Softmax输出值是归一化的概率值。
代价函数为:
Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的  个可能值进行了累加。注意在Softmax回归中将
个可能值进行了累加。注意在Softmax回归中将  分类为类别
分类为类别  的概率为:
的概率为:
-
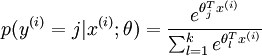 .
.








![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)













 4755
4755











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








