References: 2004_Non-negative matrix factorization with sparseness constraints_JMLR
L1、L2范式
假设需要求解的目标函数为:
E(x) = f(x) + r(x)
其中f(x)为损失函数,用来评价模型训练损失,必须是任意的可微凸函数,r(x)为规范化约束因子,用来对模型进行限制,根据模型参数的概率分布不同,r(x)一般有:L1范式约束(模型服从高斯分布),L2范式约束(模型服从拉普拉斯分布);其它的约束一般为两者组合形式。
L1范式约束一般为:
L2范式约束一般为:
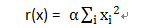
L1范式可以产生比较稀疏的解,具备一定的特征选择的能力,在对高维特征空间进行求解的时候比较有用;L2范式主要是为了防止过拟合。
稀疏性约束
在文章Non-negative Matrix Factorization With Sparseness Constraints中,将L1范式和L2范式组合起来形成新的约束条件,用稀疏度来表示L1范式和L2范式之间的关系:
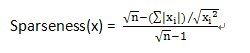
当向量x中只有一个非零的值时,稀疏度为1,当所有元素非零且相等的时候稀疏度为0。n表示向量x的维度。不同稀疏度的向量表示如下:
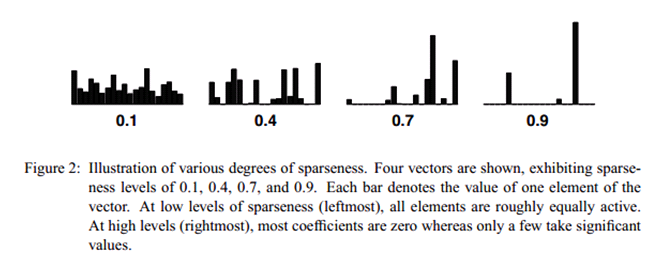
NMF with Sparseness Constraint
目标函数:

算法流程如下:
算法中一个很重要的步骤是投影算法,即给定向量x和L2、L1值,找到给定稀疏度的投影向量。投影算法如下:

算法至多迭代dim(x)次就会收敛,因为每次迭代的时候至少会产生一个新的非零值,所以速度还是很快的。算法的matlab代码在 http://www.cs.helsinki.fi/patrik.hoyer/上,投影部分的python代码如下:
- #!/usr/bin/python
- #-*-coding:utf-8-*-
- from __future__ import division
- import math
- import sys
- #import numpy
- """desiredsparseness can be set [0.1,0.2,0.3,0.4,0.5]"""
- def l1sparse(dimension,desiredsparseness):
- return math.sqrt(dimension) - (math.sqrt(dimension)-1)*desiredsparseness
- def vsum(vector):
- sum =








 本文探讨了非负矩阵分解(NMF)中结合L1和L2范式的稀疏性约束。通过引入稀疏度概念,优化目标函数以达到特定稀疏程度。文章介绍了L1范式用于产生稀疏解,防止过拟合,而L2范式确保模型稳定。算法包括投影步骤,以找到满足约束的向量。提供了相应的MATLAB和Python代码实现。
本文探讨了非负矩阵分解(NMF)中结合L1和L2范式的稀疏性约束。通过引入稀疏度概念,优化目标函数以达到特定稀疏程度。文章介绍了L1范式用于产生稀疏解,防止过拟合,而L2范式确保模型稳定。算法包括投影步骤,以找到满足约束的向量。提供了相应的MATLAB和Python代码实现。
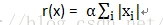

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 486
486

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








