torch.optim.Adam算法里面参数的含义

[docs]class Adam(Optimizer):
    r"""Implements Adam algorithm.

    It has been proposed in `Adam: A Method for Stochastic Optimization`_.
    The implementation of the L2 penalty follows changes proposed in
    `Decoupled Weight Decay Regularization`_.

    Arguments:
        params (iterable): iterable of parameters to optimize or dicts defining
            parameter groups
        lr (float, optional): learning rate (default: 1e-3)
        betas (Tuple[float, float], optional): coefficients used for computing
            running averages of gradient and its square (default: (0.9, 0.999))
        eps (float, optional): term added to the denominator to improve
            numerical stability (default: 1e-8)
        weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
        amsgrad (boolean, optional): whether to use the AMSGrad variant of this
            algorithm from the paper `On the Convergence of Adam and Beyond`_
            (default: False)

    .. _Adam\: A Method for Stochastic Optimization:
        https://arxiv.org/abs/1412.6980
    .. _Decoupled Weight Decay Regularization:
        https://arxiv.org/abs/1711.05101
    .. _On the Convergence of Adam and Beyond:
        https://openreview.net/forum?id=ryQu7f-RZ
    """

lr 是Adam算法里面的,代表学习率

betas ，一个元组（tuple）是Adam算法里面的和，代表历史积累动量在新求的的动量里面的权重比

eps，是Adam算法里面的，避免分母为零用的，不会影响结果的小tip

weight_decay，就是第12行里面的，就是weight参数的衰减因子，因为和都大于0，每次update weight参数，

都会对参数的值增加起到抑制的作用。

那么为什么要抑制weight参数不要变得过大呢？

从模型的复杂度上解释：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合更好（这个法则也叫做奥卡姆剃刀）

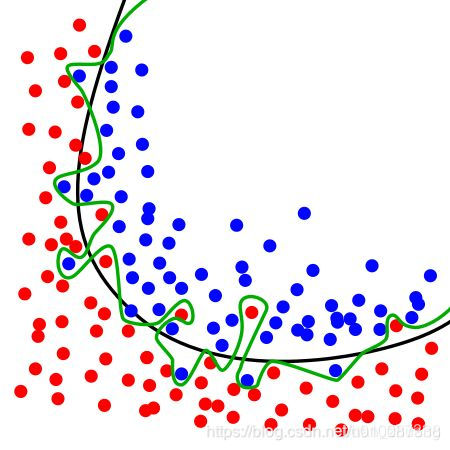
其实控制weight参数在一个值范围内，也在一定程度上减小了function set的选择范围，不会让我们选择一个过于偏冷复杂的function如下图，

训练时我们选择简单的黑线就挺好，不必找到最合适但很复杂的绿线。