要点: Jensen不等式。函数的期望,大于等于期望的函数,对于凸函数,E(f(x))>=f(E(x))。
如果是凹函数,不等号方向相反,E(f(x))<=f(E(x))。
EM算法只能求得局部极值点
---------------------
EM和坐标上升的区别:如果是坐标上升,其实是固定一部分参数,另一部分参数求导等于0,交替进行优化,
首先EM中的似然函数,不可直接对Z和θ求导。切记EM中求得是Z的条件概率分布,也就是后验,正比于联合概率,p(z|x,θ)=p(z,x|θ)/p(x|θ)。p(z,x|θ)=p(x|z,θ)*p(z)然后优化θ,最大化ELBO。
然后优化θ,最大化ELBO。
MLE是似然,MAP最大后验概率,也就是最大化似然乘以先验,。
联合概率等于似然乘以先验,后验概率正比于似然乘以先验。
什么是似然?p(X)?还是p(X|θ)?应该是后者,这里把θ当做点,而不是随机变量,
而把隐变量z当做随机变量,所以p(X)=sum p(X,z),在z上展开。。
我迷茫的是,p(z|x,θ)何求???p(z,x|θ)=p(x|z,θ)*p(z),难道用似然乘以先验??并没有什么先验啊,举的例子都是混合高斯,直接用MLE离散估计。
记住M步,需要优化的公式,是sum Q(z)logP(z,x)
样本越多,先验越不重要,
--------------------
Jensen不等式在证明的时候注意,
f=log 是凹函数,g=p/q,,g是关于z的函数,E=q(z),z上的一个分布
f(E(g{z}))<=E(f(g{z})),,需要注意的是g是关于z的函数,而不是个简单的自变量。theta和x都确定,
对于zi,或者函数g(zi),q(zi)给出一个权重概率。
theta对于整个似然目标函数是自变量。
以后在用jensen不等式时候,只需要外层选取一个凸函数凹函数即可,没必要选取整个函数。
EM证明的大致思路:
1,构造观测变量的对数似然函数,2,然后在隐变量z上全概率公式展开,并添加关于z的分布函数Q,3,利用jensen不等式构造下界。4,下界是关于theta和z的分布Q的函数,先固定theta,使得下界最大,也就是等号成立,(固定theta后,l(theta),也是常数)。有如下等式
求得使得等号成立的Q,也就是z,服从x,theta的后验条件概率。
与联合概率分布成正比的分布是后验分布
通常x选择的不同,那么q(z)正比于p(x,z)的成分就不同,每个x确定一组p(x,z),,也表达了后验的本质,根据x选择z的比例成分。即后验概率。
5,注意下界函数是关于z的分布和theta的函数,现在有了z的分布Q,在去选择最大的theta。如此迭代。
注意是求z的分布Q,不要说成z的期望。是对数似然在z分布上的期望,不是z的期望。
如下高斯混合模型,半监督学习。E步,计算的是样本混合高斯成分,也就是隐变量的分布,而不是期望。
EM中的下界,也是变分算法里面的ELOB。
EM中是logp(x)>=ELOB,变分算法中是logp(x)=ELOB+KL(q||p)
ELOB = E(logp(x,z))-E(logq(z)),,其中E是在q(z)上的期望。。ELOB= evidence lower bound,证据下界,证据就是观测变量x
-----------------------------------------------------------------------
EM与变分的区别(个人观点)
求logp(x)最大化,是求 
很显然当前θ下,要想ELOB最大化,也就是KL最小为0,也就是q(X)等于p(Z|X,θ)。
区别在于是否可求p(Z|X,θ)。
与联合概率分布成正比的分布是后验分布
所以求ELOB关于θ的最大值,但当θ再次变动时,就又得改变q(x)。如此反复。
-----------------------------------------------------------------------------------------------------
链接:https://www.zhihu.com/question/27976634/answer/163164402
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1. **为什么要有EM算法**
我把EM算法当做最大似然估计的拓展,解决难以给出解析解的最大似然估计(MLE)问题。考虑高斯分布,它的最大似然估计是这样的:
 (1)
(1)
其中,  ,
,  ,
,  是对数似然函数,分号左边是随机变量,右边是模型参数。
是对数似然函数,分号左边是随机变量,右边是模型参数。  表示X的概率值函数,它是一个以
表示X的概率值函数,它是一个以  为参数的函数(很多人看不懂EM算法就是因为符号问题)。这里对
为参数的函数(很多人看不懂EM算法就是因为符号问题)。这里对  求导很容易解出
求导很容易解出  。
。
如果这是个含有隐量Z的模型比如混合高斯模型,  (2)
(2)
上面假设共有K个高斯模型混合.每个高斯模型的参数为 ,每个高斯模型占总模型的比重为
 。隐变量
。隐变量  表示样本
表示样本  来自于哪一个高斯分布。分布列为:P(Z=
来自于哪一个高斯分布。分布列为:P(Z=  )=
)= 
P(Z=  )=
)= 
...
P(Z=  )=
)= 
可以认为,混合高斯分布的观测值是这样产生的:先以概率  抽取一个高斯分布
抽取一个高斯分布  ,再以该高斯分布
,再以该高斯分布  去生成观测x。其实这里的
去生成观测x。其实这里的  就是Z的先验分布
就是Z的先验分布  (这里特地加上;
(这里特地加上;  表示P(Z)的参数是
表示P(Z)的参数是  ,你需要求出
,你需要求出  才能表示这个先验分布),而
才能表示这个先验分布),而  就是给定Z下的条件概率
就是给定Z下的条件概率  这时,令
这时,令  ,
,  , 最大似然估计成了
, 最大似然估计成了  (3)
(3)
据群众反映,求和、取对数、再求和,这种形式求偏导较为费劲(其实也没那么费劲。。。EM算法并不是专门为混合高斯模型服务的,其他情况更加费劲)要是能把log拿到  里层就好了,直接对最里层的式子求偏导岂不快哉?于是就有了EM算法
里层就好了,直接对最里层的式子求偏导岂不快哉?于是就有了EM算法
2. **为什么叫E步和M步**
为了解决这个问题,有人想到了Jensen(琴生)不等式. log是个凹函数,以隐变量Z的任一函数 f(Z) 举个例子: ![logE[f(Z)]=log\sum_Z P(Z)f(Z) \geq \sum_Z P(Z)logf(Z)=E[logf(Z)]](https://i-blog.csdnimg.cn/blog_migrate/f770a92babe50865a7bd7e5919f0a753.png) (4)
(4)
根据琴生不等式的性质,当随机变量函数 f(Z) 为常数时,不等式取等号。上式中的期望换成条件期望,分布 P(Z) 换成条件分布也是一样的。注意(3)中的联合分布  在执行
在执行  时可以把X看做是定值,此时我们可以把这个联合分布当做Z的随机变量函数(它除以Q(Z)当然还是Z的随机变量函数)来考虑,并且引入一个关于Z的分布Q(Z),具体是啥分布还不清楚,可能是给定某某的条件分布,只知道它是一个关于
时可以把X看做是定值,此时我们可以把这个联合分布当做Z的随机变量函数(它除以Q(Z)当然还是Z的随机变量函数)来考虑,并且引入一个关于Z的分布Q(Z),具体是啥分布还不清楚,可能是给定某某的条件分布,只知道它是一个关于  的函数:
的函数: ![\begin{aligned} Max &=\max_\theta \sum_X log \sum_ZP(X,Z;\theta) \\ &=\max_\theta \sum_X log \sum_Z Q(Z;\theta) \cdot \frac{P(X,Z;\theta)}{Q(Z;\theta)} \\ &=\max_\theta \sum_X log E_Q[\frac{P(X,Z;\theta)}{P(Z;\theta)}] \\ &\geq \max_\theta \sum_X E_Q[log \frac{P(X,Z;\theta)}{Q(Z;\theta)}] \\ &= \max_\theta \sum_X \sum_Z Q(Z;\theta) log \frac{P(X,Z;\theta)}{Q(Z;\theta)} \end{aligned}](https://i-blog.csdnimg.cn/blog_migrate/95448671c6aa503e210dbd3eda89486c.png) (5)
(5)
只有当  (c为任意常数)(6) ,
(c为任意常数)(6) ,
式(5)才能取等号,注意到Q是Z的某一分布,有  这个性质,因此
这个性质,因此  (7)
(7)
所以只需要把Q取为给定X下,Z的后验分布,就能使式(5)取等号,下一步只需要最大化就行了.这时(5)为  (8)
(8)
其中:  (9)
(9)  (10)
(10)
好吧,直接对  求导还是很麻烦,不过已经可以用迭代来最大化啦。
求导还是很麻烦,不过已经可以用迭代来最大化啦。
1)先根据式(10),由  求后验分布
求后验分布 
2)再把  带入(8)中,
带入(8)中,  (11)
(11)
这就只需要最大化联合分布  了,最大化求出
了,最大化求出  后再重复这2步。
后再重复这2步。
M步很显然,就是最大化那一步,E步又从何谈起呢?根据式(11)有 ![\begin{aligned} \theta^{(j+1)} &= \arg\max_\theta \sum_X \sum_Z Q^{(j)} log P(X,Z;\theta) \\ &= \arg\max_\theta \sum_X E_{Q^{(j)}} [log P(X,Z;\theta)] \\ &= \arg\max_\theta \sum_X E_{Z|X;\theta^{(j)}} [log P(X,Z;\theta)] \\ &= \arg\max_\theta \sum_X E_Z [log P(X,Z;\theta)|X;\theta^{(j)}] \end{aligned}](https://i-blog.csdnimg.cn/blog_migrate/f1b8220a708f59e162fadad47dc98bec.png) 其实,E步就是求给定X下的条件期望,也就是后验期望,使得式(5)的琴生不等式能够取等号,是对琴声不等式中,小的那一端进行放大,使其等于大的那一端,这是一次放大;M步最大化联合分布,通过0梯度,拉格朗日法等方法求极值点,又是一次放大。只要似然函数是有界的,只要M步中的0梯度点是极大值点,一直放大下去就能找到最终所求。
其实,E步就是求给定X下的条件期望,也就是后验期望,使得式(5)的琴生不等式能够取等号,是对琴声不等式中,小的那一端进行放大,使其等于大的那一端,这是一次放大;M步最大化联合分布,通过0梯度,拉格朗日法等方法求极值点,又是一次放大。只要似然函数是有界的,只要M步中的0梯度点是极大值点,一直放大下去就能找到最终所求。
-----------------------------------------------------------------------------------
现在,通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布,我们通过最大化其似然函数,就可以得到了对应高斯分布的参数θ=[u,∂]T了。那么,对于我们学校的女生的身高分布也可以用同样的方法得到了。
再回到例子本身,如果没有“男的左边,女的右边,其他的站中间!”这个步骤,或者说我抽到这200个人中,某些男生和某些女生一见钟情,已经好上了,纠缠起来了。咱们也不想那么残忍,硬把他们拉扯开。那现在这200个人已经混到一起了,这时候,你从这200个人(的身高)里面随便给我指一个人(的身高),我都无法确定这个人(的身高)是男生(的身高)还是女生(的身高)。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的,还是女生的那个身高分布抽取的。用数学的语言就是,抽取得到的每个样本都不知道是从哪个分布抽取的。
这个时候,对于每一个样本或者你抽取到的人,就有两个东西需要猜测或者估计的了,一是这个人是男的还是女的?二是男生和女生对应的身高的高斯分布的参数是多少?
只有当我们知道了哪些人属于同一个高斯分布的时候,我们才能够对这个分布的参数作出靠谱的预测,例如刚开始的最大似然所说的,但现在两种高斯分布的人混在一块了,我们又不知道哪些人属于第一个高斯分布,哪些属于第二个,所以就没法估计这两个分布的参数。反过来,只有当我们对这两个分布的参数作出了准确的估计的时候,才能知道到底哪些人属于第一个分布,那些人属于第二个分布。
这就成了一个先有鸡还是先有蛋的问题了。鸡说,没有我,谁把你生出来的啊。蛋不服,说,没有我,你从哪蹦出来啊。(呵呵,这是一个哲学问题。当然了,后来科学家说先有蛋,因为鸡蛋是鸟蛋进化的)。为了解决这个你依赖我,我依赖你的循环依赖问题,总得有一方要先打破僵局,说,不管了,我先随便整一个值出来,看你怎么变,然后我再根据你的变化调整我的变化,然后如此迭代着不断互相推导,最终就会收敛到一个解。这就是EM算法的基本思想了。
假设我们有一个样本集 {x(1),…,x(m)} ,包含 m 个独立的样本。但每个样本 i 对应的类别 z(i) 是未知的(相当于聚类),也即隐含变量。故我们需要估计概率模型 p(x,z) 的参数 θ ,但是由于里面包含隐含变量 z ,所以很难用最大似然求解,但如果 z 知道了,那我们就很容易求解了
对于参数估计,我们本质上还是想获得一个使似然函数最大化的那个参数θ,现在与最大似然不同的只是似然函数式中多了一个未知的变量z,见下式(1)。也就是说我们的目标是找到适合的θ和z让L(θ)最大。那我们也许会想,你就是多了一个未知的变量而已啊,我也可以分别对未知的θ和z分别求偏导,再令其等于0,求解出来不也一样吗?

本质上我们是需要最大化(1)式(对(1)式,我们回忆下联合概率密度下某个变量的边缘概率密度函数的求解,注意这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和,也就得到等式左边为随机变量x的边缘概率密度),也就是似然函数,但是可以看到里面有“和的对数”,求导后形式会非常复杂(自己可以想象下log(f1(x)+ f2(x)+ f3(x)+…)复合函数的求导),所以很难求解得到未知参数z和θ。那OK,我们可否对(1)式做一些改变呢?我们看(2)式,(2)式只是分子分母同乘以一个相等的函数,还是有“和的对数”啊,还是求解不了,那为什么要这么做呢?咱们先不管,看(3)式,发现(3)式变成了“对数的和”,那这样求导就容易了。我们注意点,还发现等号变成了不等号,为什么能这么变呢?这就是Jensen不等式的大显神威的地方。
Jensen不等式:
设f是定义域为实数的函数,如果对于所有的实数x。如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。当x是向量时,如果其hessian矩阵H是半正定的,那么f是凸函数。如果只大于0,不等于0,那么称f是严格凸函数。
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X])
现在我们就需要一点想象力了,上面的式(2)和式(3)不等式可以写成:似然函数L(θ)>=J(z,Q),那么我们可以通过不断的最大化这个下界J,来使得L(θ)不断提高,最终达到它的最大值。

见上图,我们固定θ,调整Q(z)使下界J(z,Q)上升至与L(θ)在此点θ处相等(绿色曲线到蓝色曲线),然后固定Q(z),调整θ使下界J(z,Q)达到最大值(θt到θt+1),然后再固定θ,调整Q(z)……直到收敛到似然函数L(θ)的最大值处的θ*。
假定有训练集{x(1), x(2), …, x(m)},包含m个独立样本,希望从中找到该组数据的模型p(x,z) 的参数,这里z是模型的隐变量。
然后还是老样子写出对数似然函数:
接下来就是高斯式解释了,注意看:
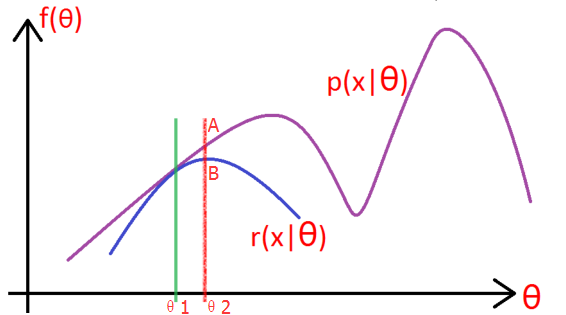
如上图所示,紫色的线是我们的目标模型p(x| θ) 的曲线。
1, 因为这个模型含有隐变量z,所以为了消除z的影响,就先做一个除了不含有z模型:r(x| θ),使得r(x| θ) ≤ p(x| θ)。(你先别管这个r怎么得到,方法之后会说,反正总能给一个r满足这个条件吧!),取一个值令 r(x|θ1) = p(x|θ1),如绿线所示,然后对r(x| θ) 求极大似然,得到r的极值点B,和此时r的参数 θ2,如红线所示。
2, 这一步上图没有给出,就是:将r的 参数从θ1变成θ2,此时r的图像就向右上方移动,与p相交于A,此时仍然有r≤p。
3, 重复第二步和第三部,知道收敛。
PS:从上图可以看出,EM算法只能求得局部极值点。














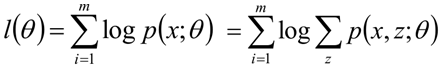














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








