数据挖掘基础知识-矩阵(分解)

1. 矩阵知识：

//特征值，行列式，秩，对称矩阵，单位矩阵，正定半正定，雅可比等等！！

正交矩阵：

如果：AA'=E（E为单位矩阵，A'表示“矩阵A的转置矩阵”。）或A′A=E，则n阶实矩阵A称为正交矩阵， 若A为正交阵，则满足以下条件:

1) A ^T是正交矩阵

2)  （E为单位矩阵）

3) A的各行是单位向量且两两正交

4) A的各列是单位向量且两两正交

5) (Ax,Ay)=(x,y) x,y∈R

6) |A| = 1或-1

 

 

 

2. 矩阵分解（推荐系统）基本思想：

矩阵分解的思想简单来说就是每一个用户和每一个物品都会有自己的一些特性，用矩阵分解的方法可以从评分矩阵中分解出用户——特性矩阵，特性——物品矩阵，这样做的好处一是得到了用户的偏好和每件物品的特性，二是见底了矩阵的维度。图示如下：

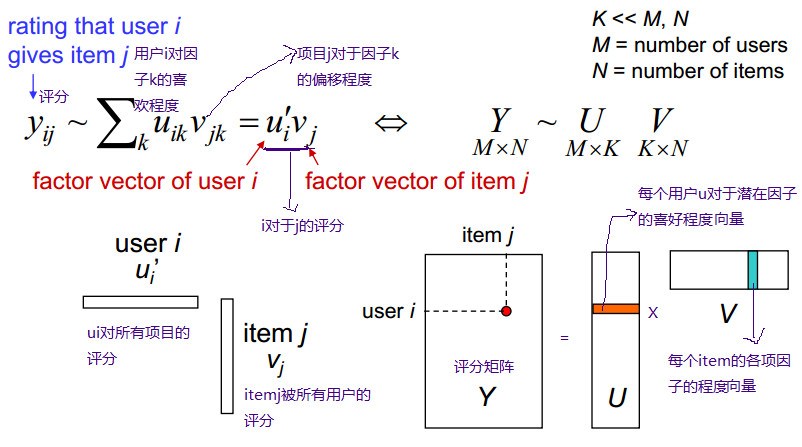
用用户对电影来举例子就是：每个用户看电影的时候都有偏好，这些偏好可以直观理解成：恐怖，喜剧，动作，爱情等。用户——特性矩阵表示的就是用户对这些因素的喜欢程度。同样，每一部电影也可以用这些因素描述，因此特性——物品矩阵表示的就是每一部电影这些因素的含量，也就是电影的类型。这样子两个矩阵相乘就会得到用户对这个电影的喜欢程度。

 

 

---------------------------------------------------------------------------------------------------------------------------

SVD分解：

假设M是一个m×n阶矩阵，其中的元素全部属于域 K，也就是 实数域或复数域。如此则存在一个分解使得

M = UΣV*，

其中U是m×m阶酉矩阵；Σ是半正定m×n阶对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。

在矩阵M的奇异值分解中 M = UΣV*

·U的列(columns)组成一套对M的正交"输入"或"分析"的基向量。这些向量是MM*的特征向量。

·V的列(columns)组成一套对M的正交"输出"的基向量。这些向量是M*M的特征向量。

·Σ对角线上的元素是奇异值，可视为是在输入与输出间进行的标量的"膨胀控制"。这些是M*M及MM*的奇异值，并与U和V的行向量相对应

matlab code：

     

>> A

A =

     1     2     3     4     5
     4     3     2     1     4

>> [u,s,v] = svd(A);
>> u

u =

   -0.7456   -0.6664
   -0.6664    0.7456

>> s

s =

    9.5264         0         0         0         0
         0    3.2012         0         0         0

>> v

v =

   -0.3581    0.7235   -0.2591   -0.1658   -0.5038
   -0.3664    0.2824    0.2663    0.8031    0.2647
   -0.3747   -0.1587    0.8170   -0.2919   -0.2858
   -0.3830   -0.5998   -0.3560    0.3230   -0.5123
   -0.6711   -0.1092   -0.2602   -0.3714    0.5762

 

SVD与推荐系统：（http://blog.csdn.net/wuyanyi/article/details/7964883）

-------------------------------------------------------------------------------------

直观地说：

假设我们有一个矩阵，该矩阵每一列代表一个user，每一行代表一个item。

如上图，ben,tom....代表user，season n代表item。

矩阵值代表评分（0代表未评分）：

如 ben对season1评分为5，tom对season1 评分为5，tom对season2未评分。

机器学习和信息检索：

机器学习的一个最根本也是最有趣的特性是数据压缩概念的相关性。

如果我们能够从数据中抽取某些有意义的感念，则我们能用更少的比特位来表述这个数据。

从信息论的角度则是数据之间存在相关性，则有可压缩性。

SVD就是用来将一个大的矩阵以降低维数的方式进行有损地压缩。

降维：

下面我们将用一个具体的例子展示svd的具体过程。

首先是A矩阵。

A =

     5     5     0     5
     5     0     3     4
     3     4     0     3
     0     0     5     3
     5     4     4     5
     5     4     5     5
（代表上图的评分矩阵）

使用matlab调用svd函数：

[U,S,Vtranspose]=svd(A)

U =
   -0.4472   -0.5373   -0.0064   -0.5037   -0.3857   -0.3298
   -0.3586    0.2461    0.8622   -0.1458    0.0780    0.2002
   -0.2925   -0.4033   -0.2275   -0.1038    0.4360    0.7065
   -0.2078    0.6700   -0.3951   -0.5888    0.0260    0.0667
   -0.5099    0.0597   -0.1097    0.2869    0.5946   -0.5371
   -0.5316    0.1887   -0.1914    0.5341   -0.5485    0.2429

S =
   17.7139         0         0         0
         0    6.3917         0         0
         0         0    3.0980         0
         0         0         0    1.3290
         0         0         0         0
         0         0         0         0

Vtranspose =