高斯分布
我们将用整个第2章介绍各种概率分布的研究以及他们的主要属性。但是,这里介绍连续变量最重要的概率分布即正态或高斯分布是比较合适的。在本章的其余部分我们将广泛使用这种分配,实际上贯穿本书的许多地方。
在一个实值变量x的情况下,高斯分布定义如下:
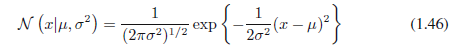
它由两个参数:μ称为平均值和σ2称为方差控制。方差的平方根σ叫做标准差,方差的倒数(β= 1 /σ2)叫做精度。我们不久将看到这些项的动机。图1.13显示了一个高斯分布。
从(1.46)的形式我们可以看到高斯分布满足:

另外它也明确地表明高斯分布被归一化,所以
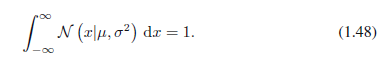
(1.46)满足有效概率密度的两个要求。
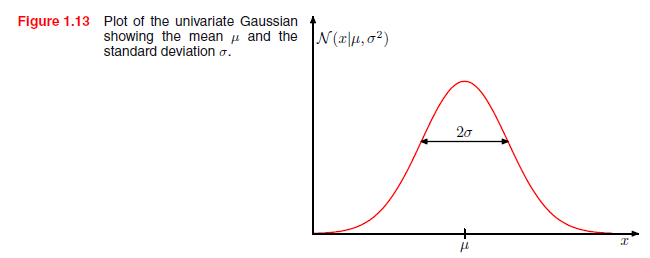
我们可以容易的找到高斯分布下x函数的期望。x的平均值如下:
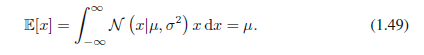
因为参数μ表示x的平均值,它被称作均值。类似的,对于二阶的情况:
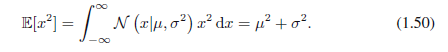
从(1.49)和(1.50),得到x的方差:
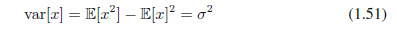
因此σ2叫做方差。一个分布的最大值叫做它的模式。对高斯来说,它的模式和均值一致。
我们也对定义在连续变量的D维向量x的高斯分布感兴趣,其形式如下:
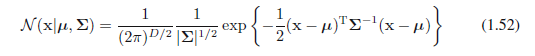
其中D维向量μ叫做均值,D ×D矩阵 Σ叫做协方差,|Σ| 表示Σ的行列式。它的性质在2.3节会详细讨论,但在本章我们将简短的使用多元高斯分布。
现在假设我们有观测X=(x1,,,xn)T的一个数据集,X代表标量x的N个观测值。注意,我们使用打印字体X来区分单个矢量值变量(x1,…,xD)T的观测值,用x表示。我们将假设观测是从均值μ和方差σ2未知的高斯分布中独立抽取出来的,并且我们想从数据集中确定这些参数。从相同分布中独立抽取出的数据点是独立同分布的,通常缩写为i.i.d。我们可以看出,两个独立事件的联合概率由每个事件的边缘概率乘积得到。因为我们的数据集x是独立同分布的,因此,给出μ和σ2,我们可以将数据集的概率写为下面的形式:
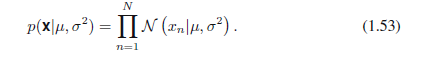
当把它看做μ和σ2的函数时,该等式就是高斯分布的似然函数,粗略地图像解释如1.14。
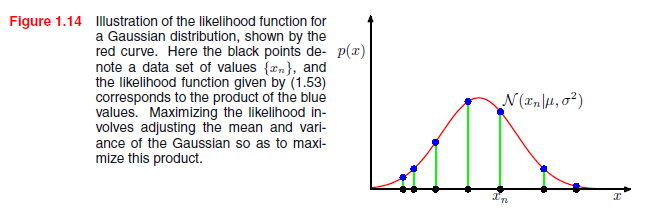
使用观测数据集来确定概率分布中的参数有一个普遍的标准,即找到最大化似然函数的参数值。这似乎是一个奇怪的标准,因为根据我们前面概率论的讨论,似乎更自然的做法是给定数据最大化参数的概率,而不是给定参数最大化数据的概率。事实上,这两个标准是相关的,我们将在曲线拟合的情况下讨论。
然而,目前我们应通过最大化似然函数(1.53)来确定高斯中未知参数μ和σ2的值。在实践中,更方便的是最大化似然函数的对数。因为对数是单调递增函数,最大化函数的对数相当于最大化函数本身。取对数不仅简化了随后的数学分析,也有利于用数字表示,因为许多小概率求积容易溢出计算机的数值精度,通过转化为计算对数概率的和可以解决这个问题。从(1.46)和(1.53),对数似然函数可以写成如下形式:
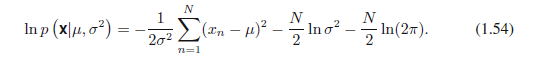
对μ最大化(1.54),我们得到了最大似然解决方案:

它是样本均值,即观察值{x}的均值。类似地,对σ2最大化(1.54),我们得到了方差的最大似然解决方案:
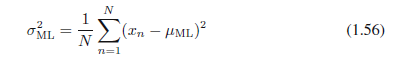
它是相对于样本均值μML的样本方差。注意我们正在执行对于μ和σ2的联合最大化。但是在高斯分布的情况下,μ的解决方法从σ2的解决方法中分离出来,使得我们可以先估计(1.55),紧接着用它的结果来估计(1.56)。
在本章的后面以及随后的章节中,我们将突出最大似然方法显著的局限性。这里,我们给出问题的一个指示,这个问题出现在单变量高斯分布最大似然参数设置解上。特别是,我们将展示最大似然方法系统地低估了分布的方差。这是被称为偏差现象的一个例子,并且和多项式曲线拟合情况下遇到过度拟合相关。我们首先注意到最大似然解μML和σ2ML是数据集x1,, ,xn的函数。考虑这些量对于数据集的期望,表示如下:
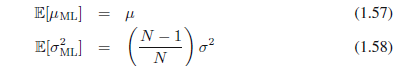
通常最大似然估计将获得正确的均值,但是用于因子(N − 1)/N而低估了真正的方差。这个结果的直观感受如图1.15

根据(1.58),下面的方差参数估计是无偏差的:
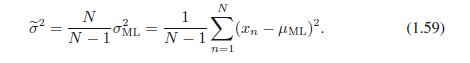
在10.1.3节,我们将会看到当我们采取贝叶斯方法时,这个结果是如何自动出现的。
注意,随着数据点的数量N逐渐变大,最大似然解的偏压变得不那么明显,并且在Ñ→∞时,方差的最大似然解等于分布的真实方差。在实践中,对于任何小N的情况,这种偏见被证明不是一个严重的问题。然而,在整本书中,我们对更复杂的且带有很多参数的模型感兴趣,这些模型中与最大似然相关的偏差问题会更加严重。事实上,正如我们将要看到的,最大似然问题中的偏差问题根源在于过拟合问题,该问题就是我们前面多项式曲线拟合情况下遇到的。






















 638
638

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








