PRML-系列一之1.1

实例：多项式曲线拟合
　　我们首先介绍一个简单的回归问题，我们将其作为本章的实例来引出一些关键的概念。假设我们观察到一个实际的输入变量x，我们希望用这个观察值来预测实际的目标变量t。为了表示，一种有益 的方式是：考虑用综合产生的数据得到的例子，因为该过程产生的数据与其他学习模型比较后我们可以知道精确的过程。本例中的数据是从带有随机噪声的函数sin（2πx）产生，如附件A中详细的描述。
　　现在假设我们有一个训练集，包括N个观测值，写作x≡（x1，…，xN）T，以及对应的观测T，表示为（t1，，，tN）T。图1.2显示了包含10个数据点训练集的图示 。图1.2中输入数据集x通过选择xn的值产生，其中n = 1，。 。 。 N，在范围[0，1]上均匀分布。通过计算函数sin（2πx）的对应值获得目标数据集，然后加入具有高斯分布特征的随机噪声（高斯分布在1.2.4节中讨论）到每一个这样的点来获得相应的值tn。通过这种方式产生数据，我们将捕获许多真实数据集的属性，即他们拥有的潜在规律（这是我们希望学习到的），但个别的观察被随机噪声干扰。这种噪声可能来自固有的模拟（即随机）过程，如放射性衰变，但更典型地是由于存在不可观测本身的可变性。

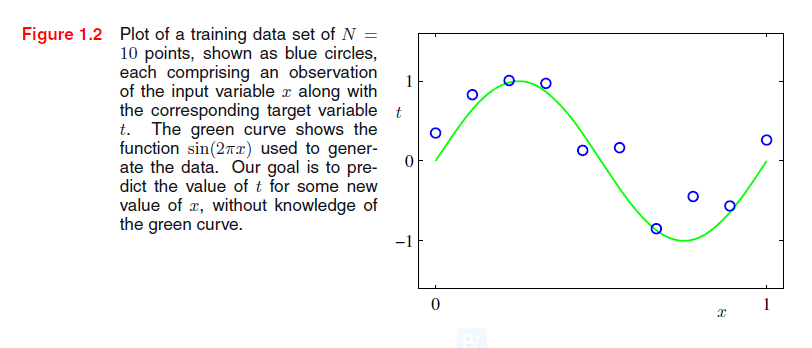
　　我们的目标是利用这个训练集，从而得到新的输入变量x对应目标变量t的预测。正如我们之后将看到的，这涉及隐含地发现潜在函数sin（2πx）。本质上这是一个困难的问题，因为我们不得不从有限的数据集中来概括。此外，观察到的数据被噪音干扰，所以对于给定的x，t的合适值有不确定性。第1.2节讨论的概率论提供了用于精确表达这种不确定性的框架和定量的方式，并且第1.5节讨论的决策论可以让我们利用此概率表示得到最优的预测。
　　然而，目前我们将非正式地开始并考虑基于曲线拟合的简单方法。特别是，我们应当用多项式函数来拟合数据

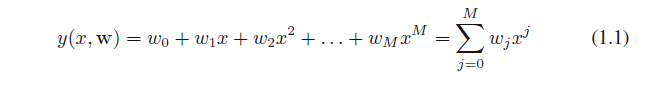
其中M是多项式的阶数，和Xj表示x的幂。多项式系数w0，， ，wm由向量w表示。注意，虽然多项式函数y（x，w）是x的非线性函数，但它是系数w的线性函数。诸如多项式这样的函数有很重要的特性并且被称为线性模型，这将在第3章和第4广泛讨论。
　　该系数的值通过拟合多项式和训练数据被确定。这可以通过最小化误差函数实现，即测量给定w函数y（x，w）的值和训练集数据点之间的失配。被广泛使用的误差函数是误差的平方和

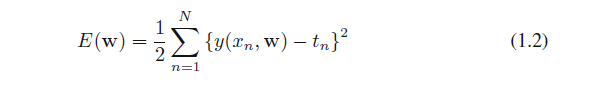
其中因子1/2是为了之后计算方便。我们将在本章后面讨论选择这个误差函数的动机。现在，我们简单地指出它是一个非负的数量，当且仅当函数y（x，w）精确地经过每个训练数据点时它是零。误差函数平方和的几何解释如图1.3。

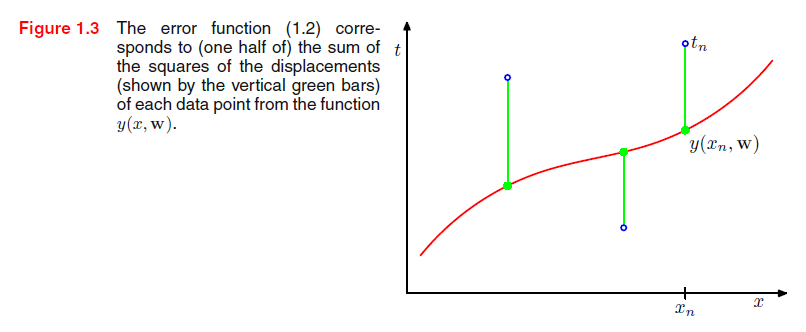
　　我们通过选择w值来解决曲线拟合问题，这个w应使E（w）尽可能小。因为误差函数是系数w的二次函数，其相对于系数的导数是线性的，因此误差函数的最小化有唯一解，用w*表示，可以在封闭的形式中找到。所得多项式由函数y（x，w）给定。
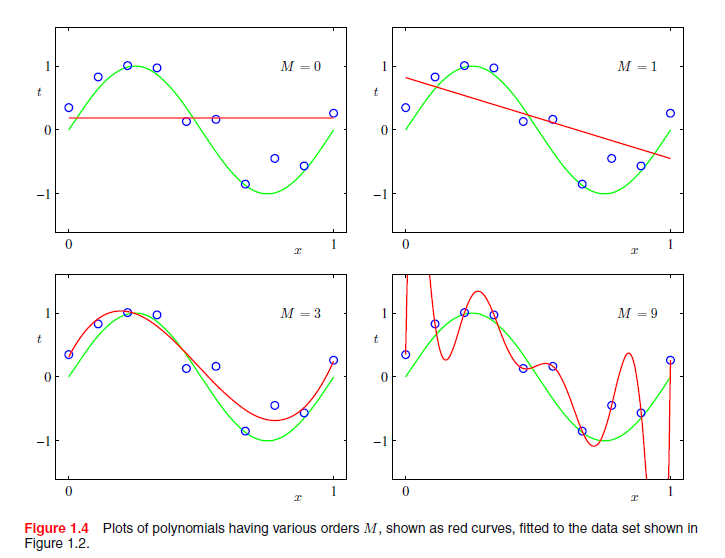
　　仍存在的问题是多项式阶数M的选择，正如我们将看到的，这将变成一个重要概念-模型比较或模型选择的例子。在图1.4中，我们显示了拟合多项式结果的四个例子，这些多项式数据集的阶数分别为M =0，1，3和9，如图1.2。
　　我们注意到，常数（M = 0）和一阶（M = 1）多项式给出比较差的数据拟合和结果函数sin（2πx）的表示也差。三阶（M=3）多项式似乎给出函数sin（2πx）最合适的拟合，如图1.4所示。当我们用更高阶多项式（M= 9），我们得到对训练数据好的拟合。事实上，多项式精确地通过每一个数据点并且E（w）=0。但是，拟合曲线振荡比较大，并给出了函数sin（2πx）比较差的表示。后一种现象被称为过拟合。

　　正如我们前面所提到的，我们的目标是通过给新数据做准确的预测来实现良好的泛化。通过考虑单独的测试集，我们可以得到一些定量的洞察到M上泛化性能的依赖，该测试集包含100个数据点，这些数据点用产生训练集点相同的过程产生。对于M的每种选择，我们可以根据式1.2评估训练数据集E（w*）的残差，我们也可以评估测试数据集的E（W）。有时使用均方根（RMS）误差更方便，其定义

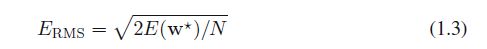
除以N允许我们咋相同的基础上比较不同大小的数据集，并且平方根确保ERMS和目标变量t在相同规模（相同的单位）上测量出来。对于不同的M值，RMS误差的训练和测试集如图1.5所示。测试集误差是衡量我们对新数据预测好坏的标准。从图1.5我们注意到较小的M值给出相对较大的测试集误差，并且这可以归因于一个事实，即相应的多项式是相当不灵活，没有能力捕捉函数sin（2πx）的震荡。范围在3和8之间的M值给出较小的测试集误差，而这些也给出了生成函数sin（2πx）的合理表示。

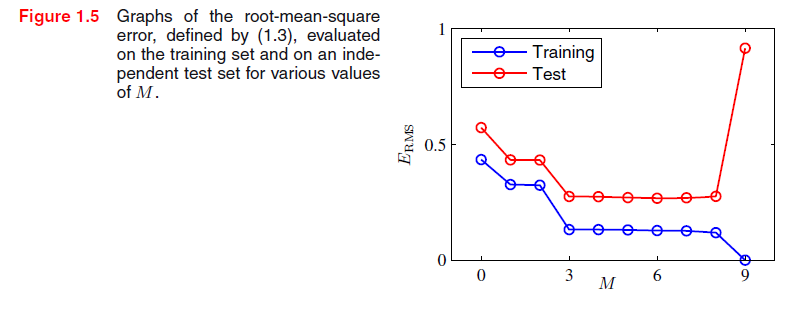
　　对于M =9，训练集误差变为零，正如我们所期望的，因为此多项式包含10个自由度对应于10个系数w0，， ，w9，所以可以准确地调整到训练集上的10个数据点。然而，测试集误差变得非常大，正如我们在图1.4中看到的，相应的函数y（x，w*）显示出了野生振荡。
　　这似乎是矛盾的，因为给定阶的多项式包含所有低阶多项式作为特殊情况。因此M=9多项式至少能够产生M=3多项式一样好的结果。此外，我们可能认为，新数据的最佳预测是函数sin（2πx）（我们将在后面看到，确实是这种情况）。我们知道，函数sin（2πx）的幂级数展开式包含所有阶，所以我们可能预计结果应该随着增加M不断提高。
　　我们通过检查从各阶多项式获得的系数w*得到一些问题的洞察，如表1.1所示。我们看到，随着m的增加，系数的大小明显地变大。特别是对于M =9的多项式，系数被细微调整到数据大的正和负值，使得相应多项式函数精确地匹配每个数据点，但数据点之间（特别是靠近区域末端）函数表现出大的振荡，从图1.4可以看出。直观上看，更灵活的多项式会逐渐调整到目标值上的随机噪声。


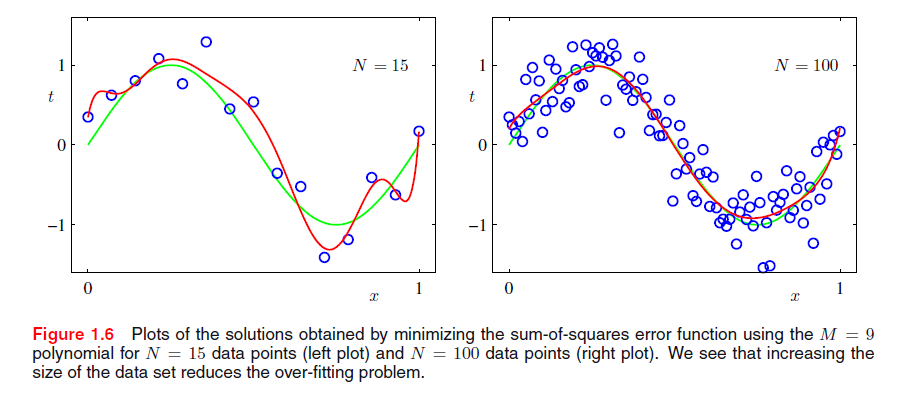
　　研究给定模型（但数据集的大小是不同的）的行为也是很有趣的，如图1.6。我们看到，对于一个给定模型的复杂性，过拟合问题随着数据集大小的增加得到了减轻。另一种说法是，数据集越大，我们提供拟合数据的模型越复杂。有时提倡的粗略启发式算法是数据点的数量应不超过自适应参数数量的某个倍数（例如5或10）。然而，正如我们将在第3章看到的，参数的数量不是最合适的模型复杂度衡量方法。
　　此外，根据现有的训练集大小限制模型参数的数量是非常不让人满意的。根据要解决问题的复杂度选择模型的复杂度似乎是更合理的。我们应当看到，寻找模型参数的最小二乘法代表最大似然的特定情况（在1.2.5节中讨论），并且过拟合问题可以理解为最大似然的一般性质。通过采用贝叶斯方法，可以避免过拟合问题。我们将看到，用贝叶斯的视角来看模型比较容易，并且该模型中参数的数目大大超过了数据点的数目。事实上，在贝叶斯模型中，有效参数数目自动适应数据集的大小。
　　然而，继续当前的方法并考虑如何将其应用到规模有限的数据集中是比较有益的。一种经常用来控制该情况下过度拟合现象的技术是正规化，这涉及添加惩罚项到误差函数（1.2）来阻止系数过大。这种惩罚项最简单的形式是所有系数的平方和，它产生一个修改的误差函数形式

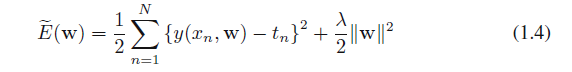
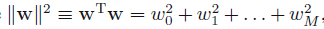
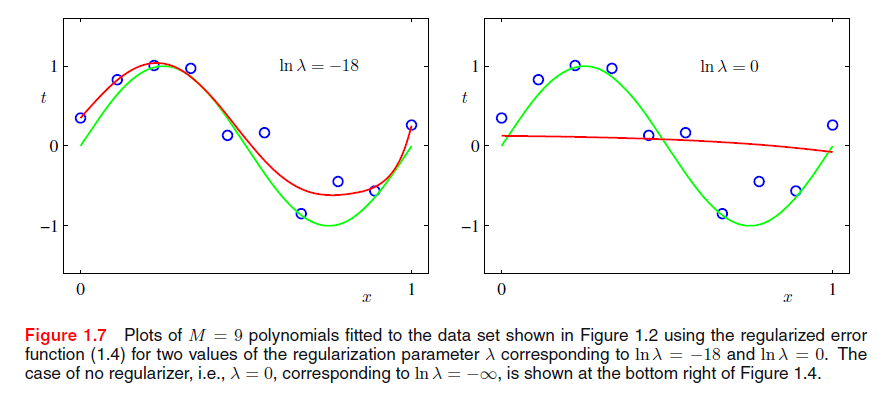
其中系数λ控制正则项相对于平方和误差的重要性。注意，常系数w0从正规化中省略，因为它的纳入导致结果依赖于目标变量原点的选择（Hastie等人，2001），或者它可能包括在内，但有它自己的正规化系数（我们将在第5.5.1节详细的讨论这个话题）。再次，误差函数可以在封闭的形式正确地被最小化。这样的技术在统计文献中叫收缩方法，因为它们减少了系数的值。二次正规化的具体情况称为岭回归（Hoerl和Kennard，1970）。在神经网络的情况下，这种方法是被誉为权值衰减。
　　图1.7显示了拟合M =9多项式的结果，数据集和之前一样但是现在使用（1.4）给出的正则化误差函数，但现在使用由（1.4）给出的正则化误差函数。我们看到，对于lnλ=-18中的一个值，过度拟合已经被抑制，我们获取潜在函数sin（2πx）更紧密的表示。然而，如果我们使用的λ值过大，那么我们又得到一个不好的拟合，如图1.7lnλ= 0。拟合多项式中对应的系数在表1.2中给出，正规化具有降低系数幅度的效果。


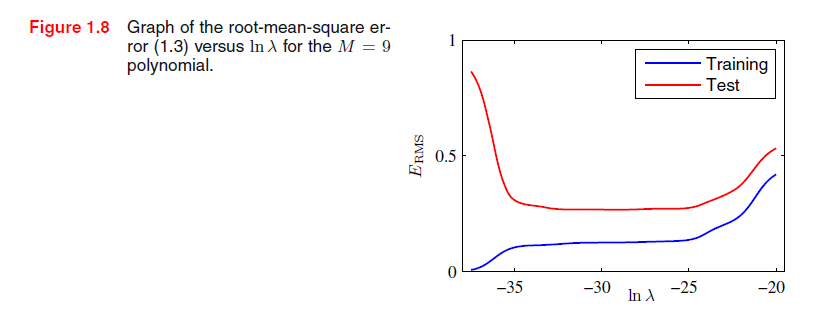
　　正则化对泛化误差的影响可以通过绘制训练数据和测试数据的RMS误差（1.3）值看出来，如图1.8。我们看到，λ的效果是控制模型有效的复杂性，因而决定了过拟合的程度。
　　模型复杂性是重要的问题，并将在1.3节讨论。这里，我们简单地指出，如果我们试图用最小误差函数做法来解决一个实际应用，那么我们将不得不找到一种方法来确定所述模型复杂性的合适的值。上述结果建议了实现这一点的简单方法，即通过取现有的数据并分割成一个训练集，曾经确定的系数w和一个单独的验证集，也称为hold-out集，用于优化模型的复杂性（M或λ）。然而在很多情况下这将被证明是太浪费宝贵的训练数据，我们必须寻求更先进的方法。
　　到目前为止，我们对多项式曲线拟合的讨论主要来自于直觉。现在，我们通过转向概率论的讨论寻求更原则性的方法来解决模式识别里的问题。它对本书中几乎所有的后续发展提供了基础，也将给我们一些多项式曲线拟合中重要概念的见解，并允许我们延伸这些到更复杂的的情况。