PRML-系列二之2.3

高斯分布

高斯，也称为正态分布，在连续变量分布中是被广泛使用的模型。在单一变量x的情况下，高斯分布可以写成如下形式

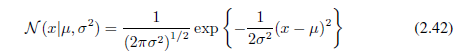
其中μ是均值，σ2是方差。对一个D维向量x，多元高斯分布的形式为

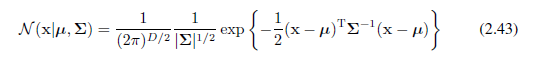
其中μ是一个D维均值向量，Σ是DxD的协方差矩阵，并且|Σ|表示Σ的行列式。
高斯分布出现在许多不同的环境中和可以从各种不同的角度激发出来。例如，我们已经看到对于单一实变量，最大化熵的分布是高斯分布。这个属性也适用于多元高斯。
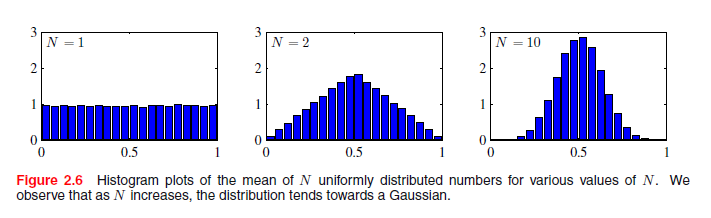
高斯分布出现的另一种情况是考虑多个随机变量之和。中心极限定理（由于拉普拉斯）告诉我们，在一定的条件下，一组随机变量的和（当然他们本身就是一个随机变量）具有这样的分布，随着项数的增加分布越来越接近高斯分布（Walker，1969）。我们考虑N个变量x1，， ，xn，每个都是区间[0，1]上的均匀分布，然后考虑平均值（x1 +···+ xn）/ N的分布。对于较大的N，这种分布趋于高斯分布，如图2.6。在实践中，随着N的增加收敛到高斯是非常迅速的。这一结果的后果是，二项式分（2.9），当N→∞（见图2.1N = 10）时趋向于高斯分布。

高斯分布有很多重要的分析属性，我们将考虑其中的几个细节。该部分是比之前的部分设计更多的技术，并且要求熟悉附录C中各种矩阵恒等式。但是，我们强烈鼓励读者熟练地使用这里的方法来处理高斯分布，因为这对于理解后面更复杂的模型是非常有帮助的。
我们首先考虑高斯分布的几何形式。x上高斯分布的函数依赖是二次形的：

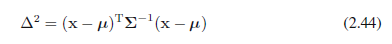
Δ是从μ到x的马氏距离，并且当Σ是单位矩阵时它就降为欧氏距离。高斯分布在x空间的表面是常数，其中这个二次形是常数。
首先，因为任何反对称成分将从指数中消失，所以不失一般性，矩阵Σ是对称的。现在考虑协方差矩阵的特征向量方程

其中i=1，，，D。因为Σ是实数，对称矩阵，它的特征值将是实数，并且它的特征向量可以形成一个标准正交集，以便

其中，Iij是单位矩阵的i，j元素，且满足

协方差矩阵Σ可以表示为其特征向量形式的扩展

类似的逆协方差矩阵Σ-1可以表示为

将（2.49）代入到（2.44），二次形变为

我们已经定义了

我们可以将{yi}解释为相对于原始xi坐标平移旋转得到的正交矢量ui定义的新坐标系。形成了向量y=（y1，…，yD）T，我们有

其中U的行是uTi。从（2.46）可以得出U是正交矩阵，即它满足UUT= I，因此也UTU= I，其中I是单位矩阵。
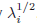
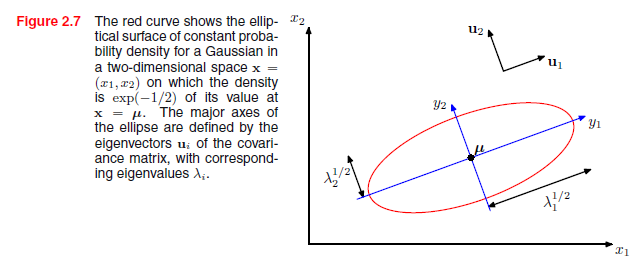
二次形和高斯密度在表面上是常数，其中（2.51）是常数。如果所有特征值λi都是正的，那么这些表面表示椭球，他们的中心在μ，他们的轴沿着ui方向，并且轴方向的比例因子是，如图2.7。

对于很好的定义高斯分布，有必要对协方差矩阵的所有特征值λI要求为正，否则分布不能正确地归一化。特征值严格为正的矩阵叫做正定的。在第12章中，我们还会遇到高斯分布中特征值中一个或多个为零的情况，在这种情况下分布奇异的并被限制在较低维数的子空间。如果所有的特征值非负，则协方差矩阵被认为是半正定。
现在考虑由yi定义的新坐标系中的高斯分布形式。从x到y坐标系，我们有一个雅可比矩阵J且给定元素

其中，Uji是矩阵UT的元素。使用矩阵U的正交性，我们看到雅可比矩阵行列式的平方是

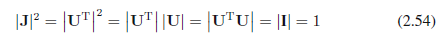
因此|J|=1。另外，协方差矩阵的行列式|Σ|可写作其特征值的乘积，因此

因此，在yj坐标系中，高斯分布的形式为

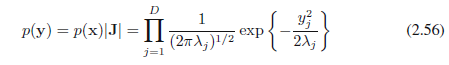
这是D个独立单变量高斯分布的乘积。特征向量定义了平移和旋转坐标的新集。 y坐标系统中的分布积分是

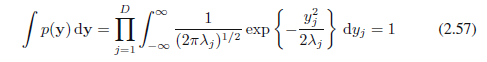
在这里，我们使用结果（1.48）用于单变量高斯的归一化。这证实了多元高斯（2.43）确实被归一化了。
我们现在看一下高斯分布，提供参数μ和Σ的解释。 高斯分布中x的期望由下式给出

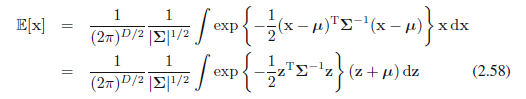
其中用z=x-μ来改变变量。我们现在注意到，指数是z分量的偶函数，因为积分区间是（-∞，∞），（z+μ）项因为对称将消失。从而

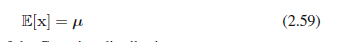
因此我们用μ作为高斯分布的均值。
我们现在考虑高斯的二阶矩。在单变量的情况下，我们认为E[x2]给出二阶矩。对于多元高斯，E[xixj]给出D2个二阶矩，我们可以将他们组在一起形成矩阵E[xxT]。此矩阵可以写成

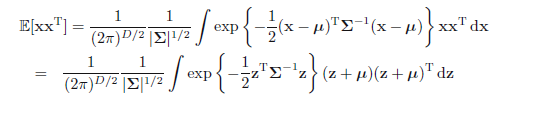
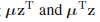
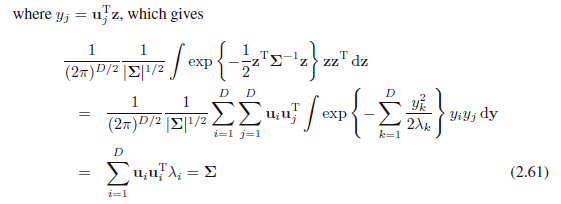
其中，我们再次使用z=x- μ来改变变量。注意，涉及的交叉项将再次因为对称性消失。μμT是常数并且可以被移到积分外，因为高斯分布归一化它本身是一个整体。考虑涉及zzT的项，我们可以使用（2.45）给出的协方差矩阵的特征向量扩展，以及特征向量的完整性得出


这里我们用特征向量式（2.45），加上中间行右手侧上的积分通过对称消失（除非i= j）。最后一行，我们利用结果（1.50）和（2.55），连同（2.48）。因此，我们有

对于单随机变量，我们取二阶矩之前减去均值以便定义方差。同样地，在多变量情况下，减去均值也是方便的，它产生一个随机向量x的协方差，该随机变量x定义为

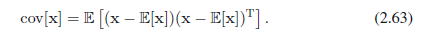
对于高斯分布的特定情况，我们可以利用E[x]=μ，及结果（2.62）得到

由于参数矩阵Σ控制x的协方差，所以它被称为协方差矩阵。
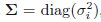
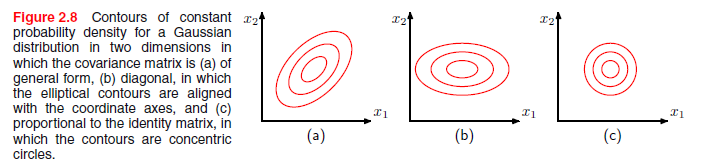
虽然高斯分布（2.43）被广泛地用作密度模型，但它存在一些显著的局限性。考虑分布中自由参数的数目，一般对称协方差矩阵Σ将有D（D + 1）/ 2个独立参数，在μ中有D个独立参数，一共给出D（D + 3）/ 2个参数。对于较大的D，参数的总数是以D平方的方式增长，操作和求逆大型矩阵的计算任务令人望而却步。解决这个问题的一个方法是使用协方差矩阵的限制形式。如果我们考虑的协方差矩阵是对角的，使得，然后我们有2D个独立参数。常数密度对应的轮廓由轴对齐的椭圆给出。我们可以进一步限制协方差矩阵与单位矩阵成比例，Σ=σ2I称为各向同性协方差，给出D + 1个独立参数。一般情况，对角和各向同性协方差的三种可能矩阵示于图2.8。不幸的是，这样的方法限制分布中自由度的数目和使协方差矩阵的求逆更快，他们也极大地限制了概率密度形式并限制其捕捉数据中相互关系的能力。

高斯分布的另一个限制是，它本质上是单峰（即有一个最大值），因此不能对多峰分布提供良好的近似。因此，高斯分布既可以是灵活的（具有许多参数的情况），同时对分布的范围有太多限制。后面我们会看到，引进潜变量，也称为隐变量或不可观测变量，两个问题都可以解决。特别地，多峰分布族是通过引入离散潜变量（导致了高斯混合）得到的，如第2.3.9讨论的。同样，不断引进潜变量，如第12章，导致模型中自由参数的数目由数据空间的维数D独立控制，同时允许该模型捕捉数据集中主要的关系。实际上，这两种方法可以结合起来，并进一步延伸导出一套分层模型，从而能适应广泛的实际应用。例如，马尔可夫随机场的高斯版本（它被广泛地用作图像的概率模型）是像素强度联合空间上的高斯分布，但通过考虑反应像素空间组织的结构该问题变得容易处理。同样，线性动态系统用于建模时间序列数据（一些应用例如跟踪），也是潜在的大量观察数据和潜在变量的联合高斯分布，并且由于该结构也变得非常容易处理。表达复杂分布形式和性质的一个强有力框架是概率图模型，这将是
第8章的主题。