漫步微积分十二——隐函数、分数指数

目前我们遇到的大部分函数形式都是$y=f(x)$，$y$直接或明确的表示成$x$的形式。然而，我们常常看到如下形式的定义

$$\begin{equation} F(x,y)=0\tag1 \end{equation}$$

不仅仅牵涉到$y$，$x,y$他们互相或多或少有点牵连。当给定一个$x$值，等式通常对应一个或多个$y$值。对这种情况，我们称$y$是$x$的隐函数。

例1：(a)考虑一个简单的等式，$xy=1$，它确定了一个$x$的隐函数，我们可以显示的写为

$$y=\frac{1}{x}$$

(b)等式$x^2+y^2=25$确定了两个$x$的隐函数，显示的表达为

$$y=\sqrt{25-x^2}\qquad y=-\sqrt{25-x^2}.$$

我们都知道，这两个函数图像分别是半径为5的圆的上下两部
分，如图1。

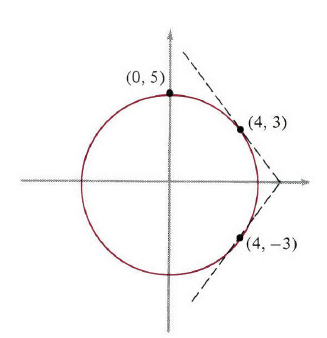
图1

(c)等式$2x^2-2xy=5-y^2$也确定了两个隐函数。如果看作$y$ 的二次函数，那么函数解为

$$y=x+\sqrt{5-x^2}\quad y=x-\sqrt{5-x^2}$$

(d)等式$^3+y^3=3axy(a>0)$确定了几个隐函数，但是解决它比较麻烦，所以跳过它吧(嘿嘿嘿)。

我们经常会遇到需要计算隐函数的导数$\frac{dy}{dx}$但开始却没有$y$等式的情况。根据链式法则，等式两边直接对$x$ 求导,无论$y$在哪里出现，都将其看作$x$的函数。例如，$y^3$看作$x$函数的立方，它的导数为

$$\frac{d}{dx}y^3=3y^2\frac{dy}{dx}$$

$x^3y^4$看作两个$x$函数相乘，其导数为

$$\frac{d}{dx}(x^3y^4)=x^3\cdot 4y^3\frac{dy}{dx}+y^4\cdot 3x^2$$

为了完成整个过程，将$dy/dx$代入即可。这个方法叫做隐函数求导。我们将它应用到例1，展示了它的工作过程。

例2：(a)我们把等式$xy=1$看作两个相等的$x$函数(即：$xy$和1)。这两个函数的导数是相等的，所以

$$x\frac{dy}{dx}+y=0\quad or \quad \frac{dy}{dx}=-\frac{y}{x}$$

根据原等式可以求出$y=1/x$，代入的

$$\frac{dy}{dx}=-\frac{y}{x}=-\frac{1}{x}\cdot\frac{1}{x}=-\frac{1}{x^2}$$

对$y=1/x$直接求导得

$$\frac{dy}{dx}=-\frac{1}{x^2}$$

(b)对等式$x^2+y^2=25$进行求导得

$$2x+2y\frac{dy}{dx}=0\quad or\quad \frac{dy}{dx}=-\frac{x}{y}$$

无论对那个隐函数，它都给出了正确的结果。图1中点(4,3)位于上半部分，$dy/dx$是$-\frac{4}{3}$，点(4,-3)位于下半部分，$dy/dx$是$\frac{4}{3}$

(c)对等式$2x^2-2xy=5-y^2$隐式求导得

$$4x-2x\frac{dy}{dx}-2y=-2y\frac{dy}{dx}\quad or\quad \frac{dy}{dx}=\frac{2x-y}{x-y}.$$

(d)在例1(d)中，$dy/dx$的导数无法直接计算。然而，利用隐函数将会容易许多。对$x^3+y^3=3axy$，我们有

$$3x^2+3y\frac{dy}{dx}=3ax\frac{dy}{dx}+3ay\quad or \quad \frac{dy}{dx}=\frac{ay-x^2}{y^2-ax}$$

很明显，隐函数求导通常给出$dy/dx$的形式，包含了$x,y$而不是只有$x$。但是，在许多情况下这并非是个缺点。例如，如果我们计算一个等式在点$(x_0,y_0)$处切线的斜率，我们需要做的就是将$x_0,y_0$代入公式$dy/dx$。 例2(b)在点(4,3)和(4,-3)的情况就说明了这一点。

现在我们利用隐函数求导来说明下面的公式对所有分数指数$n=p/q$依然成立

$$\begin{equation} \frac{d}{dx}x^n=nx^{n-1}\tag2 \end{equation}$$

为了方便，我们对(2)式引入一个因变量

$$y=x^{p/q}$$

两边都去$q$次方的

$$y^q=x^p$$

两边对$x$求导并利用整数的幂规则得

$$qy^{q-1}\frac{dy}{dx}=px^{p-1}$$

或者

$$\frac{dy}{dx}=\frac{p}{q}\frac{x^{p-1}}{y^{q-1}}$$

而$y^{q-1}=y^q/y=x^p/x^{p/q}$，所以

$$\frac{dy}{dx}=\frac{p}{q}\frac{x^{p-1}}{y^{q-1}}=\frac{p}{q}\frac{x^{p-1}}{x^p}\cdot x^{p/q}=\frac{p}{q}x^{p/q-1}$$

得证。

例3：根据上面的结论，我们立马可以得出

$$\frac{d}{dx}x^{1/2}=\frac{1}{2}x^{-1/2},\quad \frac{d}{dx}x^{-2/3}=-\frac{2}{3}x^{-5/3},\quad \frac{d}{dx}x^{5/4}=\frac{5}{4}x^{1/4}$$

第一个经常写成如下形式

$$\frac{d}{dx}\sqrt{x}=\frac{1}{2\sqrt{x}}$$

例4：对于有基底的表达式求导，首先用分数来替换所有基底。

$$\begin{eqnarray*} \frac{d}{dx}\frac{x}{\sqrt{x^2-1}} &=&\frac{d}{dx}x(x^2-1)^{-1/2}=x\left(-\frac{1}{2}\right)(x^2-1)^{-3/2}(2x)+(x^2-1)^{-1/2}\\ &=&\frac{-x^2}{(x^2-1)^{3/2}}+\frac{1}{(x^2-1)^{1/2}}=\frac{-x^2+(x^2-1)}{(x^2-1)^{3/2}}=-\frac{1}{(x^2-1)^{3/2}} \end{eqnarray*}$$

目前为止提到的所有规则将被用于许多方面。因此，最好能够记住他们，并多加练习达到能立马写出的地步。一位哲学家曾说过：文明进步依赖于不加思索就能够说出的运算数量。

有一点值得说明，在计算导数时，幂规则和除法法则最容易出错。例如，对于幂规则，很容易忘记$du/dx$。而除法法则易错点是分子里减法的顺序。如果忘记的话，我们可以利用乘法法则迅速推导出来：

$$\begin{eqnarray*} \frac{d}{dx}\left(\frac{u}{v}\right) &=&\frac{d}{dx}(uv^{-1})=u\cdot (-1)v^{-2}\frac{dv}{dx}+v^{-1}\frac{du}{dx}\\ &=&\frac{1}{v}\frac{du}{dx}-\frac{u}{v^2}\frac{dv}{dx}=\frac{vdu/dx-udv/dx}{v^2} \end{eqnarray*}$$

{\color{red}{注解}}$\quad$例1(d)有一段很长的历史，值得进一步评论一下。它的图像叫做笛卡尔叶，如图2。考虑最简单的情况即$a=1$，那么等式变为

$$\begin{equation} x^3+y^3=3xy\tag3 \end{equation}$$

用$x$的形式表示$y$求不出解。因此有许多历史爱好者的故事。

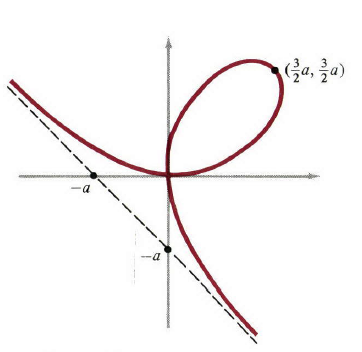
图2

1545年，意大利医生家、数学家、占星家吉罗拉莫 卡尔达诺(1501-1576)用基的方法发现了任何三次方程解的公式。这个公式类似于大家熟悉的二次公式但是要复杂得多。如果用卡尔达诺的公式求解方程(3)，那么有三个解函数
$$y_1=\sqrt[3]{-\frac{x^3}{2}+\sqrt{\frac{x^6}{4}-x^3}}+\sqrt[3]{-\frac{x^3}{2}-\sqrt{\frac{x^6}{4}-x^3}}$$

和

$$y_2,y_3=-\frac{1}{2}y_1\pm \frac{1}{2}\sqrt{-3}\left(\sqrt[3]{-\frac{x^3}{2}+\sqrt{\frac{x^6}{4}-x^3}}-\sqrt[3]{-\frac{x^3}{2}-\sqrt{\frac{x^6}{4}-x^3}}\right)$$

隐函数求导的方法明显比这样直接求导好许多。再说，对于下面的等式

$$x^5+5x^4y^2+3xy^3+y^5=1$$

无法用$x$的形式来表示$y$，但是利用隐函数求导法则可以很容易的得到导数。