漫步线性代数九——求Ax=0和Ax=b

前面的文章关注的是方阵的逆矩阵，$Ax=b$有一个解的话它就是$x=A^{-1}b$，它可以通过消元法得到。一个长方形矩阵带来的新的可能性——$U$可能没有所有的主元，本文我们就将$U$ 化为形式$R$—— 消元法能给出的最简矩阵，$R$立马给出所有解。

对于一个可逆矩阵，零空间只包含$x=0$，列空间就是整个空间，当零空间不仅仅包含零向量而(或)列空间没有包含所有向量时新的问题出现了：

1. 零空间里的任意向量$x_n$可以加到一个特解$x_p$ 上，所有线性方程解的形式为$x=x_p+x_n$：
   $$Ax_p=b\quad Ax_n=0\text{得到}A(x_p+x_n)=b$$
2. 当列空间不包含$R^m$里的所有$b$时，我们需要对$b$添加限制使得$Ax=b$有解。

接下来我们举一个$3\times 4$的例子，将计算$Ax=0$ 的所有解，找出$b$位于列空间(这样的话$Ax=b$就是可解的)的条件。首先考虑一个最简单的，对于$1\times 1$ 系统的$0x=b$，一个方程和一个未知量有两种可能：

1. $0x=b$除了$b=0$外无解，$1\times 1$矩阵的列空间只包含$b=0$。
2. $0x=0$有无限多个解，零空间包含所有的$x$，一个个特解是$x_p=0$，完整解是$x=x_p+x_n=x+(any\ x)$

同样的现在开始考虑$2\times 2$的例子，对于第一行为1，第二行为2的矩阵是不可逆的：$y+z=b_1,2y+2z=b_2$通常没有解。

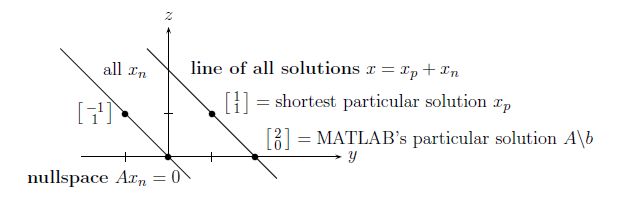
图1

除了$b_2=2b_1$外没有其他解，$A$的列空间只包含两元素比值为2的$b$；当$b_2=2b_1$时，有无限多个解，$y+z=2,2y+2z=4$的特解是$x_p=(1,1)$，图1中$A$的零空间包含$(-1,1)$以及它的倍数$x_n=(-c,c)$：

$$\begin{matrix} y&+&z&=&2\\2y&+&2z&=&4 \end{matrix}\quad \text{完整解为}\quad x_p+x_n= \begin{bmatrix} 1\\1 \end{bmatrix} + c \begin{bmatrix} -1\\1 \end{bmatrix}= \begin{bmatrix} 1-c\\1+c \end{bmatrix}$$

梯度形U和行最简形R

我们从$3\times 4$矩阵开始，首先得到$U$进步一得到$R$：

$$A=\begin{bmatrix} 1&3&3&2\\2&6&9&7\\-1&-3&3&4 \end{bmatrix}$$

主元$a_{11}=1$非零，通常的初等变换将使这个主元下面的元素变为零，而坏消息出现在第二列：

$$A\to\begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&6&6 \end{bmatrix}$$

第二个候选主元是零：我们不接受这种主元。我们试图找出它下面是否存在非零元素，从而通过交换即可，不幸的是下面都是零。如果$A$是方阵，那么这个信号告诉我们矩阵时奇异的，而对于长方形矩阵，还没有结束，接下来我们能做的就是继续看下一列，发现主元是3，从第三行减去第二行的两倍就得到了$U$：

$$U=\begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&0&0 \end{bmatrix}$$

严格来讲，我们接下来该处理第四列，因为第三个主元位置是零所以就不需要的。$U$是上三角矩阵但是它的主元不在对角线上，$U$的非零元素类似于阶梯形状，如图2$5\times 8$所示，星号表示的元素可能为零也可能不是零。

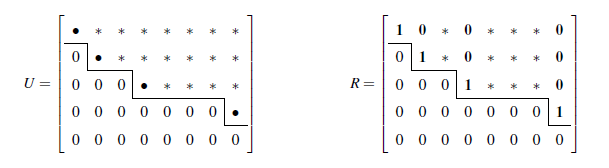
图2

对任何矩阵我们都可以得到这种阶梯形式$U$：

1. 主元是每行第一个非零元素。
2. 每个主元所在列的下面都是零。
3. 每行的主元位于上面那行主元的右边，这样产生阶梯形式并且零行在最后。

因为我们从$A$开始，到$U$结束，大家可能会问：这和之前的$A=LU$一样吗？答案是肯定的，因为消元步骤没有变，每一步都是下面一行减去上面行的倍数，每一步的逆都是加上所减行的倍数，这些逆操作以正确的方式组合到一起直接到的$L$：

$$L=\begin{bmatrix} 1&0&0\\2&1&0\\-1&2&1 \end{bmatrix} \quad and\quad A=LU$$

注意$L$是方阵，它和$A,U$有相同的行数。

一般情况下都需要置换操作，而我们的例子不需要用置换矩阵$P$进行行变换，因为当主元不存在时，我们就进入下一列，不需要假设$A$是非奇异的：

2、对于任意$m\times n$矩阵$A$，存在一个置换矩阵$P$，单位下三角矩阵$L$和$m\times n$阶梯型矩阵$U$，使得$PA=LU$。

现在我们比$U$更深入一点讨论行最简形$R$，使矩阵更简单。第二行的除以3使得所有主元为1，然后令主元的上面都为零，这一次我们我们从上面的行减去下面行的倍数，那么最终的结果就是最简行阶梯行矩阵$R$：

$$\begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&0&0 \end{bmatrix} \to \begin{bmatrix} 1&3&3&2\\0&0&1&1\\0&0&0&0 \end{bmatrix} \to \begin{bmatrix} 1&3&0&-1\\0&0&1&1\\0&0&0&0 \end{bmatrix} =R$$

矩阵$R$是$A$消元得到的最终结果。

那么可逆方阵的行最简阶梯型是什么样的呢？答案是单位矩阵。他们有完整的主元集合且都为1，主元上下又都为零，所以$A$可逆的情况下为单位矩阵。

对于$5\times 8$矩阵，图2给出了行最简形式$R$，四个主元所在的行和列组成了一个单位矩阵，从$R$中我们可以迅速找出$A$的零空间，$Rx=0$和$Ux=0,Ax=0$ 有相同解。

主元变量和自由变量

我们的目标是求出$Rx=0$的所有解，主元是至关重要的：

$$Rx=\begin{bmatrix} 1&3&0&-1\\0&0&1&1\\0&0&0&0 \end{bmatrix} \begin{bmatrix} u\\v\\w\\y \end{bmatrix}= \begin{bmatrix} 0\\0\\0 \end{bmatrix}$$

未知量$u,v,w,y$分成了两组，一组包含主元变量，他们对应主元所在的列，第一和第三列包含主元，所以$u,w$是主元变量；另一组组成自由变量，对应于没有主元的列，他们是第二和第四列，所以$v,y$是自由变量。

为了求出$Rx=0$的通解，我们可能给自由变量分配任意值，假设我们已经分配了$v,y$值，那么主元变量就完全可以用$v,y$ 的形式确定：

$$\begin{equation} Rx=0 \quad \begin{matrix} u&+&3v&-&y&=&0\\&&w&+&y&=&0 \end{matrix}\quad \text{得到}\quad \begin{matrix} u&=&-3v&+&y\\w&=&&-&y \end{matrix}\tag1 \end{equation}$$

完整解可以表示成这两个特殊解的组合：

$$\begin{equation} x=\begin{bmatrix} -3v+y\\v\\-y\\y \end{bmatrix}= v\begin{bmatrix} -3\\1\\0\\0 \end{bmatrix} +y \begin{bmatrix} 1\\0\\-1\\1 \end{bmatrix}\tag2 \end{equation}$$

再次观察一下这个完整结，特殊解$(-3,1,0,0)$有两个自由变量$v=1,y=0$，另一个特解$(1,0,-1,1)$为$v=0,y=1$。所有解是这两个解的线性组合，求$Ax=0$ 解的最好方式是找出特解：

1. 化简为$Rx=0$后，确定主元变量和自由变量
2. 将一个自由变量设置为1，另一个设置为0求$Rx=0$，得到的$x$是一个特解
3. 第二步中每一个自由变量都会得到它对应的特解，这些特解的组合形成了零空间也就是$Ax=0$的所有解。

在向量$x$所在的四维空间里，$Ax=0$的解形成一个二维子空间也就是$A$的零空间。例如，$N(A)$由向量$(-3,1,0,0),(1,0,-1,1)$产生，他们的组合得到整个子空间。

这里有一个小技巧，使得从$R$中求特解很容易。3,0，-1和1 在$R$的非主元列，改变他们的符号找出特解中的主元。我们将方程(2)的特解放到矩阵矩阵$N$中，这样就能看出这个想法了：

$$N= \begin{bmatrix} -3&1\\1&0\\0&-1\\0&1 \end{bmatrix}$$

自由变量是1和0，当自由变量移到方程(2)的右边时，他们的系数3,0，-1和1改变了符号，他们确定了特解中的主元变量。

这里给出一个重要的理论。假设矩阵列数比行数大$n>m$，因为$m$行最多有$m$ 个主元，所以至少存在$n-m$个自由变量，如果$R$的某些行是零，那么会有更多的自由变量；但是不管怎样，只有有一个是自由变量，这个自由变量可以分配任意值，由它得出下面的结论：

3、如果$Ax=0$未知量比方程多，那么它至少有一个特解：除了平凡解$x=0$外至少还有一个解。

肯定有无限多个解，因为任何常数$c$都能满足$A(cx)=0$，零空间包含通过$x$ 的直线，如果有额外的自由变量，那么零空间就不仅仅是$n$维空间的一条线，零空间的维数和自由变量，特解的数目是一样的。

中心思想(子空间的维数)在下一篇文章里会精确给出，为了零空间我们处理自由变量，为了列空间我们处理变量。

解Ax=b,Ux=c,Rx=d

$b\neq0$的情况不同于$b=0$，$A$上的行运算也必须在右边$b$上执行，我们先用字母$(b_1,b_2,b_3)$找出可解的条件，然后令$b=(1,5,5)$找出所有解。

对于最开始的例子，我们令$Ax=b=(b_1,b_2,b_3)$，两边都进行行运算得：

$$\begin{equation} Ux=c\quad \begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&0& \end{bmatrix} \begin{bmatrix} u\\v\\w\\y \end{bmatrix}= \begin{bmatrix} b_1\\b_2-2b_1\\b_3-2b_2+5b_1 \end{bmatrix}\tag3 \end{equation}$$

右边执行完前向消去后得到向量$c$。

对等式是否有解还不是很清楚，第三个等式比较麻烦，因为它的左边是零，除非右边$b_3-2b_2+5b_1=0$，否则方程就不一致。即便未知数的个数比方程多，但依然有可能无解。我们知道如果$b$位于$A$的列空间，那么$Ax=b$就有解，子空间来自$A$的四个列：

$$\begin{bmatrix} 1\\2\\-1 \end{bmatrix} , \begin{bmatrix} 3\\6\\-3 \end{bmatrix} , \begin{bmatrix} 3\\9\\3 \end{bmatrix} , \begin{bmatrix} 2\\7\\4 \end{bmatrix}$$

虽然是四个向量，但是他们的组合只是三维空间中的一个平面，列2 是列1的三倍，第四列等于第三列减去第一列，这些相互依赖列如第二和第四列是没有主元的。

列空间$C(A)$可以用两种方式来描述，一方面，它是列1和3产生的平面，其他位于该平面的列不会得出新的列。等价的，它是满足$(b_3-2b_2+5b_1=0$的所有向量$b$组成的平面；如果系统是可解的，这就是约束条件。几何上我们会看到$(5,-2,1)$垂直于每个列。

如果$b$属于列空间，$Ax=b$的解很容易找到，$Ux=c$的最后一个方程是$0=0$。对于自由变量$v,y$，我们可以像以前一样分配任意值，主元变量$u,v$依然通过回代确定。对于$b_3-2b_2+5b_1=0$这个特例，选择$b=(1,5,5)$：

$$Ax=b\quad \begin{bmatrix} 1&3&3&2\\2&6&9&7\\-1&-3&3&4 \end{bmatrix} \begin{bmatrix} u\\v\\w\\y \end{bmatrix}= \begin{bmatrix} 1\\5\\5 \end{bmatrix}$$

前向消元在左边得到$U$，右边得到$c$：

$$Ux=c\quad \begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&0&0 \end{bmatrix} \begin{bmatrix} u\\v\\w\\y \end{bmatrix}= \begin{bmatrix} 1\\3\\0 \end{bmatrix}$$

最后一个方程$0=0$，然后回代：

$$\begin{matrix} &&&&3w&+&3y&=&3\\u&+&3v&+&3w&+&2y&=&1 \end{matrix} \qquad \begin{matrix} w&=&1&-&y\\u&=&-2&-&3v&+y \end{matrix}$$

$v,y$是自由变量：

$$\begin{equation} x=\begin{bmatrix} u\\v\\w\\y \end{bmatrix} =\begin{bmatrix} -2\\0\\1\\0 \end{bmatrix} +v\begin{bmatrix} -3\\1\\0\\0 \end{bmatrix} +y\begin{bmatrix} 1\\0\\-1\\1 \end{bmatrix}\tag4 \end{equation}$$

后两项可得出许多解，$Ax=b$的每个解是特解和$Ax=0$解的和，方程(4)的特解通过将所有主元变量设为零得到。

几何上，这个解依然是一个二维平面，但是不是子空间，因为它不包含$x=0$，它平行于我们之前得到的子空间。现在列出求解步骤：

1. 将$Ax=b$化为$Ux=c$
2. 将自由变量设为0，求出$Ax_p=0,Ux_p=c$的一个特解。
3. 求出$Ax=0(Ux=0\ or\ Rx=0)$的解，对每一个自由变量轮流等于1即可，那么$x=x_p+x_n$

当方程是$Ax=0$时，特解是零向量！它满足上面的模式，但是$x_p=0$没有在(2)中写出来。

问题：化简形式$R$如何让解更加清楚？从我们的例子中可以看出，方程1减去方程2然后方程2除以它的主元。左边得到$R$，右边$(1,3,0)$变成$(-2,1,0)$：

$$\begin{equation} \begin{bmatrix} 1&3&0&-1\\0&0&1&1\\0&0&0&0 \end{bmatrix} \begin{bmatrix} u\\v\\w\\y \end{bmatrix} =\begin{bmatrix} -2\\1\\0 \end{bmatrix}\tag5 \end{equation}$$

我们的特解$x_p$的自由变量为$v=y=0$，忽略掉2和4列，所以立马得到$u=-2,w=1$。

现在我们总结一下，消元揭示了主元变量和自由变量，如果有$r$个主元，那么就有$r$个主元变量和$n-r$个自由变量，这个重要的数字$r$有一个重要的名字——矩阵的秩。

4、假设消元$Ax=b$得到$Ux=c,Rx=d$，有$r$个主元行和$r$ 个主元列。这些矩阵的秩是$r$，$U,R$的最后$m-r$是零，所以如果$c,d$的最后$m-r$个元素也是零的话就存在解。

完整解是$x_p+x_n$，一个是所有自由变量为零得特解$x_p$，它的主元变量是$d$的$r$个元素，所以$Rx_p$=d。

零空间解$x_n$是$n-r$个解的组合，每一个自由变量为1。解中的主元变量可以在$R$中对应的列中找到(符号相反)。

我们可以看出秩$r$非常重要，它是行空间中主元行的数目，也是列空间中主元列的数目，零空间中有$n-r$个解，对$b,c,d$有$m-r$个可解条件。