漫步线性代数十三——线性变换

我们已经知道了矩阵$A$的四个基本空间，它的零空间使得向量变成零向量，因为$Ax$是列的组合，所以所有向量都位于列空间里。之后我们还会看到一些每秒的东西——$A$将它的行空间变成列空间，在这些维度为$r$的空间上矩阵是可逆的，这是矩阵$A$的实际操作，还有一部分被零空间和左零空间隐藏了。

假设$x$是一个$n$为向量，当$A$乘以$x$的时候，它将向量变成了一个新的向量$Ax$，对于$R^n$空间里的所有点$x$都会发生这种变化，整个空间被矩阵$A$变换了，图1给出了矩阵的四种变换：

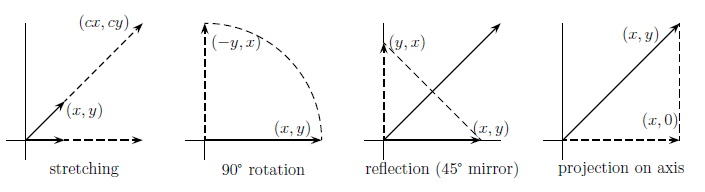
图1：四种矩阵的变换

1、$A=\begin{bmatrix}c&0\\0&c\end{bmatrix}$，它是单位矩阵乘以常数得到的，$A=cI$，将每个向量拉伸$c$倍，整个空间被拉长或收缩。

2、$A=\begin{bmatrix}0&-1\\1&0\end{bmatrix}$，旋转矩阵，它将空间绕原点进行旋转，图中的例子是旋转了90度，每个点从$(x,y)$变成$(-y,x)$。

3、$A=\begin{bmatrix}0&1\\1&c\end{bmatrix}$，反射矩阵，它将每个向量做关于某个镜面的反射，图中的镜面是直线$y=x$，像$(2,2)$这类点不会发生变化，像$(2,-2)$这类点翻转成$(-2,2)$。像$v=(2,2)+(2,-2)=(4,0)$这类点一部分变化一部分不变，$Av=(2,2)+(-2,2)=(0,4)$。

反射矩阵也是置换矩阵！在代数上它非常简单，就是将$(x,y)$变成$(y,x)$，而在几何图像上被掩盖了。

4、$A=\begin{bmatrix}1&0\\0&0\end{bmatrix}$，投影矩阵，它将整个空间投影到低维子空间上(不可逆)，图中是将平面的每个向量$(x,y)$变为水平轴上最近的点$(x,0)$。这个轴是$A$ 的列空间，投影为$(0,0)$的$y$轴是零空间。

这些例子也可以放到三维空间里，此时矩阵将是在空间中进行缩放，沿着平面旋转或反射，将一切事物投影到二维平面上。另外知道矩阵不能做什么也是很重要，某些变化$T(x)$利用$Ax$就做不到：

• 不可能移动原点，因为对于每个矩阵$A0=0$。
• 如果向量$x$变成$x'$，那么$2x$肯定是$2x'$。一般来说$cx$肯定变成$cx'$，因为$A(cx)=c(AX)$。
• 如果向量$x,y$分别变成$x',y'$，那么他们的和$x+y$肯定变成$x'+y'$，因为$A(x+y)=Ax+Ay$。

矩阵乘法进行变换的时候施加这些规则，第二个规则包含第一个($c=0$得到$A0=0$)，对于第三个规则，考虑$(4,0)$关于45 度直线的反射，它可以分成$(2,2)+(2,-2)$，而且这两部分互为反射。同样的考虑投影：先分成两部分，然后分别投影并将投影相加。这些规则应用在任何矩阵的变换上。

他们的重要性还体现在名字的：符合三条规则的变换叫做线性变换。这些规则可以总结为一个：

20、对于任意的数$c,d$和向量$x,y$，矩阵乘法满足线性规则：

A(cx+dy)=c(Ax)+d(Ay)(1)

$$\begin{equation}A(cx+dy)=c(Ax)+d(Ay)\tag1\end{equation}$$ 满足这个要求的任何变换$T(x)$ 是一个线性变换。

任何矩阵都产生一个线性变换，那么反过来说：每一个线性变化都对应一个矩阵吗？本篇文章就是找出这个答案：是的。这是步入线性代数的基础，从性质(1) 开始引申出许多其他结论。现在我们直接从矩阵开始，看看他们如何表示线性变换。

一个变换没必要必须从$R^n$变到相同的空间$R^n$，允许将$R^n$中的向量变成不同空间$R^m$中的向量，那就是$m\times n$矩阵所做的事！原始向量$x$有$n$ 个元素，变换向量$Ax$ 有$m$个元素，线性变换的规则同样满足长方形矩阵，所以他们也生成线性变换。

更进一步，线性条件(1)的操作有加法和标量乘法，但是$x,y$ 没有必要是$R^n$ 的列向量，这些不是唯一的空间，根据定义，任何向量空间都存在组合$cx+dy$，他们可以是多项式，也可以是矩阵，也可以是函数$x(t),y(t)$，只要变换满足(1)，那它就是线性的。

我们举一个空间$P_n$上的例子，这些向量是次数为$n$的多项式$p(t)$，他们看起来像$p=a_0+a_1t+\cdots+a_nt^n$，并且向量空间的维数是$n+1$(因为有常数项)。

例1：微分运算$A=d/dt$是线性的：

$$\begin{equation} Ap(t)=\frac{d}{dt}(a_0+a_1t+\cdots+a_nt^n)=a_1+\cdots+na_nt^{n-1}\tag2 \end{equation}$$

$A$的零空间是一维的常数空间：$da_0/dt=0$，列空间是$n$ 为空间$P_{n-1}$；方程(2)的右边一直在空间里。零度(=1)和秩(=$n$)的和是原始空间$P_n$的维数。

例2：从0到$t$的积分运算也是线性的：

$$\begin{equation} Ap(t)=\int_0^t(a_0+a_1t+\cdots+a_nt^n)dt=a_0t+\cdots+\frac{a_n}{n+1}t_{n+1}\tag3 \end{equation}$$

这次没有零空间(除了零向量外)但是积分没有得到$P_{n+1}$ 中的所有多项式，方程(3)的右边没有常数项，可以常数多项式在左零空间里。

例3：一个确定多项式像$2+3t$乘以多项式是线性的：

$$Ap(t)=(2+3t)(a_0+a_1t+\cdots+a_nt^n)=2a_0+\cdots+3a_nt^{n+1}$$

将$P_n$变换到$P_{n+1}$，除了$p=0$外没有零空间。

在这些例子中，线性都不太难验证，有些看起来还挺有趣。是金子总会发光，这种性质有点像自生的属性，不会因为外界条件而改变。无关怎样，变换有非常重要的性质。但是许多变化都不是线性的，例如平方多项式($Ap=p^2$)，或加一($Ap=p+1$)，或保持正系数($A(t-t^2)=t$)。只有线性变换才能得出矩阵。

矩阵表示变换

线性有个至关重要的结论：如果我们知道基中每个向量的$Ax$，那么我们就知道整个空间中每个向量的$Ax$。假设基包含$n$个向量$x_1,\ldots,x_n$，所以其他向量$x$都是基向量的组合，那么线性就确定了$Ax$：

$$\begin{equation} \text{如果}x=c_1x_1+\cdots+c_nx_n,\text{那么} Ax=c_1(Ax_1)+\cdots+c_n(Ax_n)\tag4 \end{equation}$$

变换确定了基向量后，根据线性就已经确定了其他向量。对于两个向量$x,y$，根据(1)将得到(4)中的条件，对于基来说，这些向量的变换是比较自由的，但是当他们确定以后，每个向量的变换就确定了！

例4：什么样的线性变化将$x_1,x_2$ 变成$Ax_1,Ax_2$？

$$x_1= \begin{bmatrix} 1\\0 \end{bmatrix} \text{变成} Ax_1= \begin{bmatrix} 2\\3\\4 \end{bmatrix}; x_2= \begin{bmatrix} 0\\1 \end{bmatrix} \text{变成} Ax_2= \begin{bmatrix} 4\\6\\8 \end{bmatrix}$$

满足条件的矩阵为：

$$A= \begin{bmatrix} 2&4\\3&6\\4&8 \end{bmatrix}$$
我们从另一个基 $(1,1),(2,-1)$开始， $A$是唯一的线性变换：
$$A\begin{bmatrix} 1\\1 \end{bmatrix}= \begin{bmatrix} 6\\9\\12 \end{bmatrix} \quad A\begin{bmatrix} 2\\-1 \end{bmatrix}= \begin{bmatrix} 0\\0\\0 \end{bmatrix}$$

加些来我们找出表示微分和积分的矩阵。首先我们必须确定一个基，对于3次多项式，很自然的选择四个基向量：

$$p_1=1,\quad p_2=t,\quad p_3=t^2,\quad p_4=t^3$$

基不是唯一的，但是某些选择确实必须的而且也是最方便的。这四个基向量的导数是$0,1,2t,3t^2$：

$$\begin{equation} d/dt\quad Ap_1=0,\quad Ap_2=p_1,\quad Ap_3=2p_2,\quad Ap_4=3p_3\tag5 \end{equation}$$

$d/dt$是一种运算，就像矩阵一样，但是是什么样的矩阵呢？考虑通常的四维空间，坐标向量为$p_1=(1,0,0,0),p_2=(0,1,0,0),p_3=(0,0,1,0),p_4=(0,0,0,1)$，由(5)确定的矩阵是：

$$A_{diff}=\begin{bmatrix} 0&1&0&0\\0&0&2&0\\0&0&0&3\\0&0&0&0 \end{bmatrix}$$

$Ap_1$是第一列，也就是零，$Ap_2$是第二列，也就是$p_1$，$Ap_3$是$2p_2$，$Ap_4$是$3p_3$，零空间包含$p_1$，列空间包含$p_1,p_2,p_3$(立方的导数是平方)。根据线性，像$p=2+t-t^2-t^3$的导数可以确定出来：

$$\frac{dp}{dt}=Ap\to \begin{bmatrix} 0&1&0&0\\0&0&2&0\\0&0&0&3\\0&0&0&0 \end{bmatrix} \begin{bmatrix} 2\\1\\-1\\-1 \end{bmatrix} =\begin{bmatrix} 1\\-2\\-3\\0 \end{bmatrix} \to 1-2t-3t^2$$

总而言之，矩阵携带了所有的信息，如果基和矩阵都是已知的，那么每个矩阵的变换就是已知的。

信息编码很容易，将一个空间变换到它本身，一个基就足够了，从一个空间到另一个空间的变换需要其他的基。

21、假设向量$x_1,\ldots,x_n$是空间$V$的一个基，向量$y_1,\ldots,y_m$是$W$的一个基，从$V$到$W$的线性变换$T$用$A$来表示，将$T$应用到第$j$ 个基向量$x_j$得到第$j$列，将$T(x_j)$写成$y$组合的形式为：

$$\begin{equation}T(x_j)=Ax_j=a_{1j}y_1+a_{2j}y_2+\cdots+a_{mj}y_m\tag6\end{equation}$$

对于微分矩阵，列1来自于第一个基向量$p_1=1$，它的导数为0，所以列1为0，最后一列来自$(d/dt)t^3=3t^2$。因为$3t^2=0p_1+0p_2+3p_3+0p_4$，所以最后一列包含0,0,3,0，法则(6)一次得到矩阵的一列。

对于积分同样如此，它是从三次方到四次方，也就是$V=P_3$ 到$W=P_4$，所以我们需要$W$的一组基，很自然的选择是$y_1=1,y_2=t,y_3=t^2,y_4=t^3,y_5=t^4$，也就是四次多项式。应用积分到$V$ 中每个基向量得：

$$\int_0^t1dt=t\quad or\quad Ax_1=y_2,\ldots,\int_0^tt^3dt=\frac{1}{4}t^4\quad or\quad Ax_4=\frac{1}{4}y_5$$

$$A_{int}=\begin{bmatrix} 0&0&0&0\\1&0&0&0\\0&\frac{1}{2}&0&0\\0&0&\frac{1}{3}&0\\0&0&0&\frac{1}{4} \end{bmatrix}$$

积分和微分时逆运算，或者说从微分得到的积分可以还原到原来的函数，为了用矩阵表示，我们需要将微分矩阵变为$4\times 5$:

$$A_{diff}=\begin{bmatrix} 0&1&0&0&0\\0&0&2&0&0\\0&0&0&3&0\\0&0&0&0&4 \end{bmatrix} \quad A_{diff}A_{int}=\begin{bmatrix} 1&&&\\&1&&\\&&1&\\&&&1 \end{bmatrix}$$

微分是积分的左逆，长方形矩阵不可能两边同时有逆！所以反过来$A_{int}A_{diff}=I$是不成立的，$5\times 5$的话在第一行得到零，常数的导数为零，而$A_{int}A_{diff}$的其他行和单位矩阵一样，因为$t^n$微分后在积分还是$t^n$。

旋转矩阵Q，投影矩阵P，反射矩阵H

本部分我们介绍90度的旋转矩阵，向$x$轴的投影矩阵和45度线的反射矩阵，他们的矩阵都很简单：

$$Q=\begin{bmatrix} 0&-1\\1&0 \end{bmatrix} \quad P=\begin{bmatrix} 1&0\\0&0 \end{bmatrix} H=\begin{bmatrix} 0&1\\1&0 \end{bmatrix}$$

在$x-y$平面上的基本线性变换都是比较简单的，但是旋转其他角度，投影到任何一条线上，沿任何线做反射也是很容是可视化的，他们依然是线性变换，原点都是固定的：$A0=0$，肯定能用矩阵来表示。使用自然基$(1,0)^T,(0,1)^T$就可以找到这些矩阵。

1、旋转矩阵，图2所示旋转角度为$\theta$，同时也显示了对两个基向量的效果。第一个变成$(\cos\theta,\sin\theta)$，长度为1保持不变；第二个基向量变成$(-\sin\theta,\cos\theta)$，根据规则(6)，这些数放到矩阵的列中(我们用$c,s$分别表示$\cos\theta\sin\theta$)：

$Q_{\theta}$的逆等于$Q_{\theta}$吗？是的。

$$Q_{\theta}Q_{-\theta}=\begin{bmatrix} c&-s\\s&c \end{bmatrix} \begin{bmatrix} c&s\\-s&c \end{bmatrix} =\begin{bmatrix} 1&0\\0&1 \end{bmatrix}$$

$Q_{\theta}$的平方等于$Q_{2\theta}$吗？是的。

$$Q_{\theta}^2=\begin{bmatrix} c&-s\\s&c \end{bmatrix} \begin{bmatrix} c&-s\\s&c \end{bmatrix} =\begin{bmatrix} c^2-s^2&-2cs\\2cs&c^2-s^2 \end{bmatrix} =\begin{bmatrix} \cos2\theta&-\sin2\theta\\ \sin2\theta&\cos2\theta \end{bmatrix}$$

$Q_{\theta}$和$Q_{\varphi}$的乘积等于$Q_{\theta+\varphi}$吗？是的。

$$Q_{\theta}Q_{\varphi}=\begin{bmatrix} \cos\theta\cos\varphi-\sin\theta\sin\varphi&\ldots\\ \sin\theta\cos\varphi+\cos\theta\sin\varphi&\ldots \end{bmatrix} =\begin{bmatrix} \cos(\theta+\varphi)&\ldots\\ \sin(\theta+\varphi)&\ldots \end{bmatrix}$$

最后一种情况包含前两种情况，当$\varphi=-\theta$时就是第一种情况，当$\varphi=+\theta$时就是第二种情况。这三个方程由三角恒等式确定，毫无例外所有答案都是肯定的，矩阵乘法定义的非常精确，这样的话他们的乘积就对应着变换的乘积。

22、假设$A,B$分别是从$V$到$W$和从$U$到$V$的线性变换，他们的乘积$AB$从$U$的一个向量$u$开始，变成$V$中的$Bu$，最后是$W$中的$ABu$。组合$AB$依然是线性变换(从$U$到$W$)，它的矩阵是矩阵$A,B$的乘积。

对于$A_{diff}A_{int}$，这个组合变换得到单位矩阵($A_{int}A_{diff}$将常数消灭掉了)。对于两个旋转操作，乘法的顺序无所谓，那么$U=V=W$是$x-y$平面，$Q_{\theta}Q_{\varphi}$和$Q_{\varphi}Q_{\theta}$是一样的。对于一个旋转和一个反射操作，顺序不同结果就不同。

注意：为了构建矩阵，我们需要$V,W$的基，然后$U,V$的基。为了跟$V$保持一样的基，矩阵乘法直接从$U$的基变成$W$的基，如果我们知道了变换$A$的矩阵(我们叫做$[A]$)，那么规则22就变得非常简洁：$[AB]=[A][B]$，前面讲过的乘法规则完全由这个要求确定——它肯定对应着线性变换的乘积。

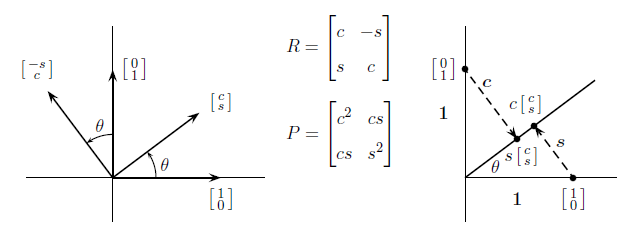
图2：旋转矩阵(左)，反射矩阵(右)

2、投影矩阵，图2也给出了$(1,0)$到$\theta$直线的投影，投影长度是$c=\cos\theta$，注意投影点不是$(c,s)$；向量长度为1，所以我们必须乘以$c$。同样，$(0.1)$的投影长度为$s$，投影点是$s(c,s)=(cs,s^2)$，它是投影矩阵$P$的第二列：

$$p=\begin{bmatrix} c^2&cs\\cs&s^2 \end{bmatrix}$$

这个矩阵没有逆，因为这个变换不是可逆的。垂线上的点映射到原点上；这条线是$P$的零空间。$\theta$线上的点映射到自身！对他们进行两次映射效果和一次是一样的，也就是$P^2=P$：

$$P^2=\begin{bmatrix} c^2&cs\\cs&s^2 \end{bmatrix}^2 =\begin{bmatrix} c^2(c^2+s^2)&cs(c^2+s^2)\\cs(c^2+s^2)&s^2(c^2+s^2) \end{bmatrix} =P$$

其中$c^2+s^2=\cos^2\theta+\sin^2\theta=1$。投影矩阵等于它自身的平方。

3、反射矩阵，图3给出了$(1,0)$关于$\theta$线的反射，反射的长度等于原始长度，就像旋转操作那样——但是这里$\theta$线保持不变。垂线的方向反转了，

$$H=\begin{bmatrix} 2c^2-1&2cs\\2cs&2s^2-1 \end{bmatrix}$$

矩阵$H$有一个特别的性质：$H^2=I$，两次反射回到原始情况。一次反射是自身的反转：$H=H^{-1}$，从几何上看非常明显。反射和映射的关系式：$H=2P-I$，这意味着$Hx+x=2Px$——反射的加上原始的等于投影的两倍，另外这还证实了$H^2=I$

$$H^2=(2P-I)^2=4P^2-4P+I=I,\quad \text{因为}P^2=P$$

图3：反射：几何和矩阵

我们需要强调一下，矩阵依赖于所选择的基。假设第一个基在$\theta$线上，第二个基向量跟它垂直：

• 对于投影，这个矩阵按如下方式构建：第一列就是第一个基向量(投影到自身)，第二列就是投影为零的基向量。
• 对于反射，第二个基向量通过反射变成第一个向量的反方向，那个反射轴就是第二列。当矩阵$H,P$的基一样时，矩阵$H$依然满足$2P-I$。
• 对于旋转，矩阵不发生变换，跟之前一样。

选择一个最好的基明显是整个问题的核心，之后我们会形式介绍这个。

当线性变换不变时，基的改变会影响到矩阵，就像矩阵$A$变为$S^{-1}AS$，由此可见，一个变换是由不同的矩阵表示出来，之后要将的特征值理论会导出公式$S^{-1}AS$和最好的基。