漫步微积分三十七——力和功

首先提一个常识，在移动的对象上施加一个发力，如举起一块很沉的石头，我们感觉需要很大的力气或做功。在我们定义物理上功的概念之前，我们深信移动相同的距离，举起20磅的石头所做的功是l0磅的两倍，并且俱到3英尺所做的功是1 英尺的三倍。这些想法给出了我们基本的定义：如果恒力$F$作用的距离为$d$，那么这个过程中完成的功为力和它作用距离的乘积

$${work\ =force\ \cdot distance}$$

或者

$$\begin{equation} W=F\cdot d\tag1 \end{equation}$$

这里的力方形和运动方向一致。

正如我们所知，由于地球的吸引力，有“重量”的对象存在重力。对于处于或接近地球表面的物体，这个力基本上是大小恒定而且总是指向地心。因此，如果一箱重20磅的食品是从地上抬起放到一张3英尺高的桌子上，那么定义(1)告诉我们做了60$ft-lb$的功；但如果盒子抬进另一个房间但没有提高或降低它，放在一个架子上，那么这个操作完成后没有做功，因为盒子在力方向移动的距离为零。如果一台拖拉机拖动用恒力2牛拖动一块巨石走了18英尺，那么拖拉机所做的功为36$in-ton$(或3$ft-ton$)

这个定义只对恒力$F$满足。然而，在用力的过程中许多力都不保持恒定。对于类似的情况，我们可以将过程分成很多小部分然后通过积分得到总的功。

这种想法用下面拉伸弹簧的操作进行说明。

例1：某弹簧自然长度为$16in$。当它被拉伸到$x in$ 时，胡克定律指出弹簧的恢复力为$F=kx\ pounds$，其中$k$为常数，它称为弹力系数，可以认为是弹簧刚度的度量。对题中讨论的弹簧，需要$8\ lb$的力来才能将它延伸$2\ in$。那么，从自然长度拉伸到$24\ in$需要完成的功是多少？

解：首先，根据事实$x=2,F=8$可以求出$k$。$8=k\cdot 2$，所以$k=4,F=4x$。为了说明我们的想法，我们画一个自然长度下的弹簧，以及拉伸$x$时的状态(图1)。然后，我们想象弹簧拉伸很小的距离$dx$，那么在这距离增量内力变化很小，基本上可以认为是恒定的。所以这段距离做的功是

$$\begin{equation} dW=F\ dx=4x\ dx\tag2 \end{equation}$$

整个拉伸过程中所做的功为

$$W=\int dW=\int Fdx=\int_0^84xdx=2x^2\Big|0^8=128\ in-lb$$

因为弹簧从16增到24时$x$是从0增加到8，所以积分限为0到8。

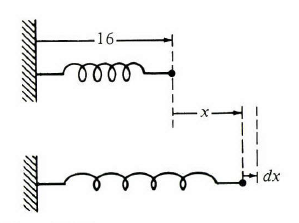
图1

用相似的方式，我们可以考虑，给定物体移动的方向作用在上面的力所做的功，这个力不限制必须是恒力，也可以是变化的力。如果我们引入$x$轴，从$x=a$移动到$x=b$的过程中力为$F(x)$，那么$dW=F(x)dx$是功的元素

$$\begin{equation} W=\int dW=\int_a^bF(x)dx\tag3 \end{equation}$$

给出了该过程的总功。这个公式既可以作为定义，也可以作为计算功的方法。下一个例子我们引用到不同的情景中。

例2：根据牛顿的万有引力定律，任何两个物质为$M$和$m$的物体互相之间存在吸引力$F$，它的大小与质量的乘积成正比，与它们之间距离$r$的平方成反比

$$F=G\frac{Mm}{r^2}$$

其中$G$叫做引力常数。如果$M$看做一个质点，那么将$m$从$r=a$移动到$r=b,a<b$需要做多少功？

解：功的元素为

$$\begin{equation} dW=F\ dr=GMm\frac{dr}{r^2}\tag4 \end{equation}$$

所以总功为

$$W=\int dW=GMm\int_a^b\frac{dr}{r^2}=GMm\left(-\frac{1}{r}\right)\Big|_a^b=GMm\left(\frac{1}{a}-\frac{1}{b}\right)$$

考虑如果最终位置$r=b$非常远，以致于$b\to \infty$，那么功$W$将接近极限值$GMm/a$。将$m$从$r=a$移到无穷远处(也就是完全将两个物体分开)所需要做的功；它叫做两个粒子的势能。

前面处理的例子都是距离一定，作用的力是变化的。接下里的例子与此不同，物体的一部分在同一个力下移动不同的距离，总功可以通过计算部分功的和求出来。

例3：考虑一个底边半径为$r$高为$h$的圆柱体，其中水深为$D$(图2)。那么将水移到桶的边缘需要做多少功？(通常我们用$w$表示水的质量密度(weight-density) 来表示，也就是单位体积的质量)

解：这个问题的本质是每一滴水必须从初始位置移到桶的边缘。对边缘下方同一距离的所有水滴，这个过程做的功是一样的。这表明我们可以考虑很薄的水平圆柱层，在高为$x$处的厚度为$dx$，那么将这部分移到桶边缘的所做的功是$dW$，同样对其它层也用这种方法，然后从$0$ 到$D$进行相加记得总功。另外从图中可以看出，每层的体积为$\pi r^2dx$，所以质量为$w\pi r^2dx$，功的元素为

$$\begin{equation} dW=w\pi r^2dx\cdot(h-x)\tag5 \end{equation}$$

因此总共为

$$\begin{align*} W=\int dW &=w\pi r^2\int_0^D(h-x)dx\\ &=w\pi r^2(hx-\frac{1}{2}x^2)\Big|_0^D=w\pi r^2(hD-\frac{1}{2}D^2) \end{align*}$$

重新强调一下：本例题方法的关键是薄的圆柱层内所有的水移动了相同的距离。

我们应该看到定义(1)是这些例子的关键所在。公式(2)(4)(5)仅仅是(1)在不同情景下的版本。

接下来我们讨论另一个重要的概念：能量

考虑作用变力$F$作用在质量为$m$的物体上移动了一段距离，这里我们采用$x$轴。这个力不仅做了功，而且还产生了加速度$dv/dt$，根据牛顿第二运动定律

$$\begin{equation} F=m\frac{dv}{dt}\qquad where\ v=dx/dt\tag6 \end{equation}$$

由力产生的加速度改变了物体的速度，也叫作动能或能量，它的定义式为

$$kinetic\ energy\ =\frac{1}{2}mv^2$$

现在我们证明下面的力学定理：

上面描述的过程中，力$F$所做的功等于物体动能的变化量；特别地，如果物体开始是静止的，那么力所做的功等于物体获得的动能。

这个证明很容易。我们首先将(6)写为

$$F=m\frac{dv}{dt}=m\frac{dv}{dx}\frac{dx}{dt}=mv\frac{dv}{dx}$$

利用公式(3)得

$$\begin{align*} W=\int_a^bFdx &=\int_a^bmv\frac{dv}{dx}=dx=\int_{v_a}^{v_b}mvdv\\ &=\frac{1}{2}mv^2\Big|_{v_a}^{v_b}=\frac{1}{2}mv_b^2-\frac{1}{2}mv_a^2 \end{align*}$$

所以功$W$等于动能的变化量。

图2

注解：对某些物理情况，它可能介绍势能的概念，下面，我们就非常简明的解释一下。为了计算(7)我们使用公式(3)，假定未指定的力$F$是连续函数且只依赖$x$轴，其区间为$a\leq x\leq b$。(注意，摩擦力没有这种属性；因为它不仅取决于物体$m$的位置，还有移动方向)。这个假设保证存在函数$V(x)$使得$dV/dx=-F(x)$。因此我们可以用另一种方式来计算功$w$如下所示：

$$\begin{align} W=\int_a^bF(x)dx &=\int_a^b-F(x)dx=V(x)\Big|_b^a\nonumber\\ &=V(a)-V(b)\tag7 \end{align}$$

所以(7)可是写成

$$\frac{1}{2}mv_b^2-\frac{1}{2}mv_a^2=V(a)-V(b)$$

或者

$$\begin{equation} \frac{1}{2}mv_b^2+V(b)=\frac{1}{2}mv_a^2+V(a)\tag8 \end{equation}$$

(9)的左边我们去掉下标，并用$V(x)$代替$V(b)$，这样做是为了强调$v,V(x)$是变量；在右边$v_a,V(a)$保持不变。于是(9)就写成

$$\begin{equation} \frac{1}{2}mv^2+V(x)=\frac{1}{2}mv_a^2+V(a)=E\tag9 \end{equation}$$

其中常数$E$叫做物体的总能量。函数$V(x)$叫做物体的势能，(10)表明动能和势能的和是常数。这就是能量守恒定律，经典物理学中基本原则之一。

从(10)中可以看出，如果$F(x)$作功，那么动能将增加，势能同样如此。所以可以看做势能转化成等量的动能。

我们指出$V(x)$的定义表明它这个函数通过增加一个常数就能确定，所以为了方便，在任何特定情况下我们都选择零势能，此外，大家可能疑惑定义$V(x)$时候的代数符号，这样做的目的是保证(10)中出现的是正好而不是负号，这样的话，我们可以说动能和势能之和而不是它们的差是常数。

例4：从物理上看，人类的心脏是一种泵。血液通过二尖瓣(图3)进入左心室，然后通过主动脉瓣迸出到身体各处。每次收缩期间的舒张压是80$mm\ Hg$
收缩压是120$mm\ Hg$。现在我们计算一次心跳左心室做的功，假设心室的体积在收缩的时候减少约75$cm^3$。我们需要知道$100\ mm\ Hg\cong 1.33\times 10^5\ dynes/cm^2$。

为便于理解泵的工作原理，我们将心脏想象成如图所示的从$x=0$到$x=a$的活塞运动，而不是肌肉收缩。如果$A$是活塞头的面积，那么$aA=75$。从图4可以看出活塞工作的压强$P(x)$

$$P(x)=\frac{40}{a}x+80$$

我们现在把这一切放在一起，观察到一次向上运动的过程中施加在活塞上的力是$P(x)A$，所以这个过程中所做的功为

$$\begin{align*} W=\int_0^aP(x)Adx &=A\int_0^a\left(\frac{40}{a}x+80\right)dx\\ &=A\left(\frac{20}{a}x^2+80x\right)\Big|_0^a=100aA\\ &\cong(1.33\times 10^5\ dynes/cm^2)\cdot(75\ cm^3)\\ &\cong10^7\ dyne-cm\\ &\cong1\ joule\\ &\cong 0.74\ ft-lb \end{align*}$$

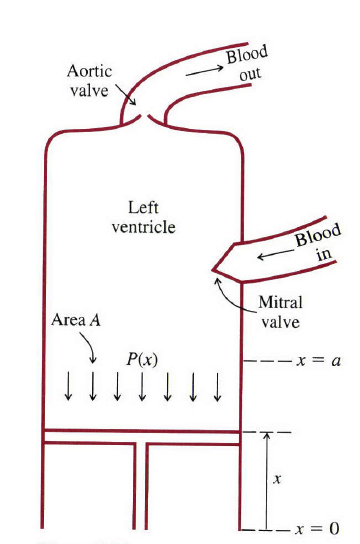
图3

对一个体重120磅，脉率为60的人来说，我们可以利用计算器快速算出一天24小时心脏做的功可以将这个人垂直举起500 多$ft$。人类心脏是重要的器官，但是被我们低估了！

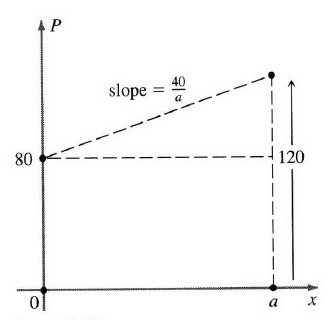
图4