统计学：第六章-总体均数得估计

统计学：第六章-总体均数得估计

雪柯

大工生物信息 提笔为写给奋进之人

已关注

致知计划 · 科学季收录

点击报名

29 人赞同了该文章

该书作者：李晓松 本文引自医学统计学教材，作为统计学入门经典教程，讲解通俗易懂，易于理解

首先简单列一下本章的思维导图

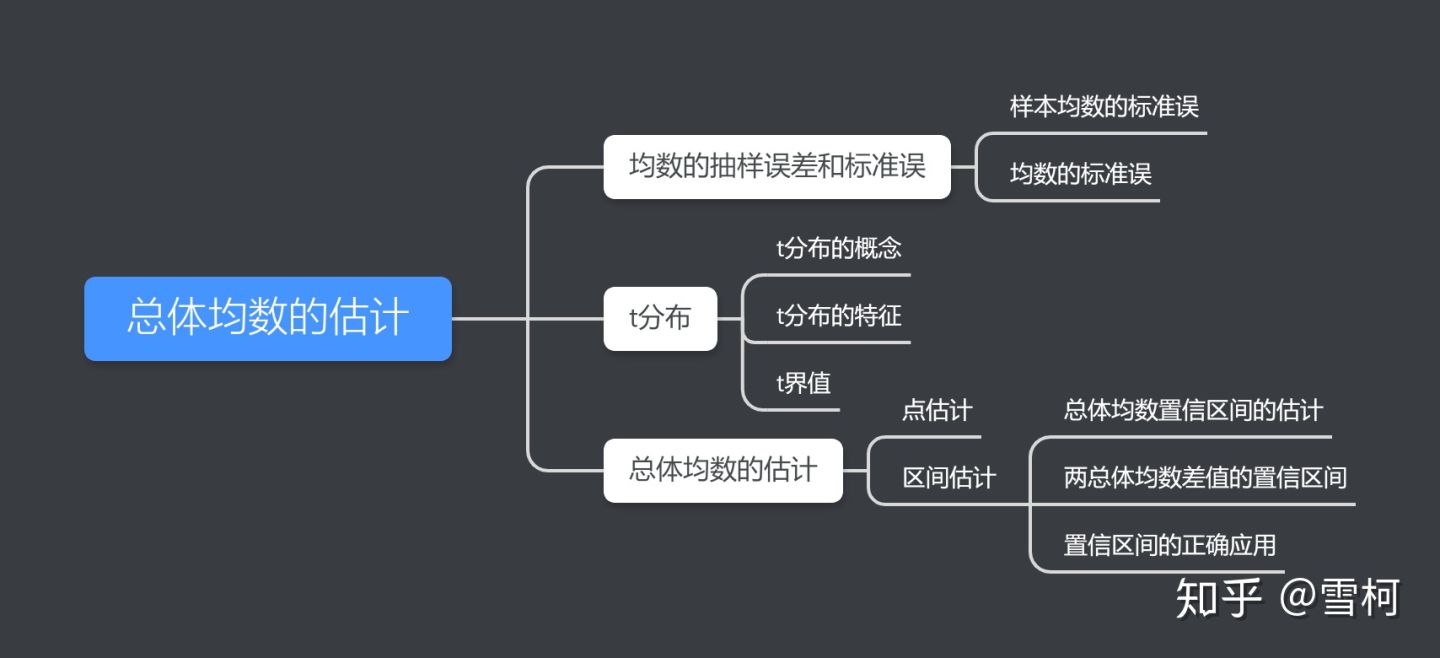
自本章开始进人统计推断部分的讨论。由样本数据对未知的总体指标作出估计或比较称为统计推断，参数估计和假设检验是统计推断的两个重要领域，本章介绍参数估计中总体均数的估计。

第一节:均数的抽样误差和标准误

在抽样研究中，由于同质总体中的个体存在差异，即个体变异，因而从同一总体中随机抽取若干份样本，样本均数往往不等于总体均数，且各样本均数之间也存在差异。这种由个体变异 产生的、随机抽样引起的样本统计量与总体参数间的差异称为抽样误差。在抽样研究中，抽样误差是不可避免的，但其大小可以通过样本统计量的抽样分布进行估计。

一、样本均数的抽样分布

现以计算机模拟实验来说明样本均数的抽样分布规律

模拟实验1：从均数μ=4.5，标准差σ的正态总体中作随机抽样，规定样本含量分别为 5、10、15、20 。每种样本含量均重复抽取1000次，结果可得到4个不同样本含量的样本均数的抽样分布图，如图6-1所示

图片来源：医学统计学书籍

当样本含量为20时，随机抽取100个样本，观察其样本均数、标准差及其总体均数的5 % 置信区间见表6.1，样本均数的频数分布见表6.2

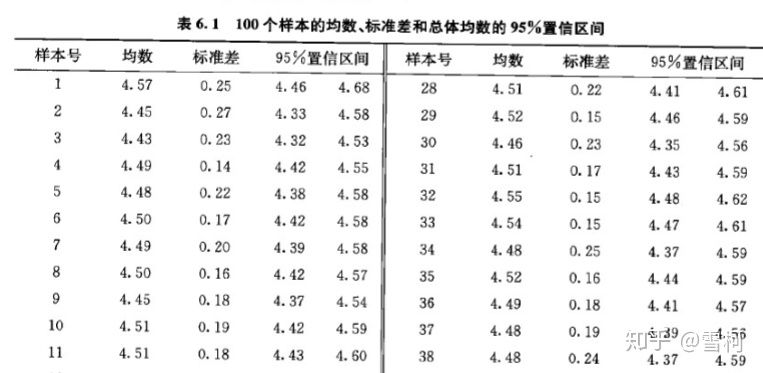
图片来源：医学统计学书籍

图片来源：医学统计学书籍

可见，样本均数的抽样分布具有以下特点:

1、各样本均数未必等于总体均数；

2、样本均数之间存在差异；

3、样本均数的分布很有规律，围绕着总体均数45，中间多、两边少左右对称，基本服从正态分布；

4、样本均数的变异范围较之原变量的变异范围小；

5、随着样本含量的增加，样本均数的变异范围逐渐缩小。

模拟实验2：从非正态总体中抽样，观察其样本均数的抽样分布。非正态总体的分布如图 6.2所示。

图片来源：医学统计学书籍

规定样本含量分别为5,10,20,50，每种样本含量均重复抽取1000次，结果也可得到4个不同样本含量的样本均数的抽样分布图，如图6.3所示。

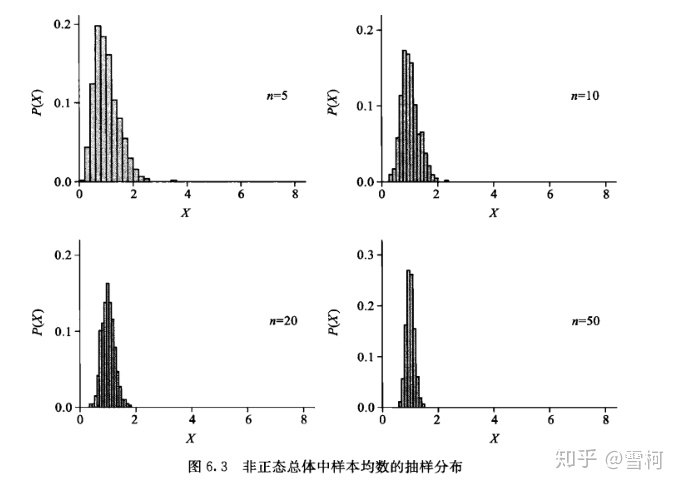
图片来源：医学统计学书籍

可见从非正态总体中抽样，样本均数的抽样分布也基本具有上述特点，随着样本含量增大，样本均数的分布逐渐近似正态分布。

二、均数的标准误

由于随机抽样造成的样本均数与急体均数的差别，即为样本均数的抽样误差。样本均数的标准差称为均数的标准误。用符号 表示，它说明各样本均数 围绕总体均数μ的离散程度，可用来描述样本均数的抽样误差大小 。

根据数理统计的中心极限定理从均数为μ，标准差为σ的正态总体中进行独立随机抽样，其样本均数服从均数为μ标准差为   的正态分布；即使是从非正态总体中进行独立随机抽样，当样本含量逐渐增大时（n>=50 )，其样本均数的分布逐渐逼近于均数为μ标准差为 的正态分布，因此样本均数的标准误   的计算公式为：

  =   （6.1）

 越大，样本均数的分布越分散，样本均数与急体均数的差别越大，抽样误差越大，由样本均数估计总体均数的可靠性越小，反之， 越小，样本均数的分布越集中，样本均数与总体均数 的差别越小，抽样误差越小，由样本均数估计总体均数的可靠性越大 。由式6.1可知 的大小与   成正比，与   成反比。因此在实际工作中，可通过适当增加样本含量来减少标准误，降低抽样误差。

在抽样研究中，总体标准差   常常未知，常用样本标准差S作为   的估计值，因而得到均数标准误的估计值   ．其计算公式为：

  （6.2）

由式子6.2可见，仅进行一次抽样，得到一个样本均数   和样本标准差S，即可估计样本均数的抽样误差大小。

例6.1 随机抽取某地正常成年男性200名，测得其血清胆固醇的均数为3.64mmol/L,标准差为1.20mmol/L，试估计其抽样误差。

由式6.2得  =   =0.085（mmol/L)

例6.2 某研究人员查阅文献发现同类文献资料的表述不同，见表6.3，感到疑惑。请问两者的表述有何区别？

图片来源：医学统计学书籍

两种表述的不同在于文献1用的是均数和标准差，表示的是收缩压的集中位置和离散程度，文献2用的是均数和标准误，表示的是收缩压的平均水平及其抽样误差大小。标准差和均数的标准误的区别和联系见表6.4。

图片来源：医学统计学书籍

第二节：t分布

一、 t分布的概念

第四章介绍正态分布时，曾提到标准正态变换，即对服从正态分布N（μ，   ）的随机变量X 采用z=   变换，则可将其转化为标准正态分布N（0，1）。

通过本章前一节样本均数抽样分布的学习，我们知道从正态总体中随机抽取的样本均数   服从总体均数为μ，总体标准差为   的正态分布。当然也可以对样本均数 这个正态变量进行 Z变换，这时的z=  。同样，经过Z变换，正态分布N（μ，   )转化为标准正态分布N（0，1）,即Z分布。

由于实际研究工作中，   未知的情形是常见的，因此上述Z变换中只能以   代替 ,由此 求得的变换 会不同于 。显然，后者的理论标准误 =   是个常量， 随正态总体的确定而确定；但前者的样本标准误 = 却不然，S会因样本不同而不尽相同，即 有变异。故 不再服从标准正态分布，而服从t分布，即：

t= = ，   (6.3)

t分布主要用于总体均数的区间估计及t检验等。最早由英国统计学家W.S.Gosset于1908年用笔名"Student"发表的论文提出来的，因此，t分布又称Student分布。

  为自由度，在数学上指能自由取值的变量个数，例如在X+Y=8中，有两个变量，由于受到和数8的限制，只有一个变量能自由取值，这时 =1；而在X+Y+Z=15 中。由于受到和数15的限制，三个变量中只有两个变量能够自由取值，这时 =2 。数理统计中计算自由度的一般公式为：

  (6.4)

式中n为样本含量，k为计算某一个统计量时需要用到其他独立统计量的个数。如式6.3中统计量t的计算，因S的计算也用到   ，故其他独立统计量只有 一个，其自由度 。

二、t分布的特征

t分布是与自由度   有关的一簇曲线。由图6.4给出的   , 时的三条t分布曲线 可以看出，当自由度 不同时，曲线的形状不同。t分布与标准正态分布相比，其图形有如下 特征：

图片来源：医学统计学书籍

1、以t=0为中心左右对称的单峰分布；

2、t分布曲线的形态取决于自由度大小。自由度越小，曲线的峰部越低，尾部越高；随着自由度的增大，t分布逐渐逼近标准正态分布当自由度趋于oo时，t分布就是标准正态分布。

三，t界值

当   确定后，t分布曲线下，双侧尾部的面积或单侧尾部的面积为指定概率   时，横轴上相应 的t界值是多少？这是统计应用中经常需要解答的问题。为了应用方便，统计学家编制了t届值表，见附录3。

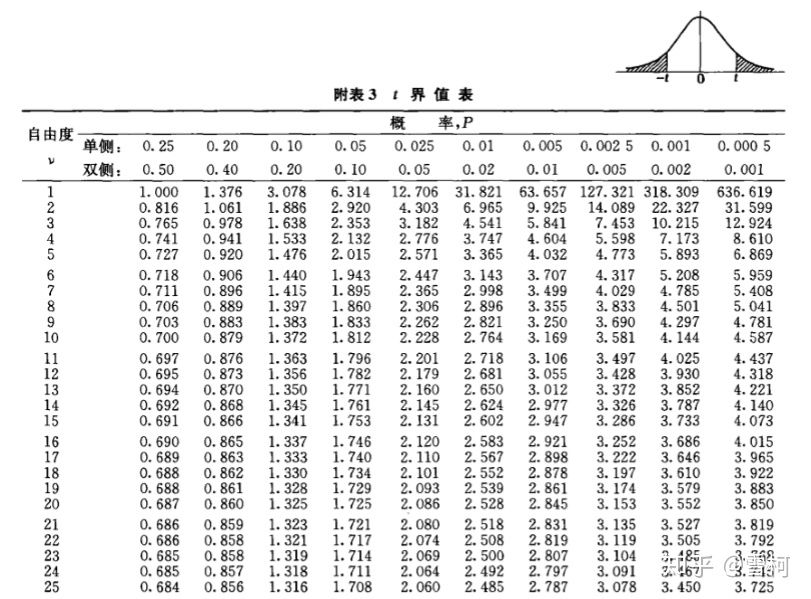
图片来源：医学统计学书籍

该表横标目为   ，纵标目为概率，单侧概率或单尾概率是指t分布曲线下一侧尾部面积，双侧概率或双尾概率是指t分布曲线下两侧尾部面积之和，即表右上角图例中阴影部分。表中数字表示，当自由度   与概率   给定时，对应的t界值。一般，与单侧概率相对应的t界值记作   ，与双侧概率相对应的t界值记作   。由于t分布以t=0为中心对称，表中只列出正值，故查表时，不管t值正负，只用绝对值

由t界值表还可看出：①同一概率下，自由度越大，   越小;②同一自由度下， 越大，概率P值越小;③同一自由度下，双侧概率为单侧概率的2倍时，所对应的t界值相等，如 = =1.725；④当   时的t界值即为相应概率下的Z值。

第三节总体均数的估计

参数估计是指用样本统计量来估计总体参数，有点估计和区间估计两种方法。点估计是用样本统计量直接作为总体参数的估计值。区间估计是给出被估计参数的可能的数值范围。

一、点估计

例如，某地区2006年所有了岁男童的身高值是一个总体，其总体平均身高   与   均未知。 为此，随机抽取该地150例7岁男童，得到平均身高   =123.8cm，标准差S=4.7cm。此时，可用样本均数123.8cm作为总体均数 的一个估计值，即认为该地区所有7岁男童的平均身高为123.8cm。同样，也可以用样本标准差4.7 cm作为总体标准差 估计值，这种方法，思维朴 素，结果直观。

但我们知道，上述问题中，总体参数 是确定的值，而样本均数 是随机变量。若从该总体中再随机抽取一份样本，得到平均身高 =126.9cm，并以126.9cm作为总体平均身高的点估计。

基于上述两个样本做出的点估计，我们关心的是哪一份样本的估计更接近总体均数，或者哪 一个结论更可信，这是难以回答的。点估计虽然方法简单，但它没有充分利用样本信息，不能反映抽样误差的影响，因此无法评价这种估计的可信程度。

二、区间估计

所谓区间估计是指按一定的概率（1一  )，估计总体参数的所在范围，这个范围称为参数的置信区间。概率（1一  )称为置信度，也可表示为 100 (1一 ) %，常取95％或99 %，如果没有特别说明，一般取双侧95％。置信区间通常由两个置信限构成。其中较小者称为置信下限   ，较大者称为置信上限记为 。严格地讲，置信区间（ ， ）是一个开区间，不包括置信下限和置信上限两个值。

（一）总体均数置信区间的估计

根据均数的抽样分布理论：从正态总体N（μ，   ）中随机抽取样本含量为n的一个样本，当   未知，由样本标准差S代替   时，统计量 t=  服从自由度为 的t分布。

根据t分布原理则有：

即：  

于是总体均数   的双侧(1-   )的置信区间的计算公式为：

  ) (6.5)

其中，   为自由度，   表示当自由度为   时的t分布曲线下，两侧尾部面积各占   /2所对应的右尾临界值，可查t界值表获得。

 为置信区间的下限， 为置信区间的上限。

1-   为置信度，当 =0.05时，置信度为0.95。当 =0.001时．置信度为0.99 。

当样本含量较大时例如n> 100，t分布逼近标准正态分布，此时，可用标准正态分布的z值代替t值，得到总体均数的双侧（1-   ）置信区间为：

  (6.6)

其中   为标准正态曲线下两侧尾部面积各占   / 2所对应的右尾临界值，即t界值表中   时的临界值。当双侧   =0.05时。 =1.96；双侧   =0.01时， =2.58。

当总体标准差   未知时，不管样本含量n多大，总体均数   的置信区间均可由式6.5计算。虽然在大样本时，可采用正态近似法，由式6.6做出估计，但式6.5计算的置信区间更加确切。

例6.3 在某地成年男子中随机抽取25人，测其脉率，得到脉率均数为72次／min，标准差为8次／min 。试估计该地成年男性脉率总体均数的95％置信区间。

本例中，n=25，   =72，S=8

  取双侧0.05，以   =25-1=24查t界值表得   ，按式6.5计算：

根据样本计算，可推断该地成年男性脉率总体均数的95%置信区间为（68.7 , 75.3)次/min 。

例6.4 随机抽取某地200名40岁以上正常人，测定其空腹血糖值．求得   =4.91mmol/L，S=0.72mmol/L，试估计该地40岁以上正常人群空腹血糖值的总体均数的95%置信区间。

本例中，n=200，   =4.91，S=0.72

由于n较大故可用正态近似法，   取双测0.05，   =1.96,按式6.6计算置信区间：

根据样本计算，可推断该地40岁以上正常人平均空腹血糖值的95％的置信区间为（4.81 , 5 01 ) mmol/L

本例若按式6.5 t分布法计算，则按   =200-1=199查t界值表得   =1.972，故 95％置信区间也为（4.81 , 5.01 ) mmol / L

注意：附表3没有列出 的值，故用就近的 值近似替代，本书余处同

（二）两总体均数差值的置信区间

实际工作中，我们常需要估计两总体均数之差（  ）的大小，例如正常成年男、女的血红蛋白平均相差多少？糖尿病患者经某药物治疗后，试验组与对照组的总体血糖值平均降低多少？ 冠心病患者和正常人的血清胆固醇值平均相差多少？我们可以用两样本均数之差（  ）作为两总体均数之差（ ）的点估计。同理，点估计没有考虑抽样误差的大小，需估计两总体均数之差的置信区间。

假设正态总体   和 ，当   , 均未知，但  = 时，则两总体均数之差 （ ）的双侧（1-   ）置信区间为：

    (6.7)

其中t值的自由度   , 称为为两均数之差的标准误，由下式计算：

  (6.8)

而   称为合并方差，是两样本方差 ， 的加权平均：

 =   (6.9)

例6.5 测定28例结核病患者和34例对照者的脑脊液中镁（mmol / L)的含量，结果见表 6.5，试估计结核病人和对照者的脑脊液中镁含量的总体均数之差的95％置信区间。

图片来源：医学统计学书籍

根据样本资料可得：

  =28，   =1.04，   =0.17

  =34，   =1.28，   =0.14

假定两组方差齐，由式6.9得

  =0.024

由式6.8得：

 =0.040

  取双测0.05，按照自由度  =60 查t界值表得  

由式子6.7得：

故两总体均数之差的95％置信区间为（0.16,0.32）mmol / L，可以认为结核病患者脑脊液中 的镁含量较对照人群平均低0.24 mmol / L,其95％置信区间为（0.16,0.32）mmol / L

（三）置信区间的正确应用

1、置信区间的含义

总体均数的95％置信区间的含义是从正态总体中重复100次抽样，每次样本含量均为n。每个样本均按   计算95％置信区间，则在这100个置信区间中理论上有95％个置信区间包含了总体均数（估计正确），而有5个置信区间未包含总体均数（估计错误），即犯错误的概率是5％。

但在实际应用中，只能依据一次抽样结果估计置信区间，如例6.3中95%置信区间为 ( 68.7 , 75.3）次／min，我们就认为该区间包含了总体均数μ。根据小概率事件在一次实验中几乎不可能发生的原理，该结论错误的概率等于0.05

从表6.1可以看出，尽管对某个置信区间来说，它要么包含了   ，要么不包含 。但对所有置 信区间来说．当   时，它们包含总体均数的概率为95 %

特别需要注意的是我们不能认为”总体均数以95％的概率落人置信区间内“，也不能认为 “有95％的总体均数在该区间内，而5%的均数不在该区间内”。因为对于一个确定的总体，总体均数也是确定的，且只有一个，对它无概率可言。置信区间的数值是随样本观察值而变化的，它们能否包含总体均数是个随机事件，例如建立100个置信区间，若有95个包含总体均数，我们则称全部区间包含总体均数的概率为95%。

2、置信区间的两个要素

当用区间估计的方法估计未知参数时，一方面我们希望建立的置信区间能以很大的概率包含进未知参数，另一方面又希望这个区间不能太宽，区间越宽说明估计的精确度越低。

总体均数的置信区间由两个要素来衡量。第一个要素是准确度，反映置信度 (1-   ）的大小，即置信区间包含总体均数的概率，若单纯考虑准确度，当然 (1-   ）越接近1越好。 例如，对于同一份资料，就准确度而言，99％的置信区间比95%写好。第二个要素是精确度或精密度，反映为置信区间的宽度，常用   来衡量。由于置信区间的宽度取决于   的大小，因此精确度与变量的变异度大小、样本例数和 (1-   ）的取值有关。当 (1-   ）确定 后，个体变异越大，区间越宽；样本含量越小，区间越宽。反之，区间越窄。从精确度的角度来看，置信区间的宽度愈窄愈好。当样本含量确定后，准确度和精确度是相互牵制的，若提高了置信度，置信区间势必增宽（即减小  但增大了t或Z)，精确度会下降，势必降低置信区间的实用价值。例如，对于同一份资料95％的置信区间的精确度比99％好。所以不能简单认为99％的置信区间优于95%置信区间。因此，实际工作中为了较好地兼顾准确度和精确度一般常用95% 置信区间

小结

1、由随机抽样速成的样本均数与总体均数的差别，称为样本均数的抽样误差。样本均数的抽样误差可以通过样本均数的抽样分布来度量。

2、样木均数的标准差称为标准误，可用来描述样本均数的抽样误差大小。标准误越小，样本均数与总体均数的差别越小，抽样误差越小由样本均数估计总体均数的可靠性越大。适当增大样本含量可以减少标准误。

3、样本均数   经过t变换服从t分布，t分布用于总体均数的估计和t检验等。

4、总体均数的估计有点估计和区间估计两种方法，总体均数的双侧（1-   ) 置信区间的估计方法：   未知：计算公式为 ；  未知而n较大：计算公式为 

编辑于 11-04