支持向量机(SVM,Support Vector Machine)算法是一种常见的分类算法,在工业界和学术界都有广泛的应用。特别是针对数据集较小的情况下,往往其分类效果比神经网络好。
1.SVM算法原理
SVM的原理就是使用分隔超平面来划分数据集,并使得支持向量(数据集中离分隔超平面最近的点)到该分隔超平面的距离最大。其最大特点是能构造出最大间距的决策边界,从而提高分类算法的鲁棒性。
1.大间距分类算法
假设要对一个数据集进行分类,如下图所示,可以构造一个分隔线把圆形的点和方形的点分开。这个分隔线称为分隔超平面(Separating Hyperplane)。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
class1 = np.array([[1, 1], [1, 3], [2, 1], [1, 2], [2, 2]])
class2 = np.array([[4, 4], [5, 5], [5, 4], [5, 3], [4, 5], [6, 4]])
plt.figure(figsize=(8, 6), dpi=144)
plt.title('Decision Boundary')
plt.xlim(0, 8)
plt.ylim(0, 6)
ax = plt.gca() # gca 代表当前坐标轴,即 'get current axis'
ax.spines['right'].set_color('none') # 隐藏坐标轴
ax.spines['top'].set_color('none')
plt.scatter(class1[:, 0], class1[:, 1], marker='o')
plt.scatter(class2[:, 0], class2[:, 1], marker='s')
plt.plot([1, 5], [5, 1], '-r')
plt.arrow(4, 4, -1, -1, shape='full', color='r')
plt.plot([3, 3], [0.5, 6], '--b')
plt.arrow(4, 4, -1, 0, shape='full', color='b', linestyle='--')
plt.annotate(r'margin 1',
xy=(3.5, 4), xycoords='data',
xytext=(3.1, 4.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'margin 2',
xy=(3.5, 3.5), xycoords='data',
xytext=(4, 3.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'support vector',
xy=(4, 4), xycoords='data',
xytext=(5, 4.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'support vector',
xy=(2, 2), xycoords='data',
xytext=(0.5, 1.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
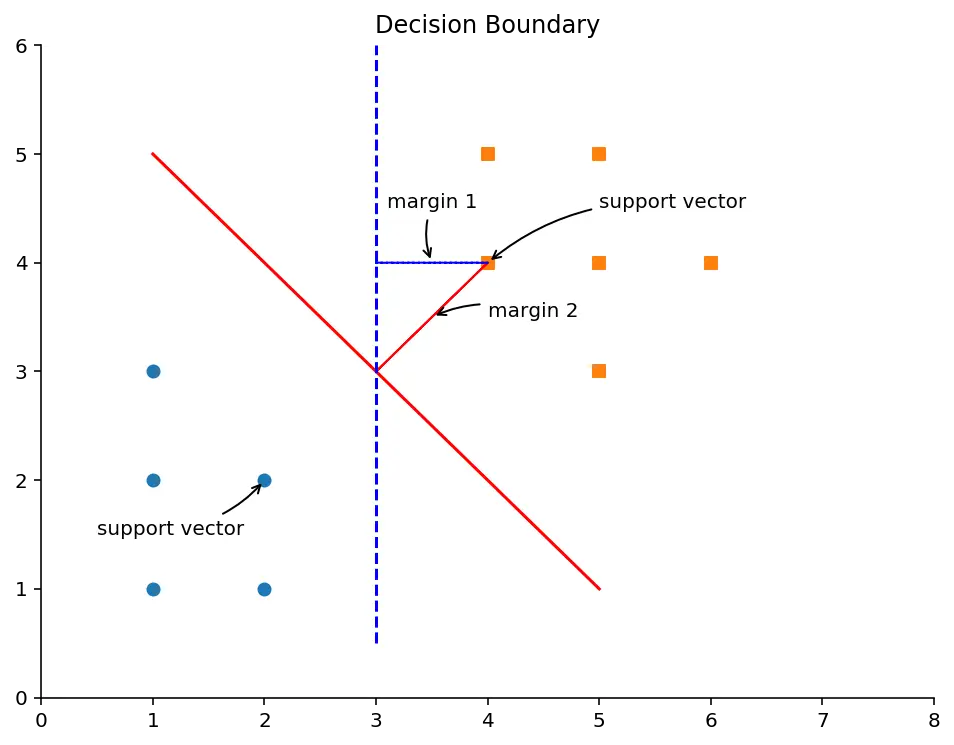
从上图可以明显地看出,实线的分隔线比虚线的分隔线更好,因为使用实线的分隔线进行分类时,离分隔线最近的点到分隔线的距离最大,即margin2>margin1。这段距离的2倍称为间距(margin)。那些离分隔超平面最近的点,称为支持向量(Support Vector)。为了达到最好的分类效果,SVM算法的原理就是要找到一个分隔超平面,它能把数据集正确地分类,并且间距最大。
首先,我们来看怎么计算间距。在二维空间里,可以使用方程w1x1+w2x2+b=0w_1x_1+w_2x_2+b=0w1x1+w2x2+b=0来表示分隔超平面。针对高维度空间,可以写成一般的向量化形式,即wTx+b=0w^Tx+b=0wTx+b=0。我们画出与分隔超平面平行的两条直线,分别穿过两个类别的支持向量(离分隔超平面距离最近的点)。这两条直线的方程分别为wTx+b=−1w^Tx+b=-1wTx+b=−1和wTx+b=1w^Tx+b=1wTx+b=1。如下图所示。
plt.figure(figsize=(8, 6), dpi=144)
plt.title('Support Vector Machine')
plt.xlim(0, 8)
plt.ylim(0, 6)
ax = plt.gca() # gca 代表当前坐标轴,即 'get current axis'
ax.spines['right'].set_color('none') # 隐藏坐标轴
ax.spines['top'].set_color('none')
plt.scatter(class1[:, 0], class1[:, 1], marker='o')
plt.scatter(class2[:, 0], class2[:, 1], marker='s')
plt.plot([1, 5], [5, 1], '-r')
plt.plot([0, 4], [4, 0], '--b', [2, 6], [6, 2], '--b')
plt.arrow(4, 4, -1, -1, shape='full', color='b')
plt.annotate(r'$w^T x + b = 0$',
xy=(5, 1), xycoords='data',
xytext=(6, 1), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$w^T x + b = 1$',
xy=(6, 2), xycoords='data',
xytext=(7, 2), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$w^T x + b = -1$',
xy=(3.5, 0.5), xycoords='data',
xytext=(4.5, 0.2), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'd',
xy=(3.5, 3.5), xycoords='data',
xytext=(2, 4.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'A',
xy=(4, 4), xycoords='data',
xytext=(5, 4.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
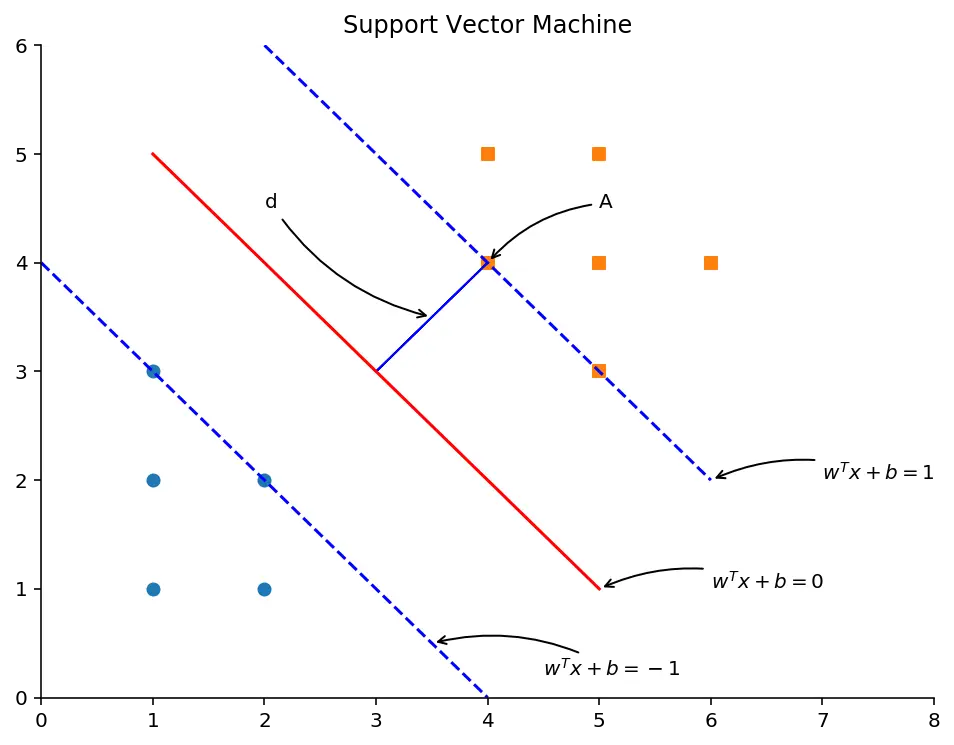
根据点到直线的距离公式,可以容易地算出支持向量A到分隔超平面的距离为:
d=∣wTA+b∣∣∣w∣∣d=\frac{|w^TA+b|}{||w||}d=∣∣w∣∣∣wTA+b∣
由于点A在直线wTx+b=1w^Tx+b=1wTx+b=1上,因此wTA+b=1w^TA+b=1wTA+b=1,代入即可算出支持向量A到分隔超平面的距离为d=1∣∣w∣∣d=\frac{1}{||w||}d=∣∣w∣∣1。为了使得距离最大,我们只需要找到合适的参数w和b,使得1∣∣w∣∣\frac{1}{||w||}∣∣w∣∣1最大即可。∣∣w∣∣||w||∣∣w∣∣是向量w的L2范数,其计算公式为:
∣∣w∣∣=∑i=1nwi2||w||=\sqrt{\sum_{i=1}^{n}w_i^2}∣∣w∣∣=i=1∑nwi2
由此可得,求1∣∣w∣∣\frac{1}{||w||}∣∣w∣∣1的最大值,等价于求∣∣w∣∣2||w||^2∣∣w∣∣2的最小值:
∣∣w∣∣2=∑i=1nwi2||w||^2=\sum_{i=1}^{n}w_i^2∣∣w∣∣2=i=1∑nwi2
其中n为向量w的维度。除了间距最大外,我们选出来的分隔超平面还要能正确地把数据集分类。问题来了,怎样在数学上表达出“正确地把数据集分类”这个描述呢?
根据上图可以看出,针对方形的点,必定满足wTx+b≥1w^Tx+b\geq1wTx+b≥1的约束条件。类别是离散的值,我们使用-1来表示圆形的类别,用1来表示方形的类别,即y∈{
−1,1}y \in \left\{-1,1\right\}y∈{
−1,1}。针对数据集中的所有样本x(i)x^{(i)}x(i),y(i)y^{(i)}y(i),只要它们都满足以下的约束条件,则由w和b定义的分隔超平面即可正确地把数据集分类:
y(i)(wTx(i)+b)≥1y^{(i)}(w^Tx^{(i)}+b)\geq1y(i)(wTx(i)+b)≥1
等等,怎么得出这个数学表达式的呢?
其技巧在于使用1和-1来定义类别标签。针对y(i)=1y^{(i)}=1y(i)=1的情况,由于其满足wTx(i)+b≥1w^Tx^{(i)}+b\geq1wTx(i)+b≥1的约束,两边都乘以y(i)y^{(i)}y(i)后,大于等于号保持不变。针对y(i)=−1y^{(i)}=-1y(i)=−1的情况,由于其满足wTx(i)+b≤−1w^Tx^{(i)}+b\leq-1wTx(i)+b≤−1的约束,两边都乘以y(i)y^{(i)}y(i)后,负负得正,小于等于号变成了大于等于号。这样,我们就可以使用一个公式来表达针对两个不同类别的约束函数了。
在逻辑回归算法里,使用0和1作为类别标签,而这里我们使用-1和1作为类别标签。其目的都是为了让数学表达尽量简洁。
总结:求解SVM算法,就是在满足约束条件y(i)(wTx(i)+b)≥1y^{(i)}(w^Tx^{(i)}+b)\geq1y(i)(wTx(i)+b)≥1的前提下,求解∣∣w∣∣2||w||^2∣∣w∣∣2的最小值。
2.松弛系数
针对线性不可分的数据集,上面介绍的方法就失灵了。因为无法找到最大间距的分隔超平面,如下图左所示。
from sklearn.datasets import make_blobs
plt.figure(figsize=(13, 6), dpi=144)
# sub plot 1
plt.subplot(1, 2, 1)
X, y = make_blobs(n_samples=100,
n_features=2,
centers=[(1, 1), (2, 2)],
random_state=4,
shuffle=False,
cluster_std=0.4)
plt.title('Non-linear Separatable')
plt.xlim(0, 3)
plt.ylim(0, 3)
ax = plt.gca() # gca 代表当前坐标轴,即 'get current axis'
ax.spines['right'].set_color('none') # 隐藏坐标轴
ax.spines['top'].set_color('none')
plt.scatter(X[y==0][:, 0], X[y==0][:, 1], marker='o')
plt.scatter(X[y==1][:, 0], X[y==1][:, 1], marker='s')
plt.plot([0.5, 2.5], [2.5, 0.5], '-r')
# sub plot 2
plt.subplot(1, 2, 2)
class1 = np.array([[1, 1], [1, 3], [2, 1], [1, 2], [2, 2], [1.5, 1.5], [1.2, 1.7]])
class2 = np.array([[4, 4], [5, 5], [5, 4], [5, 3], [4, 5], [6, 4], [5.5, 3.5], [4.5, 4.5], [2, 1.5]])
plt.title('Slack Variable')
plt.xlim(0, 7)
plt.ylim(0, 7)
ax = plt.gca() # gca 代表当前坐标轴,即 'get current axis'
ax.spines['right'].set_color('none') # 隐藏坐标轴
ax.spines['top'].set_color('none')
plt.scatter(class1[:, 0], class1[:, 1], marker='o')
plt.scatter(class2[:, 0], class2[:, 1], marker='s')
plt.plot([1, 5], [5, 1], '-r')
plt.plot([0, 4], [4, 0], '--b', [2, 6], [6, 2], '--b')
plt.arrow(2, 1.5, 2.25, 2.25, shape='full', color='b')
plt.annotate(r'violate margin rule.',
xy=(2, 1.5), xycoords='data',
xytext=(0.2, 0.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'normal sample. $\epsilon = 0$',
xy=(4, 5), xycoords='data',
xytext=(4.5, 5.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$\epsilon > 0$',
xy=(3, 2.5), xycoords='data',
xytext=(3, 1.5), fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
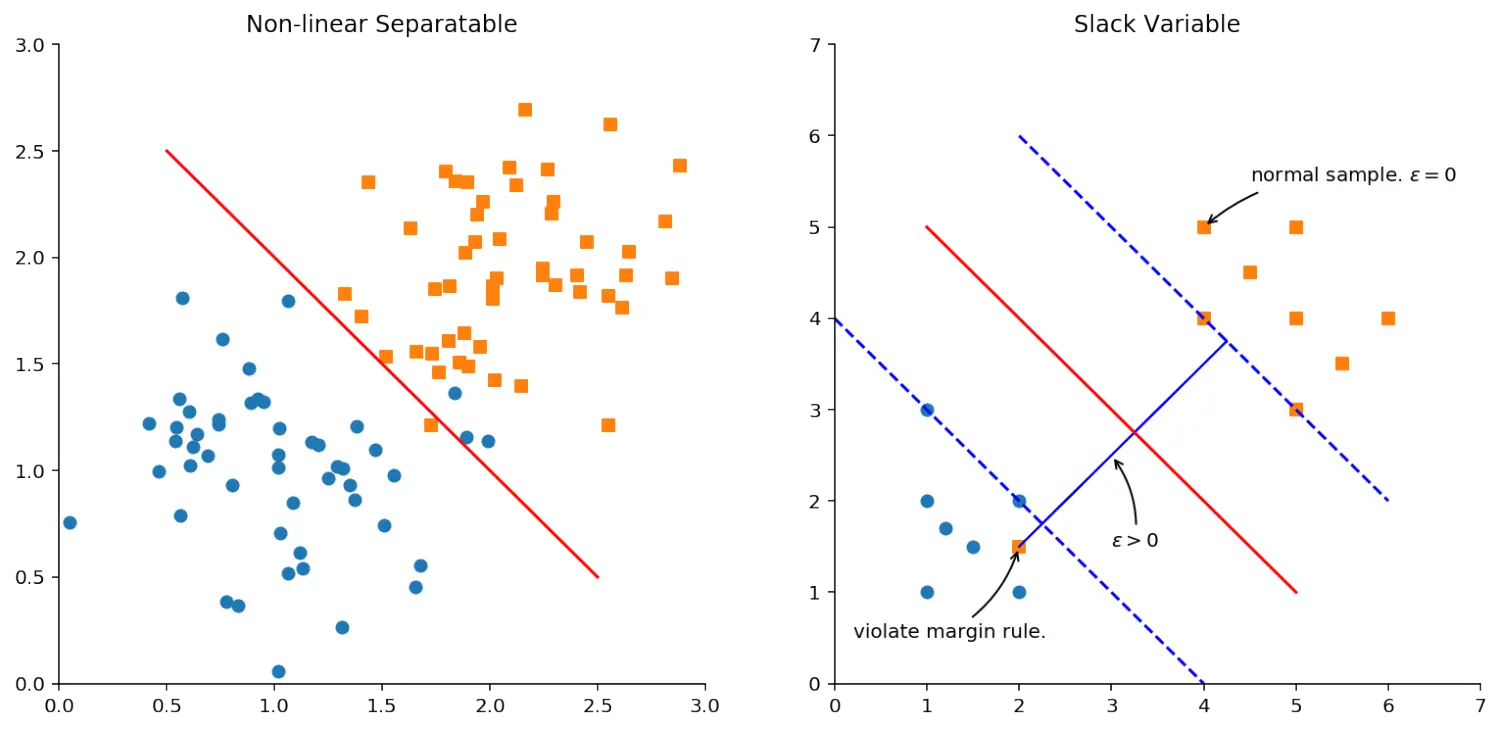
解决这个问题的办法是引入一个参数ε\varepsilonε,称为松弛系数。然后把优化的目标函数变为:
argmin∣∣w∣∣2+R∑i=1mεiargmin||w||^2+R\sum_{i=1}^{m}\varepsilon_iar
 支持向量机算法原理、核函数及应用示例
支持向量机算法原理、核函数及应用示例





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3232
3232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








