概率密度函数和概率分布函数的基本概念:
随机变量是指在任何时间点上,值都是不能完全确定的,最多只能知道它可能落在哪个区间上,那么怎样去描述这个变量呢?只能通过概率。概率密度函数(Probability Density Function, PDF)和概率分布函数(又称累积分布函数, Cumulative Distribution Function, CDF)分别从两个不同的角度来描述随机变量的概率。在说明PDF和CDF之前,首先来看一个统计问题,对于一组随机数,通常可以利用直方图来表示这组随机数在各个区间上的分布情况,如下图所示为随机生成100000个高斯分布的样本

P ( x 1 < x ≤ x 2 ) = ∫ x 1 x 2 f ( x ) d x (1) P(x_1 < x \leq x_2)=\int_{x_1}^{x_2} {f(x)dx} \tag{1} P(x1<x≤x2)=∫x1x2f(x)dx(1)
显然
f
(
x
)
≥
0
f(x) \geq 0
f(x)≥0,且
∫
x
1
x
2
f
(
x
)
d
x
=
1
\int_{x_1}^{x_2} {f(x)dx}=1
∫x1x2f(x)dx=1,为了从数学上更好地表示
(
1
)
(1)
(1),我们定义了CDF,其定义方式如下:
F
(
x
)
=
P
(
X
≤
x
)
(2)
F(x)=P(X \leq x) \tag{2}
F(x)=P(X≤x)(2)
从 ( 1 ) (1) (1)可以看出 F ( x ) F(x) F(x)暗含着概率累积的概念,这也就是它为什么又叫做累积分布函数的原因,这通过离散型随机变量的例子可以很容易理解,比如随机变量 X X X的取值是 0 ∽ 5 0 \backsim 5 0∽5的整数,则 F ( 3 ) = P ( X ≤ 3 ) = P ( 0 ) + P ( 1 ) + P ( 2 ) + P ( 3 ) F(3)=P(X \leq 3)=P(0)+P(1)+P(2)+P(3) F(3)=P(X≤3)=P(0)+P(1)+P(2)+P(3)。对比 ( 1 ) ( 2 ) (1)(2) (1)(2)两式可得
P
(
x
1
<
x
≤
x
2
)
=
F
(
x
2
)
−
F
(
x
1
)
=
∫
x
1
x
2
f
(
x
)
d
x
(3)
P(x_1 < x \leq x_2)=F(x_2)-F(x_1)=\int_{x_1}^{x_2} {f(x)dx} \tag{3}
P(x1<x≤x2)=F(x2)−F(x1)=∫x1x2f(x)dx(3)
(
3
)
(3)
(3)给出了PDF和CDF之间的关系,除此之外,它们还有如下一些常用的性质:
- F ( x ) F(x) F(x)是一个不减函数,即 F ( x 2 ) − F ( x 1 ) = P ( x 1 < x ≤ x 2 ) ≥ 0 F(x_2)-F(x_1)=P(x_1 < x \leq x_2) \geq 0 F(x2)−F(x1)=P(x1<x≤x2)≥0,其中 x 1 < x 2 x_1 < x_2 x1<x2;
- 0 ≤ F ( x ) ≤ 1 0 \leq F(x) \leq 1 0≤F(x)≤1,且 F ( − ∞ ) = lim x → − ∞ F ( x ) = P ( X < − ∞ ) = 0 F(-\infty)=\lim_{x \to -\infty}{F(x)}=P(X < -\infty)=0 F(−∞)=limx→−∞F(x)=P(X<−∞)=0, F ( ∞ ) = lim x → ∞ F ( x ) = P ( X < ∞ ) = 1 F(\infty)=\lim_{x \to \infty}{F(x)}=P(X < \infty)=1 F(∞)=limx→∞F(x)=P(X<∞)=1;
- F ( x ) = ∫ − ∞ x f ( t ) d t F(x)=\int_{-\infty}^x{f(t)dt} F(x)=∫−∞xf(t)dt, F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x)。
显然,当知道一个随机变量的PDF或CDF之后,该随机变量就能被很好描述了,所以确定随机变量的PDF或CDF是随机变量处理中的非常重要的一个内容。
PDF和CDF的更详细的信息,可以参考相关资料,比如《概率分布函数、概率密度函数》
上面讨论的都是一个随机变量的情况,在实际情况中经常需要考虑多个随机变量,下面以二维随机变量为例进行简单的说明。设 X X X, Y Y Y为两个随机变量,显然它们各自都有对应的PDF和CDF,分别记为 f X ( x ) , F X ( x ) f_X(x),F_X(x) fX(x),FX(x)和 f Y ( y ) , F Y ( y ) f_Y(y),F_Y(y) fY(y),FY(y),同时这两个随机变量还共同组成一个PDF和CDF,记为 f X Y ( x , y ) , F X Y ( x , y ) f_{XY}(x,y),F_{XY}(x,y) fXY(x,y),FXY(x,y),则上面各个变量之间存在如下一些常用的基本的关系:
- F X Y ( x , y ) = P ( X ≤ x , Y ≤ y ) = ∫ − ∞ y ∫ − ∞ x f ( μ , υ ) d μ d υ F_{XY}(x,y)=P(X \leq x,Y \leq y)=\int_{-\infty}^y{\int_{-\infty}^x{f(\mu,\upsilon)d\mu d\upsilon}} FXY(x,y)=P(X≤x,Y≤y)=∫−∞y∫−∞xf(μ,υ)dμdυ, F X Y ( − ∞ , ∞ ) = ∫ − ∞ ∞ ∫ − ∞ ∞ f ( x , y ) d x d y = 1 F_{XY}(-\infty,\infty)=\int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(x,y)dx dy}}=1 FXY(−∞,∞)=∫−∞∞∫−∞∞f(x,y)dxdy=1;
- f X Y ( x , y ) = ∂ 2 F X Y ( x , y ) ∂ x ∂ y f_{XY}(x,y)=\frac{\partial^2 F_{XY}(x,y)}{\partial x \partial y} fXY(x,y)=∂x∂y∂2FXY(x,y)
- F X ( x ) = F X Y ( x , ∞ ) , F Y ( y ) = F X Y ( ∞ , y ) , f X ( x ) = ∫ − ∞ ∞ f X Y ( x , y ) d y , f Y ( y ) = ∫ − ∞ ∞ f X Y ( x , y ) d x F_X(x)=F_{XY}(x,\infty),F_Y(y)=F_{XY}(\infty,y),f_X(x)=\int_{-\infty}^{\infty}{f_{XY}(x,y)dy},f_Y(y)=\int_{-\infty}^{\infty}{f_{XY}(x,y)dx} FX(x)=FXY(x,∞),FY(y)=FXY(∞,y),fX(x)=∫−∞∞fXY(x,y)dy,fY(y)=∫−∞∞fXY(x,y)dx
需要注意的是各随机变量之间可能是相关的,也就是彼此可能相互影响,所以综合的PDF和CDF不仅与每个随机变量各自的PDF和CDF有关,还和它们彼此之间的相关性有关。考虑一种最简单的情况,即当所有随机变量互相独立时,此时可以得到以下常用的结论:
- P ( X ≤ x , Y ≤ y ) = P ( X ≤ x ) P ( Y ≤ y ) , F X Y ( x , y ) = F X ( x ) F Y ( y ) , f X Y ( x , y ) = f X ( x ) f Y ( y ) P(X \leq x,Y \leq y)=P(X \leq x)P(Y \leq y),F_{XY}(x,y)=F_X(x)F_Y(y),f_{XY}(x,y)=f_X(x)f_Y(y) P(X≤x,Y≤y)=P(X≤x)P(Y≤y),FXY(x,y)=FX(x)FY(y),fXY(x,y)=fX(x)fY(y)
更多多维随机变量相关内容可以查阅资料,如《多维随机变量》
随机变量函数的概率密度函数和概率分布函数:
在实际应用中往往关注的不是某个随机变量的分布特征,而是这个随机变量某个函数的分布特征,比如在对复随机信号进行处理时,我们往往并不会关注它的实部、虚部分别满足什么样的分布,而是更希望了解它的幅度或功率的分布情况。因此需要探究如何根据已知随机变量的分布情况,求它的某个函数的分布情况,首先来考虑单个随机变量的情况,设随机变量
X
X
X的PDF和CDF分别为
f
X
(
x
)
,
F
X
(
x
)
f_X(x),F_X(x)
fX(x),FX(x),
Y
=
g
(
X
)
Y=g(X)
Y=g(X)为随机变量
X
X
X的一个函数,现在需要求解
Y
Y
Y的分布规律。求解方法如下:
F
Y
(
y
)
=
P
(
Y
≤
y
)
=
P
(
g
(
X
)
≤
y
)
=
P
(
X
≤
h
(
y
)
)
=
F
X
(
h
(
y
)
)
f
Y
(
y
)
=
F
Y
′
(
y
)
=
f
X
(
h
(
y
)
)
h
′
(
y
)
(4)
\begin{equation} \begin{aligned} F_Y(y)&=P(Y \leq y)=P(g(X) \leq y)=P(X \leq h(y))=F_X(h(y))\\ f_Y(y)&=F_Y'(y)=f_X(h(y))h'(y) \end{aligned} \end{equation}\tag{4}
FY(y)fY(y)=P(Y≤y)=P(g(X)≤y)=P(X≤h(y))=FX(h(y))=FY′(y)=fX(h(y))h′(y)(4)
上面的式子仅展示了一个基本的求解思路,并不严谨,基本的思路就是利用函数表达式
Y
=
g
(
X
)
Y=g(X)
Y=g(X),将
X
X
X表示为
Y
Y
Y的函数,即
X
=
h
(
Y
)
X=h(Y)
X=h(Y),这样就能利用
X
X
X的分布情况来求
Y
Y
Y的分布情况,以下给出更严谨的定理:
设随机变量
X
X
X具有PDF
f
X
(
x
)
,
−
∞
<
x
<
∞
f_X(x),-\infty < x < \infty
fX(x),−∞<x<∞,又设函数
g
(
x
)
g(x)
g(x)处处可导且恒有
g
′
(
x
)
>
0
g'(x)>0
g′(x)>0(或恒有
g
′
(
x
)
<
0
g'(x)< 0
g′(x)<0),则
Y
=
g
(
X
)
Y=g(X)
Y=g(X)是连续型随机变量,其概率密度函数为
f
Y
(
y
)
=
{
f
X
[
h
(
y
)
]
∣
h
′
(
y
)
∣
,
α
<
y
<
β
0
,
other
(5)
f_Y(y)= \begin{cases} f_X[h(y)]|h'(y)|, & \text {$\alpha < y < \beta$} \\ 0, & \text{other} \end{cases} \tag{5}
fY(y)={fX[h(y)]∣h′(y)∣,0,α<y<βother(5)
其中
α
=
m
i
n
[
g
(
−
∞
)
,
g
(
∞
)
]
,
β
=
m
a
x
[
g
(
−
∞
)
,
g
(
∞
)
]
\alpha=min[g(-\infty),g(\infty)],\beta=max[g(-\infty),g(\infty)]
α=min[g(−∞),g(∞)],β=max[g(−∞),g(∞)],
h
(
y
)
h(y)
h(y)是
g
(
x
)
g(x)
g(x)的反函数。
上面给出了单个随机变量的函数的PDF求解方法,对于多个随机变量函数的PDF,可以按照类似的思路进行处理,但是因为涉及到多个变量,显然求解的过程会复杂很多,一般也没有一个通用的表达式,通常也只需要根据实际情况进行具体的求解,以下通过两个随机变量函数的PDF求解来展示一下基本的过程:
(1)
Z
=
X
+
Y
Z=X+Y
Z=X+Y的分布
F
Z
(
z
)
=
P
(
Z
≤
z
)
=
P
(
X
+
Y
≤
z
)
=
∬
x
+
y
≤
z
f
X
Y
(
x
,
y
)
d
x
d
y
=
∫
−
∞
∞
[
∫
−
∞
z
−
y
f
X
Y
(
z
−
y
,
y
)
d
x
]
d
y
→
μ
=
x
+
y
F
Z
(
z
)
=
∫
−
∞
∞
[
∫
−
∞
z
f
X
Y
(
μ
−
y
,
y
)
d
μ
]
d
y
=
∫
−
∞
z
[
∫
−
∞
∞
f
X
Y
(
μ
−
y
,
y
)
d
y
]
d
μ
\begin{equation} \begin{aligned} F_Z(z)&=P(Z \leq z)=P(X+Y \leq z)=\iint_{x+y \leq z} f_{XY}(x,y)\,dx\,dy=\int_{-\infty}^{\infty}{[\int_{-\infty}^{z-y}{f_{XY}(z-y,y)dx}]dy} \\ \stackrel{\mu=x+y}{\rightarrow} F_Z(z)&=\int_{-\infty}^{\infty}{[\int_{-\infty}^{z}{f_{XY}(\mu-y,y)d\mu}]dy}=\int_{-\infty}^{z}{[\int_{-\infty}^{\infty}{f_{XY}(\mu-y,y)dy}]d\mu} \end{aligned} \end{equation}
FZ(z)→μ=x+yFZ(z)=P(Z≤z)=P(X+Y≤z)=∬x+y≤zfXY(x,y)dxdy=∫−∞∞[∫−∞z−yfXY(z−y,y)dx]dy=∫−∞∞[∫−∞zfXY(μ−y,y)dμ]dy=∫−∞z[∫−∞∞fXY(μ−y,y)dy]dμ
所以
f
Z
(
z
)
=
∫
−
∞
∞
f
X
Y
(
z
−
y
,
y
)
d
y
f_Z(z)=\int_{-\infty}^{\infty}{f_{XY}(z-y,y)dy}
fZ(z)=∫−∞∞fXY(z−y,y)dy,由于
x
,
y
x,y
x,y在上面的式子中是完全对称的,所以显然有
f
Z
(
z
)
=
∫
−
∞
∞
f
X
Y
(
x
,
z
−
x
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{f_{XY}(x,z-x)dx}
fZ(z)=∫−∞∞fXY(x,z−x)dx,当
X
,
Y
X,Y
X,Y相互独立时,
f
X
Y
(
x
,
y
)
=
f
X
(
x
)
f
Y
(
y
)
f_{XY}(x,y)=f_X(x)f_Y(y)
fXY(x,y)=fX(x)fY(y),所以此时
f
Z
(
z
)
=
∫
−
∞
∞
f
X
(
z
−
y
)
f
Y
(
y
)
d
y
f_Z(z)=\int_{-\infty}^{\infty}{f_X(z-y)f_Y(y)dy}
fZ(z)=∫−∞∞fX(z−y)fY(y)dy或
f
Z
(
z
)
=
∫
−
∞
∞
f
X
(
x
)
f
Y
(
z
−
x
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{f_X(x)f_Y(z-x)dx}
fZ(z)=∫−∞∞fX(x)fY(z−x)dx,可以看出此时随机变量
Z
Z
Z的PDF是随机变量
X
,
Y
X,Y
X,Y的PDF的卷积。
由于两个高斯函数的卷积仍然为高斯函数,因此根据上面的结论可得,两个服从高斯分布的相互独立的随机变量的和仍然服从高斯分布,更具体地:
设
X
X
X,
Y
Y
Y相互独立且
X
∽
N
(
μ
x
,
σ
x
2
)
X \backsim N(\mu_x,\sigma_x^2)
X∽N(μx,σx2),
Y
∽
N
(
μ
y
,
σ
y
2
)
Y \backsim N(\mu_y,\sigma_y^2)
Y∽N(μy,σy2),则
Z
=
X
+
Y
Z=X+Y
Z=X+Y仍然服从高斯分布,且
Z
∽
N
(
μ
x
+
μ
y
,
σ
x
2
+
σ
y
2
)
Z \backsim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)
Z∽N(μx+μy,σx2+σy2)。进一步地,有限个相互独立的正态随机变量的线性组合仍然服从正态分布,且若
X
i
∽
N
(
μ
i
,
σ
i
2
)
,
i
=
1
,
2
,
.
.
.
,
n
X_i \backsim N(\mu_i,\sigma_i^2),i=1,2,...,n
Xi∽N(μi,σi2),i=1,2,...,n,
Z
=
∑
i
=
1
n
k
i
X
i
Z=\sum_{i=1}^n{k_i X_i}
Z=∑i=1nkiXi,则
Z
∽
N
(
∑
i
=
1
n
k
i
μ
i
,
∑
i
=
1
n
k
i
2
σ
i
2
)
Z \backsim N(\sum_{i=1}^n{k_i \mu_i},\sum_{i=1}^n{k_i^2 \sigma_i^2})
Z∽N(∑i=1nkiμi,∑i=1nki2σi2)
(2)
Z
=
Y
/
X
Z=Y/X
Z=Y/X的分布
F
Z
(
z
)
=
P
(
Z
≤
z
)
=
P
(
Y
/
X
≤
z
)
=
∬
y
/
x
≤
z
,
x
>
0
f
X
Y
(
x
,
y
)
d
x
d
y
+
∬
y
/
x
≤
z
,
x
<
0
f
X
Y
(
x
,
y
)
d
x
d
y
=
∫
0
∞
[
∫
x
z
∞
f
X
Y
(
x
,
y
)
d
y
]
d
x
+
∫
−
∞
0
[
∫
−
∞
x
z
f
X
Y
(
x
,
y
)
d
y
]
d
x
→
y
=
x
μ
F
Z
(
z
)
=
∫
0
∞
[
∫
−
∞
z
x
f
X
Y
(
x
,
x
μ
)
d
μ
]
d
x
+
∫
−
∞
0
[
∫
z
∞
x
f
X
Y
(
x
,
x
μ
)
d
μ
]
d
x
=
∫
−
∞
∞
[
∫
−
∞
z
∣
x
∣
f
X
Y
(
x
,
x
μ
)
d
μ
]
d
x
=
∫
−
∞
z
[
∫
−
∞
∞
∣
x
∣
f
X
Y
(
x
,
x
μ
)
d
x
]
d
μ
\begin{equation} \begin{aligned} F_Z(z)&=P(Z \leq z)=P(Y/X \leq z)=\iint_{y/x \leq z,x > 0} f_{XY}(x,y)\,dx\,dy+\iint_{y/x \leq z,x < 0} f_{XY}(x,y)\,dx\,dy \\ &=\int_0^{\infty}{[\int_{xz}^{\infty}{f_{XY}(x,y)dy}]}dx+\int_{-\infty}^0{[\int_{-\infty}^{xz}{f_{XY}(x,y)dy}]}dx \\ &\stackrel{y=x\mu}{\rightarrow} F_Z(z)=\int_0^{\infty}{[\int_{-\infty}^{z}{xf_{XY}(x,x\mu)d\mu}]}dx+\int_{-\infty}^0{[\int_{z}^{\infty}{xf_{XY}(x,x\mu)d\mu}]}dx \\ &= \int_{-\infty}^{\infty}{[\int_{-\infty}^{z}{|x|f_{XY}(x,x\mu)d\mu}]}dx=\int_{-\infty}^z{[\int_{-\infty}^{\infty}{|x|f_{XY}(x,x\mu)dx}]}d\mu \end{aligned} \end{equation}
FZ(z)=P(Z≤z)=P(Y/X≤z)=∬y/x≤z,x>0fXY(x,y)dxdy+∬y/x≤z,x<0fXY(x,y)dxdy=∫0∞[∫xz∞fXY(x,y)dy]dx+∫−∞0[∫−∞xzfXY(x,y)dy]dx→y=xμFZ(z)=∫0∞[∫−∞zxfXY(x,xμ)dμ]dx+∫−∞0[∫z∞xfXY(x,xμ)dμ]dx=∫−∞∞[∫−∞z∣x∣fXY(x,xμ)dμ]dx=∫−∞z[∫−∞∞∣x∣fXY(x,xμ)dx]dμ
所以
f
Z
(
z
)
=
∫
−
∞
∞
∣
x
∣
f
X
Y
(
x
,
x
z
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{|x|f_{XY}(x,xz)dx}
fZ(z)=∫−∞∞∣x∣fXY(x,xz)dx,当
X
,
Y
X,Y
X,Y相互独立时,
f
X
Y
(
x
,
y
)
=
f
X
(
x
)
f
Y
(
y
)
f_{XY}(x,y)=f_X(x)f_Y(y)
fXY(x,y)=fX(x)fY(y),所以此时
f
Z
(
z
)
=
∫
−
∞
∞
∣
x
∣
f
X
(
x
)
f
Y
(
x
z
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{|x|f_X(x)f_Y(xz)dx}
fZ(z)=∫−∞∞∣x∣fX(x)fY(xz)dx。
(3)
Z
=
X
Y
Z=XY
Z=XY的分布
F
Z
(
z
)
=
P
(
Z
≤
z
)
=
P
(
X
Y
≤
z
)
=
∬
x
y
≤
z
,
x
>
0
f
X
Y
(
x
,
y
)
d
x
d
y
+
∬
x
y
≤
z
,
x
<
0
f
X
Y
(
x
,
y
)
d
x
d
y
=
∫
0
∞
[
∫
−
∞
z
/
x
f
X
Y
(
x
,
y
)
d
y
]
d
x
+
∫
−
∞
0
[
∫
z
/
x
∞
f
X
Y
(
x
,
y
)
d
y
]
d
x
→
y
=
μ
/
x
F
Z
(
z
)
=
∫
0
∞
[
∫
−
∞
z
1
x
f
X
Y
(
x
,
μ
/
x
)
d
μ
]
d
x
+
∫
−
∞
0
[
∫
−
∞
z
−
1
x
f
X
Y
(
x
,
μ
/
x
)
d
μ
]
d
x
=
∫
−
∞
z
[
∫
−
∞
∞
1
∣
x
∣
f
X
Y
(
x
,
μ
/
x
)
d
x
]
d
μ
\begin{equation} \begin{aligned} F_Z(z)&=P(Z \leq z)=P(XY \leq z)=\iint_{xy \leq z,x > 0} f_{XY}(x,y)\,dx\,dy+\iint_{xy \leq z,x < 0} f_{XY}(x,y)\,dx\,dy \\ &=\int_0^{\infty}{[\int_{-\infty}^{z/x}{f_{XY}(x,y)dy}]}dx+\int_{-\infty}^0{[\int_{z/x}^{\infty}{f_{XY}(x,y)dy}]}dx \\ &\stackrel{y=\mu/x}{\rightarrow} F_Z(z)=\int_0^{\infty}{[\int_{-\infty}^{z}{\frac{1}{x}f_{XY}(x,\mu/x)d\mu]}dx}+\int_{-\infty}^0{[\int_{-\infty}^{z}{-\frac{1}{x}f_{XY}(x,\mu/x)d\mu]}dx} \\ &= \int_{-\infty}^z{[\int_{-\infty}^{\infty}{\frac{1}{|x|}f_{XY}(x,\mu/x)dx]}d\mu} \end{aligned} \end{equation}
FZ(z)=P(Z≤z)=P(XY≤z)=∬xy≤z,x>0fXY(x,y)dxdy+∬xy≤z,x<0fXY(x,y)dxdy=∫0∞[∫−∞z/xfXY(x,y)dy]dx+∫−∞0[∫z/x∞fXY(x,y)dy]dx→y=μ/xFZ(z)=∫0∞[∫−∞zx1fXY(x,μ/x)dμ]dx+∫−∞0[∫−∞z−x1fXY(x,μ/x)dμ]dx=∫−∞z[∫−∞∞∣x∣1fXY(x,μ/x)dx]dμ
所以
f
Z
(
z
)
=
∫
−
∞
∞
1
∣
x
∣
f
X
Y
(
x
,
z
/
x
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{\frac{1}{|x|}f_{XY}(x,z/x)dx}
fZ(z)=∫−∞∞∣x∣1fXY(x,z/x)dx,当
X
,
Y
X,Y
X,Y相互独立时,
f
X
Y
(
x
,
y
)
=
f
X
(
x
)
f
Y
(
y
)
f_{XY}(x,y)=f_X(x)f_Y(y)
fXY(x,y)=fX(x)fY(y),所以此时
f
Z
(
z
)
=
∫
−
∞
∞
1
∣
x
∣
f
X
(
x
)
f
Y
(
z
/
x
)
d
x
f_Z(z)=\int_{-\infty}^{\infty}{\frac{1}{|x|}f_X(x)f_Y(z/x)dx}
fZ(z)=∫−∞∞∣x∣1fX(x)fY(z/x)dx。
除了上述常见的随机变量函数的分布以外,复随机信号的分布也是在实际问题中经常会遇到的内容,以下来推导几个与复随机信号相关的常见的分布。
1.设 X ∽ N ( μ x , σ x 2 ) X \backsim N(\mu_x,\sigma_x^2) X∽N(μx,σx2), Y ∽ N ( μ y , σ y 2 ) Y \backsim N(\mu_y,\sigma_y^2) Y∽N(μy,σy2),且两者相互独立, Z = X + i Y Z=X+iY Z=X+iY,显然根据上面1)的结论可知, Z Z Z也服从高斯分布,此时 Z Z Z的PDF可以参考《正态分布》
2.设
X
∽
N
(
0
,
σ
2
)
X \backsim N(0,\sigma^2)
X∽N(0,σ2),
Y
∽
N
(
0
,
σ
2
)
Y \backsim N(0,\sigma^2)
Y∽N(0,σ2),且两者相互独立,则
Z
=
X
2
+
Y
2
Z=X^2+Y^2
Z=X2+Y2服从指数分布,其PDF可通过下面的方法进行求解:
f
X
(
x
)
=
1
2
π
σ
e
x
p
(
−
x
2
2
σ
2
)
f
Y
(
y
)
=
1
2
π
σ
e
x
p
(
−
y
2
2
σ
2
)
,
→
f
X
Y
(
x
,
y
)
=
f
X
(
x
)
f
Y
(
y
)
=
1
2
π
σ
2
e
x
p
(
−
x
2
+
y
2
2
σ
2
)
F
Z
(
z
)
=
P
(
Z
≤
z
)
=
P
(
X
2
+
Y
2
≤
z
)
=
∬
x
2
+
y
2
≤
z
f
X
Y
(
x
,
y
)
d
x
d
y
=
∫
0
2
π
[
∫
0
z
f
X
Y
(
ρ
c
o
s
θ
,
ρ
s
i
n
θ
)
ρ
d
ρ
]
d
θ
=
1
2
π
σ
2
∫
0
2
π
[
∫
0
z
e
x
p
(
−
ρ
2
2
σ
2
)
ρ
d
ρ
]
d
θ
=
1
2
π
σ
2
∫
0
2
π
d
θ
∫
0
z
e
x
p
(
−
ρ
2
2
σ
2
)
d
ρ
2
=
1
−
e
x
p
(
−
z
2
σ
2
)
\begin{equation} \begin{aligned} f_X(x)&=\frac{1}{\sqrt{2\pi}\sigma}{\rm exp}(-\frac{x^2}{2\sigma^2})\\ f_Y(y)&=\frac{1}{\sqrt{2\pi}\sigma}{\rm exp}(-\frac{y^2}{2\sigma^2}),\rightarrow f_{XY}(x,y)=f_X(x)f_Y(y)=\frac{1}{2\pi\sigma^2}{\rm exp}(-\frac{x^2+y^2}{2\sigma^2})\\ F_Z(z)&=P(Z \leq z)=P(X^2+Y^2 \leq z)=\iint_{x^2+y^2 \leq z} f_{XY}(x,y)\,dx\,dy=\int_0^{2\pi}{[\int_0^{\sqrt{z}}{f_{XY}(\rho cos\theta,\rho sin\theta)\rho d\rho}]d\theta} \\ &=\frac{1}{2\pi\sigma^2}\int_0^{2\pi}{[\int_0^{\sqrt{z}}{{\rm exp}(-\frac{\rho^2}{2\sigma^2})\rho d\rho}]d\theta}=\frac{1}{2\pi\sigma^2}\int_0^{2\pi}{d\theta}\int_0^{\sqrt{z}}{{\rm exp}(-\frac{\rho^2}{2\sigma^2})d\rho^2}=1-{\rm exp}(-\frac{z}{2\sigma^2}) \end{aligned} \end{equation}
fX(x)fY(y)FZ(z)=2πσ1exp(−2σ2x2)=2πσ1exp(−2σ2y2),→fXY(x,y)=fX(x)fY(y)=2πσ21exp(−2σ2x2+y2)=P(Z≤z)=P(X2+Y2≤z)=∬x2+y2≤zfXY(x,y)dxdy=∫02π[∫0zfXY(ρcosθ,ρsinθ)ρdρ]dθ=2πσ21∫02π[∫0zexp(−2σ2ρ2)ρdρ]dθ=2πσ21∫02πdθ∫0zexp(−2σ2ρ2)dρ2=1−exp(−2σ2z)
所以
f
Z
(
z
)
=
F
Z
′
(
z
)
=
1
2
σ
2
e
x
p
(
−
z
2
σ
2
)
f_Z(z)=F_Z^{'}(z)=\frac{1}{2\sigma^2}{\rm exp}(-\frac{z}{2\sigma^2})
fZ(z)=FZ′(z)=2σ21exp(−2σ2z)。
3.设
X
∽
N
(
0
,
σ
2
)
X \backsim N(0,\sigma^2)
X∽N(0,σ2),
Y
∽
N
(
0
,
σ
2
)
Y \backsim N(0,\sigma^2)
Y∽N(0,σ2),且两者相互独立,则
Z
=
X
2
+
Y
2
Z=\sqrt{X^2+Y^2}
Z=X2+Y2服从瑞利分布,其PDF可通过下面的方法进行求解:
f
X
(
x
)
=
1
2
π
σ
e
x
p
(
−
x
2
2
σ
2
)
f
Y
(
y
)
=
1
2
π
σ
e
x
p
(
−
y
2
2
σ
2
)
,
→
f
X
Y
(
x
,
y
)
=
f
X
(
x
)
f
Y
(
y
)
=
1
2
π
σ
2
e
x
p
(
−
x
2
+
y
2
2
σ
2
)
F
Z
(
z
)
=
P
(
Z
≤
z
)
=
P
(
X
2
+
Y
2
≤
z
)
=
∬
x
2
+
y
2
≤
z
f
X
Y
(
x
,
y
)
d
x
d
y
=
∫
0
2
π
[
∫
0
z
f
X
Y
(
ρ
c
o
s
θ
,
ρ
s
i
n
θ
)
ρ
d
ρ
]
d
θ
=
1
2
π
σ
2
∫
0
2
π
[
∫
0
z
e
x
p
(
−
ρ
2
2
σ
2
)
ρ
d
ρ
]
d
θ
=
1
2
π
σ
2
∫
0
2
π
d
θ
∫
0
z
e
x
p
(
−
ρ
2
2
σ
2
)
d
ρ
2
=
1
−
e
x
p
(
−
z
2
2
σ
2
)
\begin{equation} \begin{aligned} f_X(x)&=\frac{1}{\sqrt{2\pi}\sigma}{\rm exp}(-\frac{x^2}{2\sigma^2})\\ f_Y(y)&=\frac{1}{\sqrt{2\pi}\sigma}{\rm exp}(-\frac{y^2}{2\sigma^2}),\rightarrow f_{XY}(x,y)=f_X(x)f_Y(y)=\frac{1}{2\pi\sigma^2}{\rm exp}(-\frac{x^2+y^2}{2\sigma^2})\\ F_Z(z)&=P(Z \leq z)=P(\sqrt{X^2+Y^2} \leq z)=\iint_{\sqrt{x^2+y^2} \leq z} f_{XY}(x,y)\,dx\,dy=\int_0^{2\pi}{[\int_0^z{f_{XY}(\rho cos\theta,\rho sin\theta)\rho d\rho}]d\theta} \\ &=\frac{1}{2\pi\sigma^2}\int_0^{2\pi}{[\int_0^z{{\rm exp}(-\frac{\rho^2}{2\sigma^2})\rho d\rho}]d\theta}=\frac{1}{2\pi\sigma^2}\int_0^{2\pi}{d\theta}\int_0^z{{\rm exp}(-\frac{\rho^2}{2\sigma^2})d\rho^2}=1-{\rm exp}(-\frac{z^2}{2\sigma^2}) \end{aligned} \end{equation}
fX(x)fY(y)FZ(z)=2πσ1exp(−2σ2x2)=2πσ1exp(−2σ2y2),→fXY(x,y)=fX(x)fY(y)=2πσ21exp(−2σ2x2+y2)=P(Z≤z)=P(X2+Y2≤z)=∬x2+y2≤zfXY(x,y)dxdy=∫02π[∫0zfXY(ρcosθ,ρsinθ)ρdρ]dθ=2πσ21∫02π[∫0zexp(−2σ2ρ2)ρdρ]dθ=2πσ21∫02πdθ∫0zexp(−2σ2ρ2)dρ2=1−exp(−2σ2z2)
所以 f Z ( z ) = F Z ′ ( z ) = z σ 2 e x p ( − z 2 2 σ 2 ) f_Z(z)=F_Z^{'}(z)=\frac{z}{\sigma^2}{\rm exp}(-\frac{z^2}{2\sigma^2}) fZ(z)=FZ′(z)=σ2zexp(−2σ2z2)
下面对上述复高斯变量的幅度和功率的分布进行仿真验证,仿真代码如下:
mu=0;sigma=4; %高斯分布的均值和方差
x=sigma*randn(100000,1)+mu; %实部的值
y=4*randn(100000,1)+mu; %虚部的值
z1=sqrt(x.^2+y.^2); %模值
z2=x.^2+y.^2; %功率值
s=-20:0.1:20;
x_=exp(-(s-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));%理论高斯分布概率密度函数
y_=exp(-(s-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));%理论高斯分布概率密度函数
s1=0:0.1:20;
z1_=s1/sigma^2.*exp(-s1.^2/(2*sigma^2)); %理论瑞利分布概率密度函数
s2=0:0.1:400;
z2_=1/(2*sigma^2).*exp(-s2/(2*sigma^2)); %理论指数分布概率密度函数
histogram(x,'Normalization','pdf','NumBins',40);
hold on;
plot(s,x_,'LineWidth',1.5);xlabel('实部样本值');ylabel('概率');axis tight;
figure;
histogram(y,'Normalization','pdf','NumBins',40);
hold on;
plot(s,y_,'LineWidth',1.5);xlabel('实部样本值');ylabel('概率');axis tight;
figure;
histogram(z1,'Normalization','pdf','NumBins',40);
hold on;
plot(s1,z1_,'LineWidth',1.5);xlabel('幅值');ylabel('概率');axis tight;
figure;
histogram(z2,'Normalization','pdf','NumBins',40);
hold on;
plot(s2,z2_,'LineWidth',1.5);xlabel('功率值');ylabel('概率');axis tight;
运行结果如下:



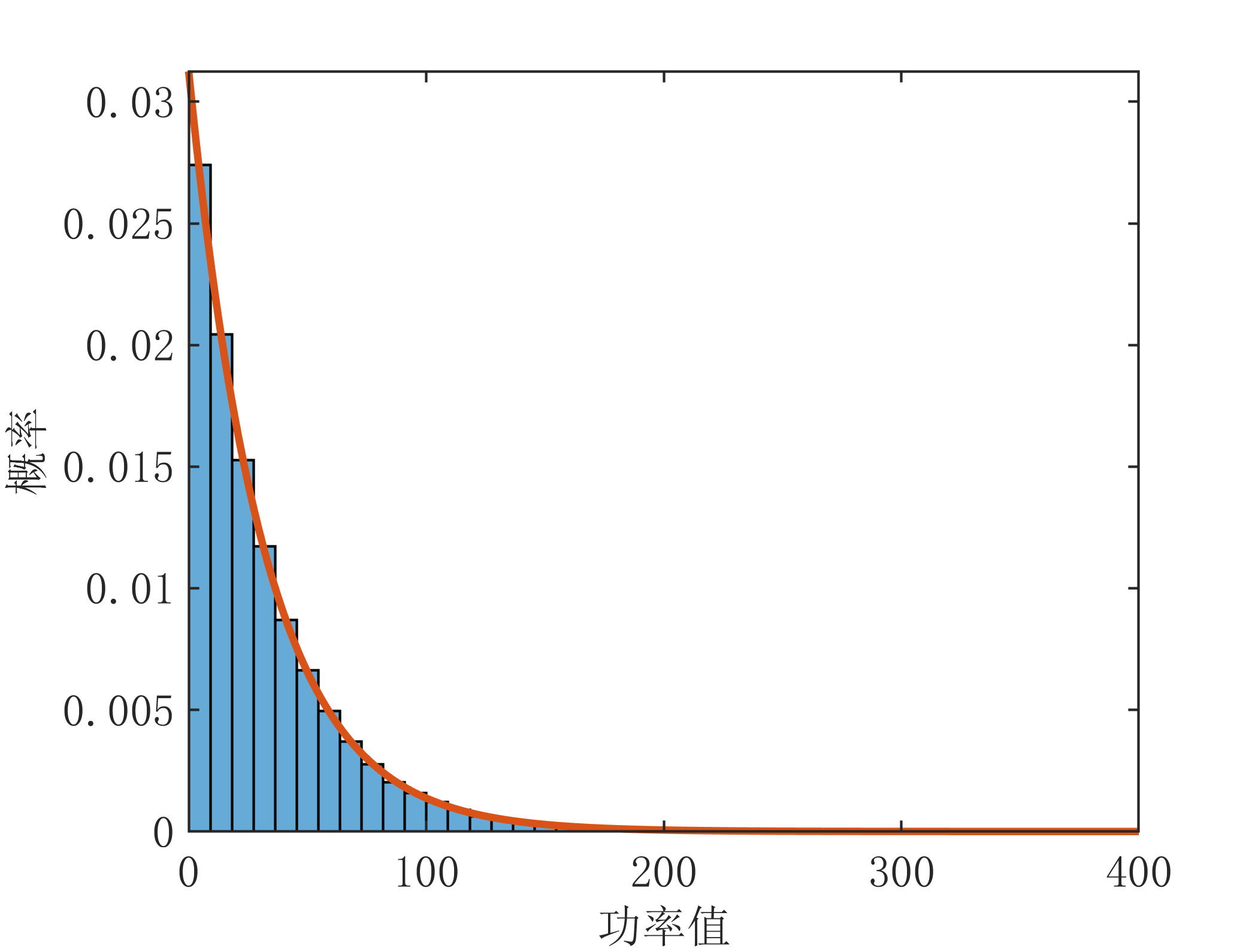
随机样本 X X X的常用统计分布:
(1)正态分布
其概率密度函数可以表示为:
X
∽
N
(
μ
,
σ
2
)
:
f
(
x
)
=
1
2
π
σ
2
e
x
p
[
−
(
x
−
μ
)
2
2
σ
2
]
(6)
X \backsim N(\mu,\sigma^2):f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}{\rm exp}[\frac{-(x-\mu)^2}{2\sigma^2}] \tag{6}
X∽N(μ,σ2):f(x)=2πσ21exp[2σ2−(x−μ)2](6)
其中
μ
\mu
μ,
σ
2
\sigma^2
σ2分别表示均值和方差,当
μ
=
0
\mu=0
μ=0,
σ
2
=
1
\sigma^2=1
σ2=1时,服从标准正态分布,其概率密度函数可以表示为:
X
∽
N
(
0
,
1
)
:
f
(
x
)
=
1
2
π
e
x
p
(
−
x
2
2
)
(7)
X \backsim N(0,1):f(x)=\frac{1}{\sqrt{2\pi}}{\rm exp}(\frac{-x^2}{2}) \tag{7}
X∽N(0,1):f(x)=2π1exp(2−x2)(7)




关于上述分布的其他信息可以参考数理统计四大分布—正态分布、卡方分布、学生t分布和F分布






















 1942
1942











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








