均匀背景下常用恒虚警检测推导及比较(一)：理论推导部分

均匀背景下常用恒虚警检测推导及比较

本文档对均匀背景下常用恒虚警检测算法，包括CA-CFAR，OS-CFAR，GO-CFAR，SO-CFAR进行简单的分析和比较，具体地，推导了每种算法的虚警概率、检测概率的表达式，并简单地比较了它们在均匀背景中的性能。

一、理论最优性能

本文均是对高斯噪声背景下的单样本平方率检波进行分析的。此时待检单元$x$在$H_0$和$H_1$两种检验假设条件下的概率密度函数可以分别表示为
$$\begin{array}{c}\begin{array}{rl}& f(x|H_0)={\lambda }_0{e}^{-{\lambda }_{0}x},x\ge 0\\ & f(x|H_1)={\lambda }_1{e}^{-{\lambda }_{1}x},x\ge 0\end{array}\end{array}\text{\hspace{1em}(1)}$$
其中${\lambda }_0=\frac{1}{{\sigma }^2}$​​，${\lambda }_1=\frac{1}{{\sigma }^2(1+\mathrm{SNR})}$​​，且${\sigma }^2$​​表示待检单元的噪声功率值，$\mathrm{SNR}$​​表示目标的信噪比。由此可以求得理论虚警概率$P_{FA}$​​和检测概率$P_D$​​分别为
$$\begin{array}{c}\begin{array}{rl}& P_{FA}={\int }_T^{\infty }f(x|H_0)dx=e^{-{\lambda }_{0}T}=e^{-T/{\sigma }^2}\\ & P_D={\int }_T^{\infty }f(x|H_1)dx=e^{-{\lambda }_{1}T}=e^{-T/[{\sigma }^2(1+\mathrm{SNR})]}\end{array}\end{array}\text{\hspace{1em}(2)}$$
其中$T$​​表示门限值，可以看出理论虚警概率和检测概率均与噪声功率值和设置的门限有关。且$P_D=P_{FA}^{1/(1+\mathrm{SNR})}$​​。

二、CFAR算法的统一推导思路

(1)中推导了已知噪声功率条件下的理论虚警概率和检测概率。在实际应用中噪声功率是没办法作为先验知识精确已知的，而是需要从实测数据中进行估计。CFAR算法就是利用待检单元周围的单元(称为参考窗)得到噪声功率估计值${\hat{\sigma }}^2$，然后自适应设置检测门限$T=\alpha {\hat{\sigma }}^2$，从而使得检测虚警率保持恒定。不同类型的CFAR算法的差别就在于${\hat{\sigma }}^2$获取方法上的差异。设$x_i$表示第$i$个参考窗单元，则理想情况下我们希望参考窗各个单元中只包含噪声成分，即其服从$f_{x_i}(x_i)={\lambda }_0{e}^{-{\lambda }_0{x}_i}$的指数分布。不同CFAR算法利用$x_i$的方式有差异，设$z$表示CFAR算法估计的噪声功率${\hat{\sigma }}^2$，则对于不同类型CFAR，$z$的表达式分别为：
$$\begin{array}{c}\begin{array}{rl}& \mathrm{CA}-\mathrm{CFAR}:z=\frac{1}{N}\sum _{i=1}^N{x}_i\\ & \mathrm{GO}-\mathrm{CFAR}:z=\max (\frac{2}{N}\sum _{i=1}^{N/2}{x}_i,\frac{2}{N}\sum _{i=N/2+1}^N{x}_i)\\ & \mathrm{SO}-\mathrm{CFAR}:z=\min (\frac{2}{N}\sum _{i=1}^{N/2}{x}_i,\frac{2}{N}\sum _{i=N/2+1}^N{x}_i)\\ & \mathrm{OS}-\mathrm{CFAR}:z=x_{(k)}\end{array}\end{array}\text{\hspace{1em}(3)}$$
显然可以由$x_i$的概率密度函数求得噪声功率的概率密度函数$f_z(z)$，然后可以进一步地利用$\hat{T}=\alpha {\hat{\sigma }}^2=\alpha z$求得检测门限的概率密度函数$f_{\hat{T}}(\hat{T})$。由于$P_{FA}$和$P_D$是检测门限$T$的函数，而$T$的估计值$\hat{T}$是满足一定分布的随机变量，所以通常采用$P_{FA}$和$P_D$的期望值${\overline{P}}_{FA}$和${\overline{P}}_D$来表征CFAR算法的性能。${\overline{P}}_{FA}$和${\overline{P}}_D$的计算通常有以下两种方法：
$$\begin{array}{c}\begin{array}{rl}{\overline{P}}_{FA}& =\mathrm{E}[{\int }_{\hat{T}}^{\infty }f(x|H_0)dx]=\mathrm{E}[e^{-{\lambda }_0\hat{T}}]=\mathrm{E}[e^{-{\lambda }_0\alpha z}]={\mathrm{M}}_z(\alpha {\lambda }_0)\\ {\overline{P}}_D& =\mathrm{E}[{\int }_{\hat{T}}^{\infty }f(x|H_1)dx]=\mathrm{E}[e^{-{\lambda }_1\hat{T}}]=\mathrm{E}[e^{-{\lambda }_1\alpha z}]={\mathrm{M}}_z(\alpha {\lambda }_1)\\ {\overline{P}}_{FA}& ={\int }_0^{\infty }{e}^{-{\lambda }_0\hat{T}}{f}_{\hat{T}}(\hat{T})d\hat{T}\\ {\overline{P}}_D& ={\int }_0^{\infty }{e}^{-{\lambda }_1\hat{T}}{f}_{\hat{T}}(\hat{T})d\hat{T}\end{array}\end{array}\text{\hspace{1em}(4)}$$
在上面的表达式中$M_z$表示变量$z$的矩母函数，其相关内容可以参考文献[2]。上面两种做法虽然是等价的，但是可以从两种不同的物理含义进行理解。第一种方法直接利用了$P_{FA}$和$P_D$的定义，即虚警概率表示当目标不存在时，待检单元超过设定门限值的概率；检测概率表示当目标存在时，待检单元超过设定门限的概率，所以第一种方法直接将待检单元作为操作对象。第二种方法利用的是随机变量函数的期望计算方法，它的积分对象是门限值$T$。

从上面的说明我们知道CFAR算法的噪声功率是从参考窗中估计得到的，为了获取CFAR门限$\hat{T}=\alpha {\hat{\sigma }}^2$，还需要求得门限乘积因子$\alpha$，通常从(4)中我们可以得到${\overline{P}}_{FA}$和$\alpha$的函数关系，继而可以反推得到$\alpha$值。以此完成整个CFAR算法的实现过程。

三、 CA-CFAR

由(3)可知CA-CFAR将参考单元的平均噪声作为待检单元的噪声估计值，显然这是对待检单元噪声的极大似然估计，当参考单元长度$N\to +\infty$时，该估计结果趋近于真实噪声值。

由参考单元$x_i$的概率密度函数及(3)中所示噪声估计值$z$的表达式，所以$z$的概率密度函数可以表示为(具体推导过程参考附录1)
$$Z\backsim \mathrm{G}(N,N{\lambda }_0):f_z(z)=\frac{(N{\lambda }_0{)}^N}{\Gamma (N)}{z}^{N-1}{e}^{-N{\lambda }_{0}z}\text{\hspace{1em}(5)}$$
由于$\hat{T}=\alpha z$，所以可以求得$\hat{T}$的概率密度函数为
$$\hat{T}\backsim \mathrm{G}(N,N{\lambda }_0/\alpha ):f_{\hat{T}}(\hat{T})=\frac{(N{\lambda }_0/\alpha {)}^N}{\Gamma (N)}{\hat{T}}^{N-1}{e}^{-N{\lambda }_0\hat{T}/\alpha }\text{\hspace{1em}(6)}$$
由(4)可得
$$\begin{array}{c}\begin{array}{rl}{\overline{P}}_{FA}& ={\mathrm{M}}_z(\alpha {\lambda }_0)={\int }_0^{\infty }{e}^{-{\lambda }_0\hat{T}}{f}_{\hat{T}}(\hat{T})d\hat{T}\\ {\overline{P}}_D& ={\mathrm{M}}_z(\alpha {\lambda }_1)={\int }_0^{\infty }{e}^{-{\lambda }_1\hat{T}}{f}_{\hat{T}}(\hat{T})d\hat{T}\end{array}\end{array}\text{\hspace{1em}(7)}$$
利用结论：$x\backsim \mathrm{G}(n,\lambda )\to {\mathrm{M}}_x(t)=(1+\frac{t}{\lambda }{)}^{-n}$​​，具体推导过程可以参考附录2或文献[3]。可以得到${\mathrm{M}}_z(t)=(1+\frac{t}{N{\lambda }_0}{)}^{-N}$​​，所以${\mathrm{M}}_z(\alpha {\lambda }_0)=(1+\frac{\alpha }{N}{)}^{-N}$​​，${\mathrm{M}}_z(\alpha {\lambda }_1)=[1+\frac{\alpha }{N(1+\mathrm{SNR})}{]}^{-N}$​​，所以${\overline{P}}_{FA}=(1+\frac{\alpha }{N}{)}^{-N}$​​，${\overline{P}}_D=[1+\frac{\alpha }{N(1+\mathrm{SNR})}{]}^{-N}$​​。需要注意(7)中${\overline{P}}_{FA}$​​和${\overline{P}}_D$​​中第二个等号右边式子的推导过程，完全可以借鉴Gamma分布矩母函数的推导过程进行求解。可以看出${\overline{P}}_{FA}$​​与噪声功率无关，因此具有恒虚警特性。且可以反推得到$\alpha =N({\overline{P}}_{FA}^{-1/N}-1)$​​，据此可以完整实现CA-CFAR。

四、GO-CFAR

GO-CFAR选择前、后参考窗中平均噪声较大的那个作为噪声估计值，设$Z_1=\frac{2}{N}{\sum }_{i=1}^{N/2}{X}_i$表示前参考窗噪声估计结果，$Z_2=\frac{2}{N}{\sum }_{i=N/2+1}^N{X}_i$表示后参考窗噪声估计结果，则GO-CFAR最终噪声估计结果为$Z=\max (Z_1,Z_2)$，参考(3)中的分析和推导过程我们可以得到$Z_1\backsim \mathrm{G}(N/2,N{\lambda }_0/2),Z_2\backsim \mathrm{G}(N/2,N{\lambda }_0/2)$，而随机变量$Z$的概率密度函数可以表示为$f_z(z)=f_{z_1}(z)F_{z_2}(z)+f_{z_2}(z)F_{z_1}(z)$，其中$F_{z_1}(z_1),F_{z_2}(z_2)$分别表示随机变量$Z_1,Z_2$的概率分布函数，由附录(4)可知
$$\begin{array}{c}\begin{array}{rl}{F}_{z_1}(z_1)& =1-e^{-N{\lambda }_0{z}_1/2}\sum _{k=0}^{N/2-1}\frac{(N{\lambda }_0{z}_1/2{)}^k}{k!}\\ F_{z_2}(z_2)& =1-e^{-N{\lambda }_0{z}_2/2}\sum _{k=0}^{N/2-1}\frac{(N{\lambda }_0{z}_2/2{)}^k}{k!}\end{array}\end{array}\text{\hspace{1em}(8)}$$
所以
$$f_z(z)=2\frac{(N{\lambda }_0/2{)}^{N/2}}{\Gamma (N/2)}{z}^{N/2-1}{e}^{-N{\lambda }_{0}z/2}[1-e^{-N{\lambda }_{0}z/2}\sum _{k=0}^{N/2-1}\frac{(N{\lambda }_{0}z/2{)}^k}{k!}]\text{\hspace{1em}(9)}$$
利用(2)可以求得$z$的矩母函数为(具体求解过程可以参考附录(5))
$${\mathrm{M}}_z(t)=2(n{\lambda }_0{)}^n(n{\lambda }_0+t{)}^{-n}-2(n{\lambda }_0{)}^n\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(n{\lambda }_0{)}^k(2n{\lambda }_0+t{)}^{-(n+k)}\text{\hspace{1em}(10)}$$
在上面的表达式中$n=N/2$，所以由(4)可得
$$\begin{array}{c}\begin{array}{rl}{\overline{P}}_{FA}& ={\mathrm{M}}_z(\alpha {\lambda }_0)=2(1+\frac{\alpha }{n}{)}^{-n}-2\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(2+\frac{\alpha }{n}{)}^{-(n+k)}\\ {\overline{P}}_D& ={\mathrm{M}}_z(\alpha {\lambda }_1)=2[1+\frac{\alpha }{n(1+\mathrm{SNR})}{]}^{-n}-2\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)[2+\frac{\alpha }{n(1+\mathrm{SNR})}{]}^{-(n+k)}\end{array}\end{array}\text{\hspace{1em}(11)}$$

从(11)可以看出虚警概率与噪声功率无关，因此GO-CFAR具有恒虚警特性。虽然(11)推导出了GO-CFAR的虚警概率和检测概率的表达式，但是由于表达式太复杂，门限乘积因子$\alpha$的求解相对比较困难，在实际应用过程中通常有两种求解思路：一是从GO-CFAR算法的原理分析，它与CA-CFAR具有很多相似的地方，因此可以借由CA-CFAR门限乘积因子的表达式来求解，将其中与参考单元数$N$换成$N/2$即可。二是用迭代法直接对(11)式进行求解，比如二分法、最陡下降法、牛顿下降法等。

五、SO-CFAR

SO-CFAR和GO-CFAR的差别在于SO-CFAR选择前后参考窗中噪声较小的值作为噪声估计结果，所以此时噪声估计量$Z=\min (Z_1,Z_2)$，所以随机变量$Z$的概率密度函数可以表示为$f_z(z)=f_{z_1}(z)+f_{z_2}(z)-[f_{z_1}(z)F_{z_2}(z)+f_{z_2}(z)F_{z_1}(z)]$，所以$z$的矩母函数可以很方便地求得(可以利用GO-CFAR中矩母函数的计算结果)
$${\mathrm{M}}_z(t)=2(1+\frac{t}{n{\lambda }_0}{)}^{-n}-[2(n{\lambda }_0{)}^n(n{\lambda }_0+t{)}^{-n}-2(n{\lambda }_0{)}^n\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(n{\lambda }_0{)}^k(2n{\lambda }_0+t{)}^{-(n+k)}]\text{\hspace{1em}(12)}$$
所以
$$\begin{array}{c}\begin{array}{rl}{\overline{P}}_{FA}& ={\mathrm{M}}_z(\alpha {\lambda }_0)=2\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(2+\frac{\alpha }{n}{)}^{-(n+k)}\\ {\overline{P}}_D& ={\mathrm{M}}_z(\alpha {\lambda }_1)=2\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)[2+\frac{\alpha }{n(1+\mathrm{SNR})}{]}^{-(n+k)}\end{array}\end{array}\text{\hspace{1em}(13)}$$
可以看出虚警概率与噪声功率无关，所以SO-CFAR也具有恒虚警特性，其门限乘积因子的求解方法和GO-CFAR中类似。

六、OS-CFAR

上面介绍的CFAR算法均属于均值类CFAR，他们均是利用参考窗内的平均噪声作为估计噪声。而OS-CFAR属于有序统计的方法，它首先对参考窗进行排序，然后选择某一个参考窗内的值作为估计噪声。由附录(6)可知，估计噪声$z$的概率密度函数可以表示为
$$f_z(z)=\frac{N!}{(k-1)!(N-k)!}[F(z){]}^{k-1}[1-F(z){]}^{N-k}f(z)\text{\hspace{1em}(14)}$$
在上面的表达式中$f(z),F(z)$分别表示参考窗中各个单元的概率密度函数和分布函数，所以$f(z)={\lambda }_0{e}^{-{\lambda }_{0}z},F(z)=1-e^{-{\lambda }_{0}x}$，将其代入(14)可
$$f_z(z)={\lambda }_0\frac{N!}{(k-1)!(N-k)!}{e}^{-{\lambda }_0(N-k+1)z}[1-e^{-{\lambda }_{0}z}{]}^{k-1}\text{\hspace{1em}(15)}$$
据此可求$z$对应的矩母函数(具体过程参考附录(7))为
$${\mathrm{M}}_z(t)=k\left(\begin{array}{c}N\\ k\end{array}\right)\mathrm{B}(N-k+1+t/{\lambda }_0,k)\text{\hspace{1em}(16)}$$
所以其虚警概率和检测概率可以分别表示为
$$\begin{array}{c}\begin{array}{rl}{\overline{P}}_{FA}& ={\mathrm{M}}_z(\alpha {\lambda }_0)=k\left(\begin{array}{c}N\\ k\end{array}\right)\mathrm{B}(N-k+1+\alpha ,k)\\ {\overline{P}}_D& ={\mathrm{M}}_z(\alpha {\lambda }_1)=k\left(\begin{array}{c}N\\ k\end{array}\right)\mathrm{B}(N-k+1+\frac{\alpha }{1+\mathrm{SNR}},k)\end{array}\end{array}\text{\hspace{1em}(17)}$$
当$\alpha$为整数时，上面的式子可进一步化简为
$${\overline{P}}_{FA}=\frac{N!(N-k+\alpha )!}{(N-k)!(N+\alpha )!}\text{\hspace{1em}(18)}$$
显然OS-CFAR中虚警概率与噪声功率无关，所以OS-CFAR算法具有恒虚警特性。

七、上述各种算法性能对比

**比较一：**在相同虚警概率的条件下，比较各种算法的检测概率，检测概率越高，性能越好(具体代码参考附录(11))

图6 不同CFAR算法性能对比

如上图所示，在均匀噪声环境中CA-CFAR的性能最优，GO-CFAR相对于CA-CFAR存在较小的性能损失，OS-CFAR性能介于GO-CFAR和SO-CFAR之间，SO-CFAR的性能则最差。

**比较二：**仿真单目标情况下，各种算法门限设置情况(具体代码参考附录(12))

图7 单目标条件下不同算法的的门限设置情况

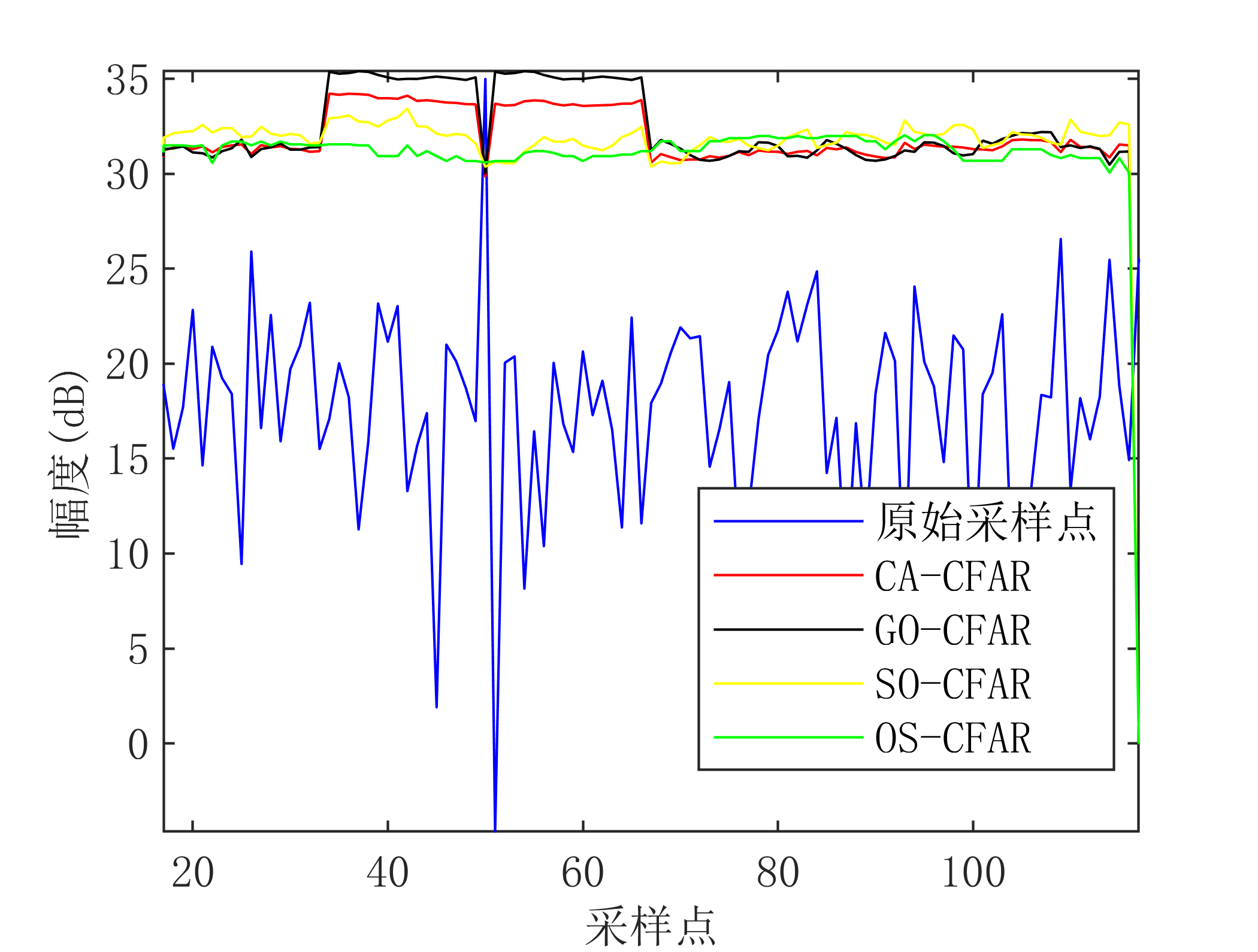
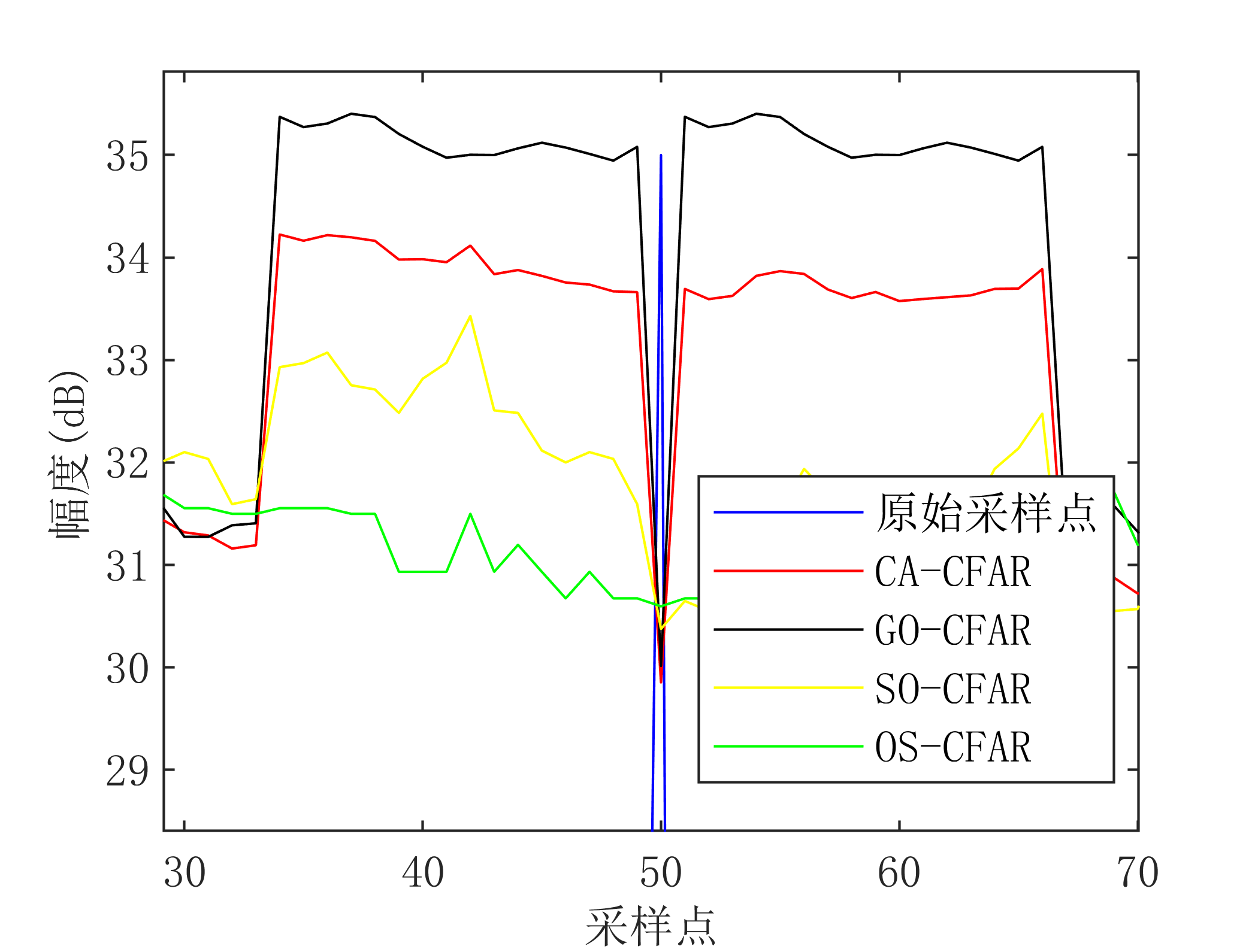
如上图所示，仿真单目标情况下各种CFAR算法的门限设置情况，其中噪声背景功率为20dB，目标信噪比为15dB，位于第50个距离单元上，可以看出对于CA-CFAR和GO-CFAR来说，目标两侧距离单元的检测门限明显高于其他单元，这是因为当待检单元位于目标两侧靠近目标的距离单元上时，目标能量被计算到了噪声背景中，导致检测门限急剧升高。而对于，SO-CFAR和OS-CFAR来说，目标能量对门限的影响较小。

比较三: 在单目标情况下，进行蒙特卡洛仿真验证检测概率的正确性(具体代码参考附录(13))

图8 各CFAR算法检测概率蒙特卡洛仿真结果

感觉上述结果还存在问题，因为理论检测概率和蒙特卡洛得到的概率之间的差异太大了，但是目前还没有发现哪个环节出现了问题，是理论检测概率计算错误了？还是仿真的原始信号出现错误？期望能在后续学习过程中找出其中的原因。

上面的问题已经找到原因了，问题出现在目标回波的生成方面，在附录(13)的代码里面，仿真目标是一种确定性信号，其实这是不对的，从第一节《理论最优性能》的分析过程中，我们知道其实目标所在单元和噪声一样，经平方率检波后都服从指数分布，只是两者对应的指数分布的参数不一样而已，所以在仿真目标回波的时候仍然需要将其当成随机变量来看待，而不应该将其仿真成一个确定性信号。修改之后的代码如附录(14)所示，其结果如图9所示：

图9 各CFAR算法检测概率蒙特卡洛仿真结果

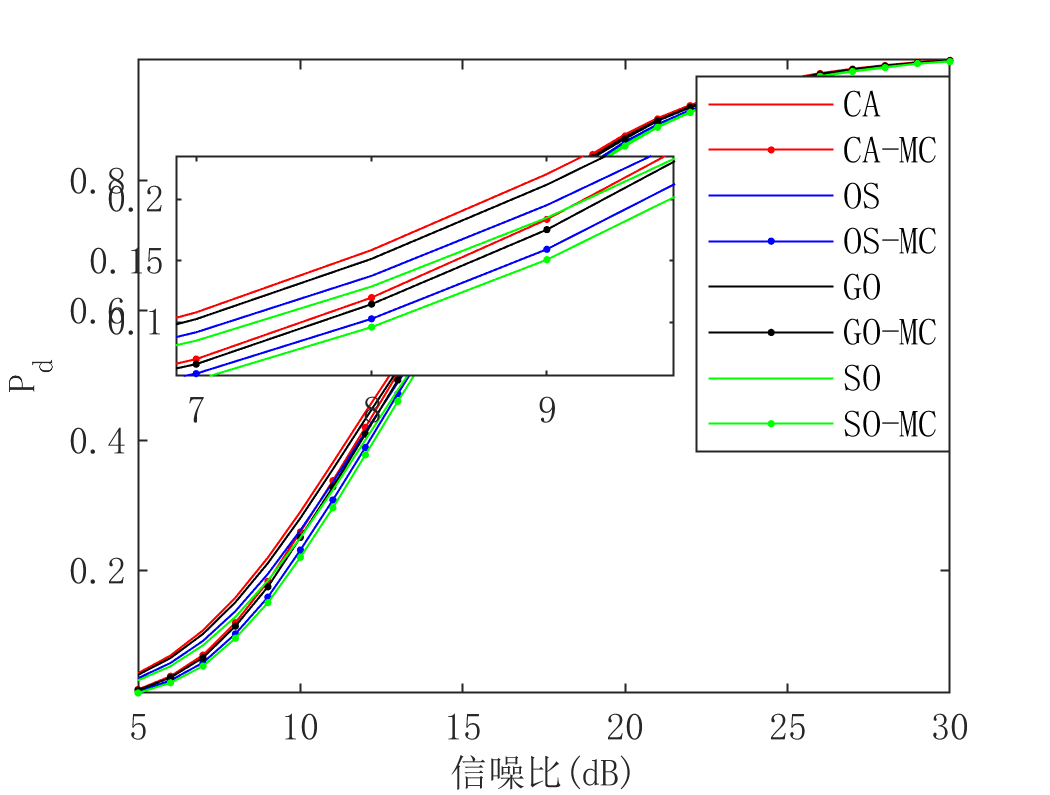
**比较四：文献[11]中定义了平均判决阈值(Average Detection Threshold, ADT)**用于评估不同CFAR之间的性能，它的定义如下：
$$\mathrm{ADT}=\frac{\mathrm{E}(\alpha Z)}{{\sigma }^2}={\lambda }_0\alpha \mathrm{E}(Z)={\lambda }_0\alpha {\int }_0^{\infty }zf(z)dz\text{\hspace{1em}(19)}$$
上式中期望可以用矩母函数表示，所以上式可以改写为
$$\mathrm{ADT}=-{\lambda }_0\alpha \frac{d{\mathrm{M}}_z(t)}{dt}{|}_{t=0}$$
在上式中，门限乘积因子$\alpha$由虚警概率决定，每个虚警概率对应特定的$\alpha$，所以$\mathrm{ADT}$表示的就是当虚警概率恒定时，各种CFAR算法设置的平均门限大小(相对于噪声归一化后的大小)，所以$\mathrm{ADT}$越小，表示门限值越低，所以此时检测概率越高，性能越好。根据上面的定义，及之前推导得到的各种CFAR算法对应的矩母函数${\mathrm{M}}_z(t)$，可以求得，上述CFAR算法对应的$\mathrm{ADT}$分别为：
$$\begin{array}{c}\begin{array}{rl}& \mathrm{CA}-\mathrm{CFAR}:\mathrm{ADT}=\alpha \\ & \mathrm{GO}-\mathrm{CFAR}:\mathrm{ADT}=-2\alpha +2\frac{\alpha }{n}\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(n+k)2^{-(n+k+1)}\\ & \mathrm{SO}-\mathrm{CFAR}:\mathrm{ADT}=4\alpha -2\frac{\alpha }{n}\sum _{k=0}^{n-1}\left(\begin{array}{c}n-1+k\\ k\end{array}\right)(n+k)2^{-(n+k+1)}\\ & \mathrm{OS}-\mathrm{CFAR}:\mathrm{ADT}=\frac{\alpha }{N}\sum _{i=1}^k\frac{1}{n-k+i}\end{array}\end{array}\text{\hspace{1em}(20)}$$

文章附录及代码验证见《均匀背景下常用恒虚警检测推导及比较(二)：附录+代码验证》

---

参考文献

[1] 常用恒虚警检测算法的推导过程

[2] 如何通俗地理解矩母函数

[3] 常用概率分布的矩母函数、特征函数以及期望、方差的推导

[4] Gamma分布常用笔记

[5] 不完全Gamma函数及各种相关表达式

[6]Ritcey J A , Hines J L . Performance of Max-Mean Level Detector With and Without Censoring[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2):213-223.

[7]Hansen V G , Sawyers J H . Detectability Loss Due to “Greatest Of” Selection in a Cell-Averaging CFAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, AES-16(1):115-118.

[8]Gandhi P P , Kassam S A . Analysis of CFAR processors in nonhomogeneous background[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 24(4):427-445.

[9] 数理统计第四讲(次序统计量续，伽马分布)

[10]Gradshteyn I S , Ryzhik I M . Table of Integrals, Series, and Products / I.S. Gradsheyn, I.M. Ryzhik ; ed. de Alan Jeffrey, Daniel Zwillinger.

[11]Rohling H . Radar CFAR Thresholding in Clutter and Multiple Target Situations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, 19(4):608-621.

---