Hilbert R树发展

Introduction

R-trees is one of the most efficient methods that support range queries(查询）

The most successful variant of R trees seems to be the R*-tree.

main contribution

• defer the splitting

• choosing some rectangles from the overflowing node, and “force-reinserting”

Hilbert　R-tree main idea

propose(提出) an ordering of the data rectangle
- Require:
- Each R-tree node has a well defined set of siblings(purpose:using the B*-tree algorithms for deferred splitting 可以达到类似B*树一样的对空间的高利用率)
- R*树对利用率没有过多的关心，平均利用率只达到了70%

使用了不规则的数据进行了实验->Static Hilbert R-trees/Dynamic Hilbert R-tree

在Hilbert R树之前的探索

Guttman proposed three splitting algorithms
1. linear split（线性分裂）
2. quadratic split（二次分裂）//能够最好的实现分裂时间和搜索效率的交换
3. exponential split（指数分裂）

Subsequent work on R-trees includes R+-tree,R-tree using Minimum Bounding Polygons(最小边界多边形）R*-tree.All above R-tree varients support insertions and deletions,are suitable for dynamic environments.

Roussopoulos and Leifker proposed a method
利用x，y 坐标实现R树近似100%的空间利用率，连续的矩形数据被分配到相同的叶结点中，直到这个叶结点满了，然后再创建新的叶结点。但是这个时间比R*树和二次分裂R树更差。

Static Version

• lowx packing method
  
  
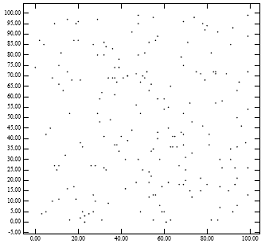
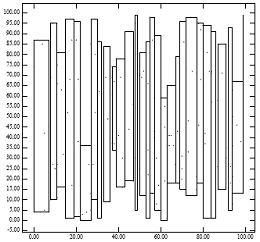
  忽略了y轴坐标，实际的实验中也证明得出的划分违反了统计学中的经验法则

• space filling curves

  1. Z-order
  2. Hilbert curve
  3. Gray-code curve

Purpose:使相近的点能够在一个划分中,使得R树的结点矩形能够占据更小的区域