R 树 空间索引 相关内容

///

什么是R树？

解析：

B树是一棵平衡树，它是把一维直线分为若干段线段，当我们查找满足某个要求的点的时候，只要去查找它所属的线段即可。依我看来，这种思想其实就是先找一个大的空间，再逐步缩小所要查找的空间，最终在一个自己设定的最小不可分空间内找出满足要求的解。

一个典型的B树查找如下：

要查找某一满足条件的点，先去找到满足条件的线段，然后遍历所在线段上的点，即可找到答案。

B树是一种相对来说比较复杂的数据结构，尤其是在它的删除与插入操作过程中，因为它涉及到了叶子结点的分解与合并。由于本文第一节已经详细介绍了B树和B+树，下面直接开始介绍我们的第二个主角：R树。

简介

1984年，加州大学伯克利分校的Guttman发表了一篇题为“R-trees: a dynamic index structure for spatial searching”的论文，向世人介绍了R树这种处理高维空间存储问题的数据结构。本文便是基于这篇论文写作完成的，因此如果大家对R树非常有兴趣，我想最好还是参考一下原著：）。为表示对这位牛人的尊重，给个引用先：

Guttman, A.; “R-trees: a dynamic index structure for spatial searching,” ACM, 1984, 14

R树在数据库等领域做出的功绩是非常显著的。它很好的解决了在高维空间搜索等问题。

举个R树在现实领域中能够解决的例子：查找20英里以内所有的餐厅。如果没有R树你会怎么解决？

一般情况下我们会把餐厅的坐标(x,y)分为两个字段存放在数据库中，一个字段记录经度，另一个字段记录纬度。这样的话我们就需要遍历所有的餐厅获取其位置信息，然后计算是否满足要求。

如果一个地区有100家餐厅的话，我们就要进行100次位置计算操作了，如果应用到谷歌地图这种超大数据库中，这种方法便必定不可行了。

R树就很好的解决了这种高维空间搜索问题。它把B树的思想很好的扩展到了多维空间，采用了B树分割空间的思想，并在添加、删除操作时采用合并、分解结点的方法，保证树的平衡性。因此，R树就是一棵用来存储高维数据的平衡树。

本文将详细介绍R树的数据结构以及R树的操作。至于R树的扩展与R树的性能问题，可以查阅相关论文。

R树的数据结构

如上所述，R树是B树在高维空间的扩展，是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。

根据R树的这种数据结构，当我们需要进行一个高维空间查询时，我们只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足要求即可。

这种方式使我们不必遍历所有数据即可获得答案，效率显著提高。下图1是R树的一个简单实例：

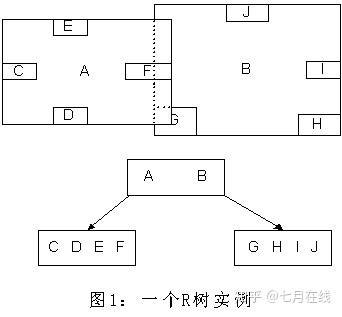
我们在上面说过，R树运用了空间分割的理念，这种理念是如何实现的呢？R树采用了一种称为MBR(Minimal Bounding Rectangle)的方法，在此我把它译作“最小边界矩形”。

从叶子结点开始用矩形（rectangle）将空间框起来，结点越往上，框住的空间就越大，以此对空间进行分割。

在这里我还想提一下，R树中的R应该代表的是Rectangle（此处参考wikipedia上关于R树的介绍），而不是大多数国内教材中所说的Region（很多书把R树称为区域树，这是有误的）。

我们就拿二维空间来举例。下图是Guttman论文中的一幅图：

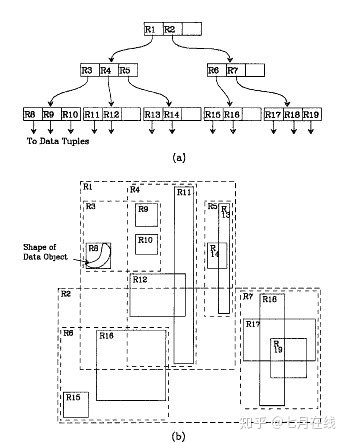
我来详细解释一下这张图。

先来看图（b）

A）首先我们假设所有数据都是二维空间下的点，图中仅仅标志了R8区域中的数据，也就是那个shape of data object。别把那一块不规则图形看成一个数据，我们把它看作是多个数据围成的一个区域。

为了实现R树结构，我们用一个最小边界矩形恰好框住这个不规则区域，这样，我们就构造出了一个区域：R8。R8的特点很明显，就是正正好好框住所有在此区域中的数据。其他实线包围住的区域，如R9，R10，R12等都是同样的道理。

这样一来，我们一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。

B）下一步操作就是进行高一层次的处理。我们发现R8，R9，R10三个矩形距离最为靠近，因此就可以用一个更大的矩形R3恰好框住这3个矩形。

C）同样道理，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。

我想大家都应该理解这个数据结构的特征了。用地图的例子来解释，就是所有的数据都是餐厅所对应的地点，先把相邻的餐厅划分到同一块区域，划分好所有餐厅之后，再把邻近的区域划分到更大的区域，划分完毕后再次进行更高层次的划分，直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。

下面就可以把这些大大小小的矩形存入我们的R树中去了。根结点存放的是两个最大的矩形，这两个最大的矩形框住了所有的剩余的矩形，当然也就框住了所有的数据。下一层的结点存放了次大的矩形，这些矩形缩小了范围。每个叶子结点都是存放的最小的矩形，这些矩形中可能包含有n个数据。

在这里，读者先不要去纠结于如何划分数据到最小区域矩形，也不要纠结怎样用更大的矩形框住小矩形，这些都是下一节我们要讨论的。

讲完了基本的数据结构，我们来讲个实例，如何查询特定的数据。又以餐厅为例，假设我要查询广州市天河区天河城附近一公里的所有餐厅地址怎么办？

1 打开地图（也就是整个R树），先选择国内还是国外（也就是根结点）。

2 然后选择华南地区（对应第一层结点），选择广州市（对应第二层结点），

3 再选择天河区（对应第三层结点），

4 最后选择天河城所在的那个区域（对应叶子结点，存放有最小矩形），遍历所有在此区域内的结点，看是否满足我们的要求即可。

怎么样，其实R树的查找规则跟查地图很像吧？对应下图：

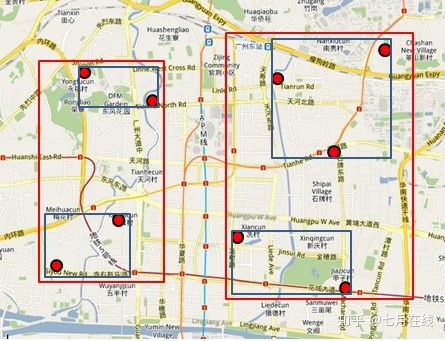
一棵R树满足如下的性质：

1. 除非它是根结点之外，所有叶子结点包含有m至M个记录索引（条目）。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。

2. 对于所有在叶子中存储的记录（条目），I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（注意：此处所说的“矩形”是可以扩展到高维空间的）。

3. 每一个非叶子结点拥有m至M个孩子结点，除非它是根结点。

4. 对于在非叶子结点上的每一个条目，i是最小的可以在空间上完全覆盖这些条目所代表的店的矩形（同性质2）。

5. 所有叶子结点都位于同一层，因此R树为平衡树。

叶子结点的结构

先来探究一下叶子结点的结构。叶子结点所保存的数据形式为：(I, tuple-identifier)。

其中，tuple-identifier表示的是一个存放于数据库中的tuple，也就是一条记录，它是n维的。I是一个n维空间的矩形，并可以恰好框住这个叶子结点中所有记录代表的n维空间中的点。I=(I0,I1,…,In-1)。其结构如下图所示：

下图描述的就是在二维空间中的叶子结点所要存储的信息。

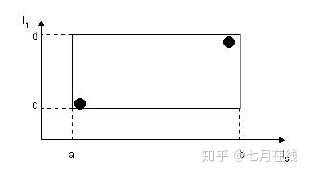
在这张图中，I所代表的就是图中的矩形，其范围是a<=I0<=b，c<=I1<=d。有两个tuple-identifier，在图中即表示为那两个点。这种形式完全可以推广到高维空间。大家简单想想三维空间中的样子就可以了。这样，叶子结点的结构就介绍完了。

非叶子结点

非叶子结点的结构其实与叶子结点非常类似。想象一下B树就知道了，B树的叶子结点存放的是真实存在的数据，而非叶子结点存放的是这些数据的“边界”，或者说也算是一种索引（有疑问的读者可以回顾一下上述第一节中讲解B树的部分）。

同样道理，R树的非叶子结点存放的数据结构为：(I, child-pointer)。

其中，child-pointer是指向孩子结点的指针，I是覆盖所有孩子结点对应矩形的矩形。这边有点拗口，但我想不是很难懂？给张图：

D,E,F,G为孩子结点所对应的矩形。A为能够覆盖这些矩形的更大的矩形。这个A就是这个非叶子结点所对应的矩形。

这时候你应该悟到了吧？无论是叶子结点还是非叶子结点，它们都对应着一个矩形。树形结构上层的结点所对应的矩形能够完全覆盖它的孩子结点所对应的矩形。根结点也唯一对应一个矩形，而这个矩形是可以覆盖所有我们拥有的数据信息在空间中代表的点的。

我个人感觉这张图画的不那么精确，应该是矩形A要恰好覆盖D,E,F,G，而不应该再留出这么多没用的空间了

/

R树 详解

BB 树的搜索本质上是一维区间的划分过程，每次搜索节点所找到的子节点其实就是一个子区间。RR 树是把 BB 树的思想扩展到了多维空间，

采用了 BB 树分割空间的思想，是一棵用来存储高维数据的平衡树。

          

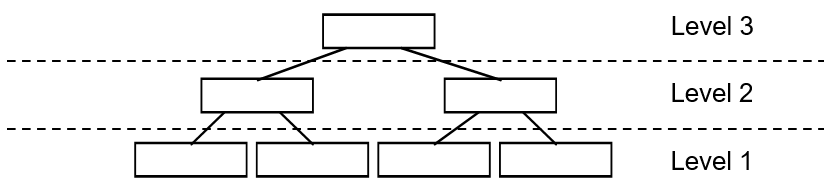
对于一棵 RR 树，叶子节点所在层次称为 Level1Level1，根节点所在层次称为 LevelhLevelh。一棵 RR 树满足如下性质：

    1）除根结点之外，所有非根结点包含有 mm 至 MM 个记录索引（条目）。根结点的记录个数可以少于 mm。通常 m=M2m=M2。

    2）每一个非叶子结点的分支数和该节点内的条目数相同，一个条目对应一个分支。所有叶子结点都位于同一层，因此 RR 树为平衡树。

    3）叶子结点的每一个条目表示一个点。

    4）非叶结点的每一个条目存放的数据结构为：(I,child−pointer)(I,child−pointer)。child−pointerchild−pointer 是指向该条目对应孩子结点的指针。II 表示

       一个 nn 维空间中的最小边界矩形(minimumboundingrectangleminimumboundingrectangle，即 MBRMBR)，II 覆盖了该条目对应子树中所有的矩形或点。

          

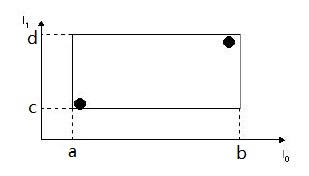
       两个黑点保存在一个叶子节点的两个条目中，恰好框住这两个条目的矩形表示为：I=(I0,I1)I=(I0,I1)。其中 I0=(a,b),I1=(c,d)I0=(a,b),I1=(c,d)，也就

       是说最小边界矩形是用各个维度的边来表示，在三维空间中那就是立方体，用 33 条边就可以表示了。

下面构建一棵 RR 树。如下左图，理论上，点可以任意组合成叶节点，只要 MBRMBR 包含它子树中的所有点。特别是 MBRMBR 可以重叠。下面

右图是另一种组合建立的 RR 树。

 

   

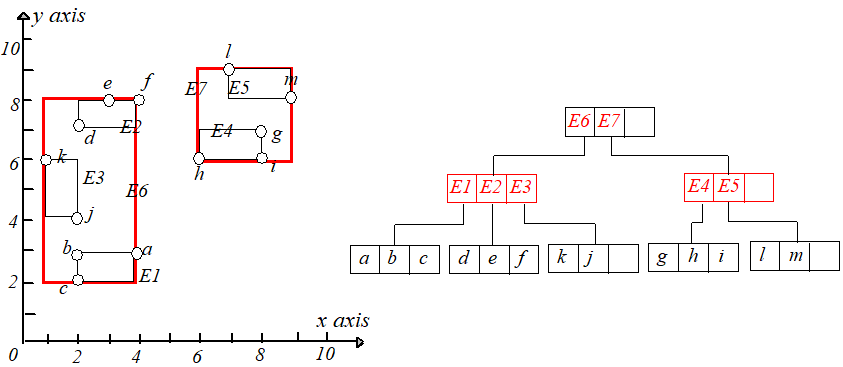
哪种分组更好呢？一般分组的原则就是最小化每个 MBRMBR 矩形，这样查询的时候发生的相交情况会越少，查询的分支就越少，查询效率越高。

R-tree 查询

介绍查询之前，需要先了解下：如何判断两个线段或者两个矩形是否相交？

    

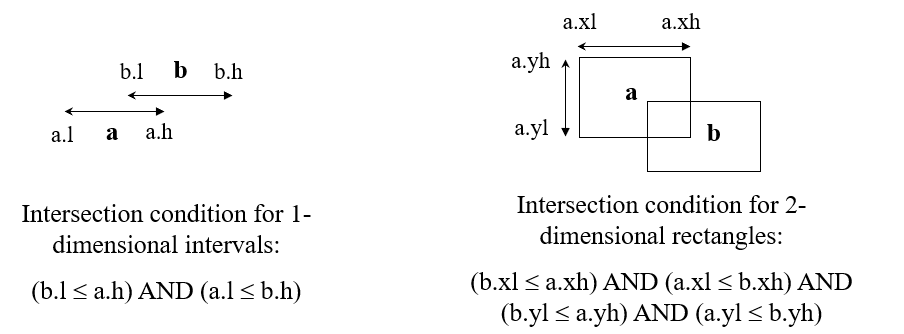
1. Range Query

   这种查询输入的是一个矩形所表示的范围，要求输出该范围内的所有点。从根节点开始，通过判断目标矩形和节点内的每一个条目对应的

   矩形是否相交来选择下一步查询的节点，如果有多个条目都相交，那对应的各个分支都得查。到达叶子节点后，就判断该叶子节点的每一

   个条目是否在查询区域内即可。

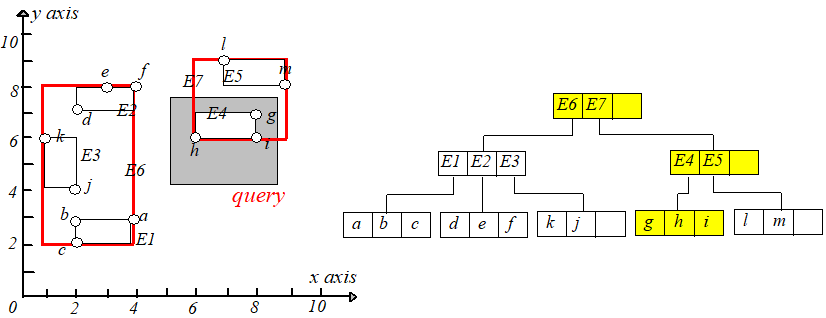
   现在想查询在矩形 [5,8.5],[4,7.5][5,8.5],[4,7.5] 内的所有点，即下图中的阴影矩形，设该矩形为 qq。首先判断 E6.I,E7.IE6.I,E7.I 和 qq 是否相交，发现 E7.IE7.I

   与 qq 相交，于是通过 E7E7 中的 child−pointerchild−pointer 指针到达孩子节点，再判断 E4.I,E5.IE4.I,E5.I 和 qq 是否相交，发现 E4.IE4.I 与 qq 相交，接下来

   就到达叶子节点了，然后判断每个点是否在矩形 qq 内即可，如果在则输出。

   

2. Nearest Neighbor Query 

   这种查询输入的是一个点，要求输出离这个点最近的 kk 个点，所以又叫 k−NNk−NN 查询。首先需要知道如何定义一个点到一个矩形的最

   短距离，记点 qq 到矩形 EE 的最短距离为 mindist(q,E)mindist(q,E)。规定：以 qq 为圆心，与 EE 有交点的最小圆的半径就是 mindist(q,E)mindist(q,E)。 

   k−NNk−NN 查询有两种算法，下面一一介绍。

   1）Depth-First NN Algorithm

      假设 k=1k=1，即查找距 qq 最近的一个点。

      输入一个点 qq，从根节点开始，计算 qq 到每个条目对应矩形的最短距离，即 mindist(q,E6.I),mindist(q,E7.I)mindist(q,E6.I),mindist(q,E7.I)，计算完后从小到大排序。

      因为 mindist(q,E6.I)<mindist(q,E7.I)mindist(q,E6.I)<mindist(q,E7.I)，所以来到 E6E6 的孩子节点，同样计算 mindist(q,E1.I),mindist(q,E2.I),mindist(q,E3.I)mindist(q,E1.I),mindist(q,E2.I),mindist(q,E3.I)，

      并从小到大排序，如下右图。

      

     

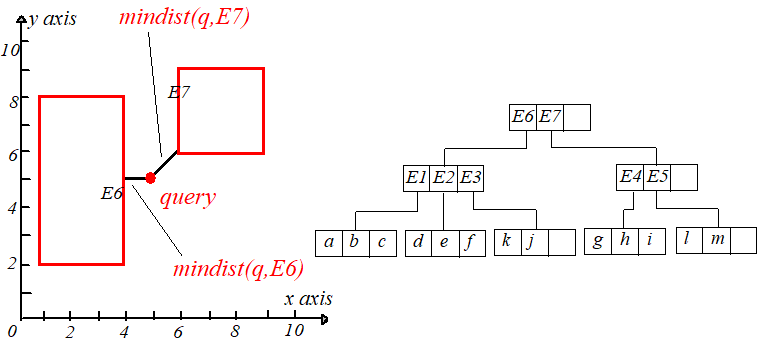
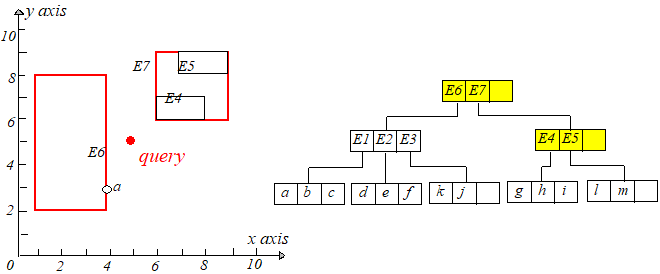
      qq 到 E1.IE1.I 和 E2.IE2.I 有相同的最短距离，于是随机选择一个，这里选择 E1E1，于是来到 E1E1 的叶子节点。计算点 a,b,ca,b,c 到 qq 点的距离，

      保存距离 qq 最近的那个点的距离，显然 a,qa,q 距离最近，这个距离记为 rr，这个 rr 只是当前搜索结果。接下进行回溯，回到上一个节点，注意

      qq 到所经过节点每个条目的最短距离都已经算好并升序排列，现在选择距离 qq 第二近的那个条目即 E2E2，此时有一步很重要的剪枝操作，需要

      判断mindist(q,E2.I)mindist(q,E2.I) 和 rr 的大小，如果 mindist(q,E2.I)>rmindist(q,E2.I)>r，那显然没有必要再去搜索它的子树了，因为E2E2 区域中的点到 qq 的距离不

      可能会比 rr 小了。

      接下来回溯到根节点，因为 mindist(q,E7.I)<rmindist(q,E7.I)<r，所以在 E7E7 区域中可能存在到 qq 的距离比 rr 小的点，需要搜索。来到 77 的孩子节点，

      计算 mindist(q,E4.I),mindist(q,E5.I)mindist(q,E4.I),mindist(q,E5.I) 并升序排列，接下来访问 E4E4 的孩子节点，发现 q,hq,h，的距离小于 rr，于是用新的最短距离更新 rr。

      

    

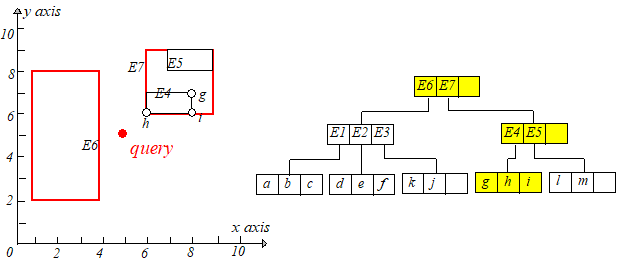
      然后再回溯，在已升序排列的数组里取下一个节点，判断是否剪枝。。。。

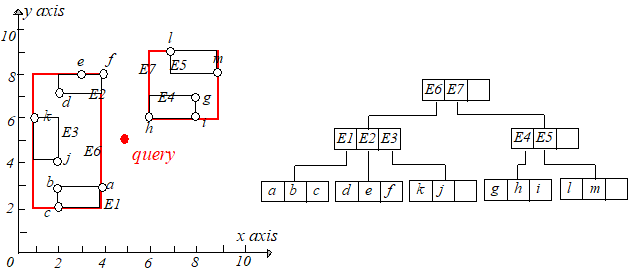
      当 k=2k=2 时，过程也是一样的，只不过要保存两个距离(最短和次短)，并使用次短距离进行剪枝。过程如下：

      a. Root => child node of E6 => child node of E1 => find {a, b} here

            b.   Backtrack to child node of E6 => child node of E2 (its mindist < dist(q, b)) => update the result to {a, f}

            c.   Backtrack to child node of E6 => child node of E3 => backtrack to the root => child node of E7 => child node of E4 => update the result to {a, h}

            d.   Backtrack to child node of E7 => prune E5 => backtrack to the root => end.

              

   2）Best-First Algorithm

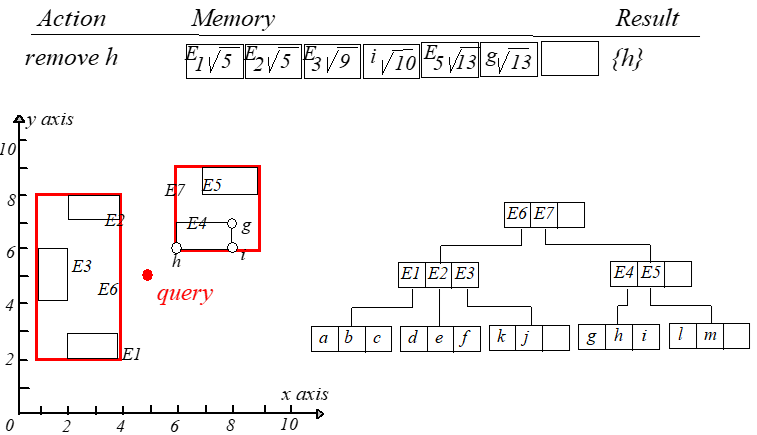
      这个算法需要维护一张点 qq 到所访问条目的最短距离表，这张表按升序排列，直接来看一下搜索过程。

      访问根节点的时候计算 mindist(q,E6.I),mindist(q,E7.I)mindist(q,E6.I),mindist(q,E7.I)，分别保存为位置 00 和 11。每一次迭代都访问第一个元素。计算 qq 

      到新结点每个条目的最短距离，然后更新表并重新排序。整个过程如下图所示，从左往右，从上到下阅读。

    

     

         

        

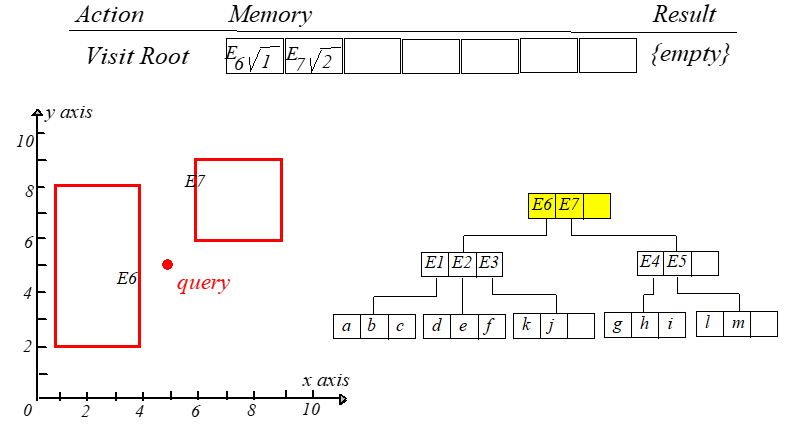
      此时就可以得到点 hh 到 qq 的距离最短。如果 k=2k=2，则继续搜索。   

       

      

R-tree 插入

插入的可以是一个点，也可以说是一个 RR 树。

1. 插入一个点 pp

   设根节点为 NN，遍历 NN 中所有条目，找出添加该点后 E.IE.I 扩张最小的条目(代价最小)，并把该条目对应的孩子节点定义为 FF。如果有多

   个这样的条目，那么选择面积最小的条目。将 NN 设为 FF，开始上述重复操作直到找到一个叶子节点。

   如果选择出来的叶子节点有足够的空间来放置点 pp，则直接添加一个条目就可以了。如果没有足够的空间，即插入后该叶子节点含有的条目高

   于 MM，则需要进行节点分裂。分裂方法如下：

   将插入 pp 后的叶子节点分裂为两个结点 LL 与 LLLL，这两个结点包含了原来叶子节点 LL 中的所有条目与新条目。

   将 NN 设为 LL，设 PP 为 NN 的父节点，ENEN 为父节点 PP 中指向 NN 的条目。调整 EN.IEN.I 以保证所有在 NN 中的条目都被恰好包围。

   创建一个指向 NNNN 的条目 ENNENN。如果 PP 有空间来存放 ENNENN，则将 ENNENN 添加到 PP 中。如果没有，则对 PP 进行分裂操作得到 PP

   和 PPPP。设 NN 为 PP，NNNN 为 PPPP，按相同的规则继续向上层传播。

   如果结点分裂，且该分裂向上传播导致了根结点的分裂，那么需要创建一个新的根结点，并且让它的两个孩子结点分别为原来那个根结点分裂

   后的两个结点，RR 树增高，程序结束。

   举个例子，假设 M=3M=3，把点 p(3,5)p(3,5) 插入到 RR 树中，根据最小调整代价原则，最终选择将点 pp 插入到 E3E3 中。如下图所示。

   

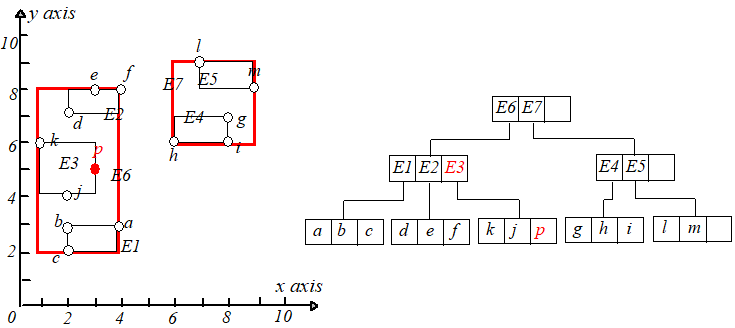
   接下来继续插入点 s(2,5)s(2,5)，点 ss 应该被插入到 E3E3 指向的叶子节点中，但是插入后该叶子节点的条目变成了 44(>M)，于是需要进行节点分裂。

   将 k,s,j,pk,s,j,p 分裂为两个叶子节点，分别包含 k,sk,s 和 j,pj,p，并调整 E3.IE3.I，然后为新节点(包含 j,pj,p)创建一个新条目 E8E8。

   

   

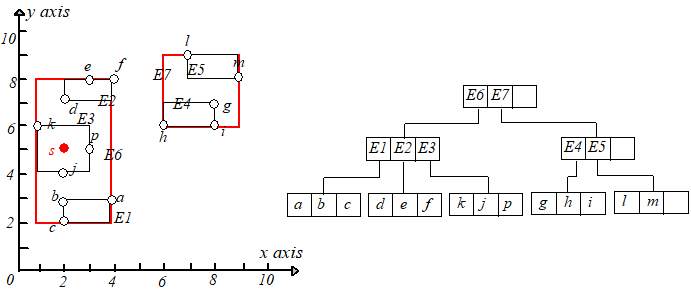
   但是 E8E8 和 E1,E2,E3E1,E2,E3 放在一起又会时节点条目数超过 MM，所以需要再进行节点分裂，根据最小 MBRMBR 原则，将 E2,E3E2,E3 放到一起，E1,E8E1,E8

   放到一起，调整 E6.IE6.I 的大小使其适配节点 E2,E3E2,E3，为节点 E1,E8E1,E8 创建一个新的条目 E9E9，插入到根节点，如下图所示：

   

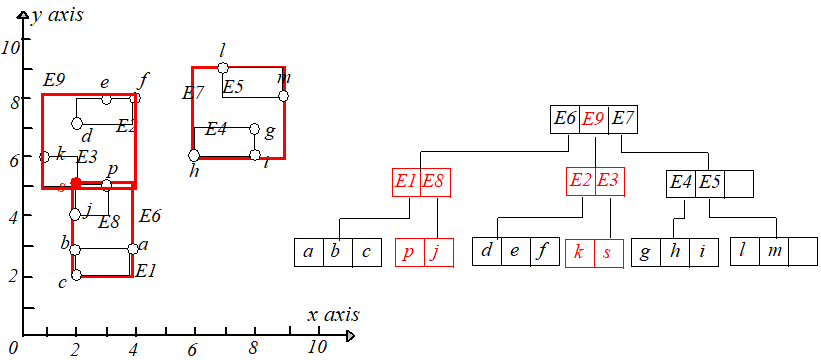
2. 插入一棵 RR 树

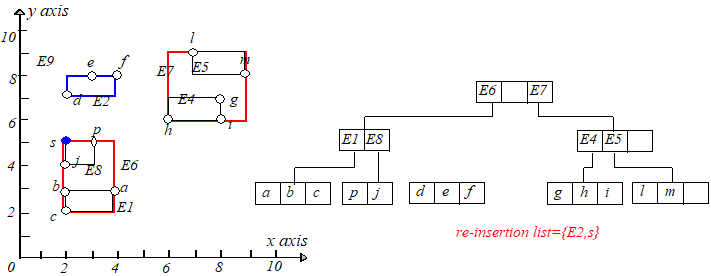
   插入一棵 RR 树其实插入的是 RR 树根节点所有条目所表示的矩形。和插入一个点一样，在选择条目的时候都是采用扩张最小代价原则。

   不同的是：插入一个点，最终是一定会插入到叶子节点中，但是插入 RR 树的时候，由于 RR 树本身有高度，假设它的高度为 HH，那么

   该它会被插入到 LevelHLevelH 层。

   举个例子，向树中插入 E2E2 这课 RR 树，因为它的高度为 22，所以 E2E2 会被插入到 Level2Level2。

   

   

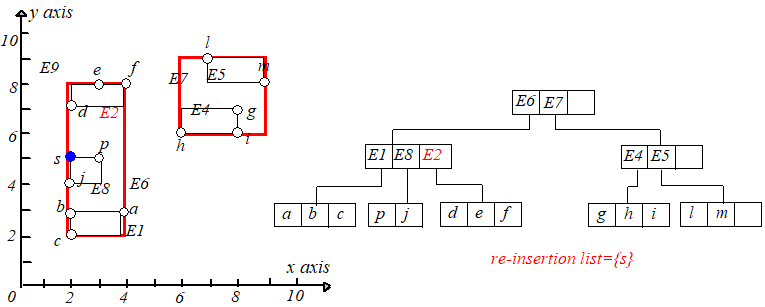
R-tree 删除

从 RR 树中删除一个点，首先需要找到该点所在的叶子节点，通过判断点是否在条目所对应的矩形区域内来选择分支，直到找到叶子

节点，判断所要删除的点是否在该叶子节点内，如果在则删除，并调整父节点对应题目的矩形。删除之后，如果叶子节点剩余条目数过

少，即小于要求的最小值 mm，则需要进行调整，令 NN 为条目数低于下限的叶子节点，调整步骤如下。

初始化一个用于存储被删除结点包含的条目的链表 QQ。令 PP 为 NN 的父结点，ENEN 为 PP 结点中存储的指向 NN 的条目。

因为 NN 含有条目数少于 mm，于是从 PP 中删除 ENEN，并把结点 NN 中的条目添加入链表 QQ 中，然后输出节点 NN。

往上层走，令 NN 等于 PP，继续进行下溢判断，如果下溢，则将该节点中的每个条目加到 QQ 中，删除该结点和父节点中对应条目。

如果没有下溢，不要忘记调整祖父节点对应条目的矩形形状。

所有在 QQ 中的结点中的条目需要被重新插入。原来属于叶子结点的条目可以使用 Insert 操作进行重新插入，而那些属于非叶子结点

的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层(相当于插入一棵 RR 树)。

举个例子，删除点 k(1,6)k(1,6)，从根节点开始找，可以找到 E3E3，将其删除，但是下溢了。具体过程如下图：

   

    

   

    

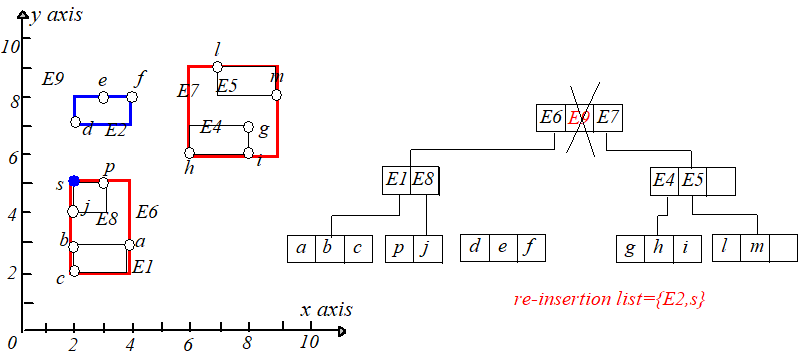
接下来将 QQ 中的项重新插入到 RR 树中。

   

    

///

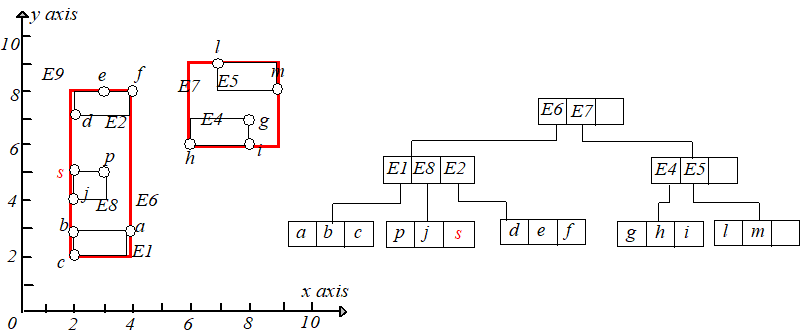
高级数据结构之 R 树

R树（R-tree）是一种将Ｂ树扩展到多维情况下得到的数据结构，它最初由Antonin Guttman于1984年提出。Ｂ树的结点中会存储一个键的集合，这些键把线分成片段，沿着那条线的点仅属于一个片段。因此，Ｂ树使得我们可以很容易地找到点。如果把沿线各处的点表示成Ｂ树结点，我们就能够确定点所属唯一子结点，在那里可以找到该点。

Antonin Guttman在他提出Ｒ树的经典论文中给出的Ｒ树例子

Ｒ树表示由二维或者更高维区域组成的数据，我们把它们称为数据区。一个Ｒ树的内结点对应于某个内部区域，或称“区域”，它不是普通的数据区。原则上，区域可以是任意形状，虽然实际中它经常为矩形或其他简单形状。例如上图中（a）是一棵Ｒ树，其中的一个内部结点R3R4R5就代表（b）中的一个区域，它被包含在R1之中。Ｒ树的结点用子区域替代键，子区域表示结点的子结点的内容，例如R3、R4、R5是结点R3R4R5中的键，它们中的每一个都表示（b）中的一个子区域。注意，子区域没有覆盖整个区域，只要把位于大区域内的所有数据区都完全包含在某个小区域中就合乎要求。进一步说，子区域允许有部分重叠，例如R3和R4就彼此互有重叠。当然，我们希望重叠的部分尽可能地小。

一、Ｒ树（R-tree）的定义

在R-tree中首先要明确的一个概念是Bounding Box （或者简写为BB）。前面已经讲过，区域可以是任意形状，但实际中它经常为矩形，此时我们就将包含有一组对象的一个矩形称为BB。例如上图中的R3就是一个BB，其中包含的对象有R8、R9、R10。再比如，下图中的左图里给出了一组对象，右图中的绿色区域就是一个BB。

 在BB的概念之上，还可以定义最小BB（Minimum Bounding Box），也就是包含一组对象的最小矩形。例如下图中所给出的绿色区域就是一个最小BB。

 通常可以用一个矩形区域的左下角和右上角的坐标来表示该矩形，例如下面这个矩形就可以表示成（(10, 20), (50, 40)）。

 基于上述概念，现在我们终于可以正式地考察R-tree了。R-tree是一种将Ｂ树扩展到多维情况下得到的索引树结构。它的内部结点包含了若干条目（entries），这些条目中的每一个都具有如下格式（BB, 指向孩子结点的指针），例如：

 R-tree的叶子结点同样也包含有若干条目，这些条目中的每一个都具有如下格式（最小BB, 指向对象的指针），也就是说叶子结点中包含了指向记录（record）的索引。例如：

 如下图所示，作为一种索引树结构，R-tree的重要性质就是对于一个给定的内部结点（, ptr）而言，指向孩子结点的指针ptr指向了一些对象，而这些对象必然完全包含在中。

 来看一个具体的例子，假设有下面左图所示的一些对象：road1, road2, house1, house2, school, pop, pipeline。现在需要构建一棵R-tree来将这些对象表示出来。首先，如右图所示，road1, road2, house1是完全包含在((0, 0), (60, 50))这个BB中的。

 另外，如左图所示，school, pop, house2 和pipeline是完全包含在((20, 20), (100, 80))这个BB中的。如果采用上述这几个BB，那么构建出来的R-tree就如下面的右图所示。

 一个重要的注意事项是：Ｒ树的结点里使用的BB是可以彼此重叠的（overlap），这一点在本文最开始给出的图示中即有明确的表达，而上面这个刚刚建立的Ｒ树的两个内部结点之间也有重叠的部分。

二、在Ｒ树中进行搜索

这里需要提醒读者的一点是，Ｒ树是可以扩展多更高维度情况的，不失普遍性地，这里我们仅以最简单的情况，也就是针对二维的情况来进行讨论。现实中，这也是应用最为广泛的场景。例如，在地图（或者地理信息系统）上进行位置的存储与查询都属于是二维的情况。此时，在Ｒ树中进行搜索操作的目的可以是找到一个具体的位置（即一个点）Point(x,y)，如果某个叶子所表示的区域中包含了该点，则返回这个叶子，否则就返回空（也就是找不到）。Ｒ树的搜索算法是从根开始递归进行的。假设当前结点为n，下面伪代码给出了从此出发递归搜索Point(x,y)的过程。

Lookup( (x, y), n, result )
{
　　　　// n = current node of the search in the R-tree
　　　　if ( n == internal node )
　　　　{
　　　　　　　　for ( each entry ( BB,  childptr ) in node n ) do         
　　　　　　　　{
　　　　　　　　　　　　/* ====================================
	         　　　　　　Look in subtree if (x,y) is in box
		 　　　　==================================== */
　　　　　　　　　　　　if ( (x,y) ∈ BB )
　　　　　　　　　　　　{
　　　　　　　　　　　　　　　　Lookup( (x,y),  childptr, result);
　　　　　　　　　　　　}
　　　　　　　　}
　　　　}
　　　　else
　　　　{
　　　　　　　　for ( each object Ob in node n ) do
　　　　　　　　{
　　　　　　　　　　　　if ( (x,y) ∈ MBB(Ob) )
　　　　　　　　　　　　{
　　　　　　　　　　　　　　　　Add Ob to result;
　　　　　　　　　　　　}
　　　　　　　　}
　　　　}
｝

可见，在Lookup函数中：

• 如果n是一个内部结点，那么就逐个搜索其中的条目，如果Point(x,y)被包含在某个条目所给定的BB中，就递归搜索它的孩子。
• 如果n是一个叶子结点，那么就逐个搜索其中的对象，如果Point(x,y)被包含在某个对象的最小BB（MBB）中，则返回该对象作为结果。

下面来看一个具体的例子，现在的任务是要在前面已经建立好的Ｒ树中搜索点P(40,75)。

 从根结点开始，因为它不是叶子结点，所以逐个搜索其中的条目，点P(40,75)并不位于((0,0), (60,50))这个BB中，但它位于((20,20), (100,80))这个BB中，所以递归地搜索该子树。如下图所示：

 此时，我们已经达到了一个叶子结点，因此逐个搜索其中的对象，发现P(40,75)位于对象school的MBB中，因此最后应该返回该对象作为结果。

 此外，在Ｒ树中进行搜索操作的目的也可以是找到一个对象。这里，我们将问题简化，即用包含该对象的MBB来表示该对象。例如，在下图中，我们要搜索的是一个圆形区域，那么就可以用它的MBB，即((20,50), (45,60))，来表示该对象。

 下面来谈一下BB的“包含关系”。假设Ａ是一个BB，它被包含在另外一个记为Ｂ的BB中，其充要条件为：

• x_LL(B)≤x_LL(A)  并且　y_LL(B)≤y_LL(A)
• x_UR(A)≤x_UR(B)  并且　y_UR(A)≤y_UR(B)

其中，角标LL表示左下，UR表示右上。下面的图示解释了这种关系，这里不再赘述。

 定义了包含关系之后，我们就可以利用Ｒ树来进行object搜索了。这里的object是指一小块区域，或者在某个特定位置上的任意形状。这与前面介绍的“在Ｒ树中进行点搜索”的算法是一样的。也就是说某个BB包含该object，就递归搜索它的孩子。如果某个最小BB包含该object，则返回表示该BB的对象。

Ｒ树在对维数据管理中具有重要应用。在Ｒ树被提出之后，又有许多改进型的数据结构被发展处理，例如比较有代表性的Hilbert R树。笔者将会在后续的文章中更加深入地介绍向Ｒ树中插入新对象的方法，即Ｒ树的插入算法。

参考文献与推荐阅读材料

【１】Hector G. Molina, Jeffrey D. Ullman, Jennifer Widom，数据库系统全书，机械工业出版社

【２】Guttman, Antonin. R-trees: a dynamic index structure for spatial searching. Vol. 14. No. 2. ACM, 1984.

【３】美国埃默里大学Shun Yan Cheung副教授Advanced Database Systems的授课材料（链接）

///