定义
T
=
{
t
k
}
k
=
1
K
T=\{t_k\}^K_{k=1}
T={tk}k=1K:静止姿态下的关节点坐标。
R
=
{
R
p
a
(
k
)
,
k
}
k
=
1
K
R=\{R_{pa(k), k}\}_{k=1}^K
R={Rpa(k),k}k=1K:相对旋转。
Q
=
{
q
k
}
k
=
1
K
Q=\{q_k\}^K_{k=1}
Q={qk}k=1K:根据输入的相对旋转,FK计算出的关节点坐标。
K
K
K: 关节点数目。
p
a
(
k
)
pa(k)
pa(k):第k个节点的父节点。
R
p
a
(
k
)
,
k
R_{pa(k), k}
Rpa(k),k:第k个节点关于其父节点的相对旋转。
前向动力学:
q k = R k ( t k − t p a ( k ) ) + q p a ( k ) (1) q_k = R_k(t_k - t_{pa(k)}) + q_{pa(k)} \tag{1} qk=Rk(tk−tpa(k))+qpa(k)(1)
R k = R p a ( k ) R p a ( k ) , k (2) R_k=R_{pa(k)}R_{pa(k),k} \tag{2} Rk=Rpa(k)Rpa(k),k(2)
R k ∈ S O ( 3 ) R_k\in SO(3) Rk∈SO(3):第k个节点关于标注静止姿态空间的全局旋转。
反向动力学:
IK是FK的逆过程,输入静止姿态
T
T
T和目标姿态
P
P
P, 计算相对旋转矩阵
R
R
R
R
=
I
K
(
P
,
T
)
(3)
R = IK(P, T) \tag{3}
R=IK(P,T)(3)
理想情况下,求得的旋转矩阵需要满足如下条件:
p
k
−
p
p
a
(
k
)
=
R
k
(
t
k
−
t
p
a
(
k
)
)
∀
1
≤
k
≤
K
(4)
p_k - p_{pa(k)} = R_k(t_k - t_{pa(k)}) \quad \forall 1 \leq k \leq K \tag{4}
pk−ppa(k)=Rk(tk−tpa(k))∀1≤k≤K(4)
FK问题是适定的,IK问题却是病态的,要么无解,要么可能存在许多解可以目前上述条件。
运动学树
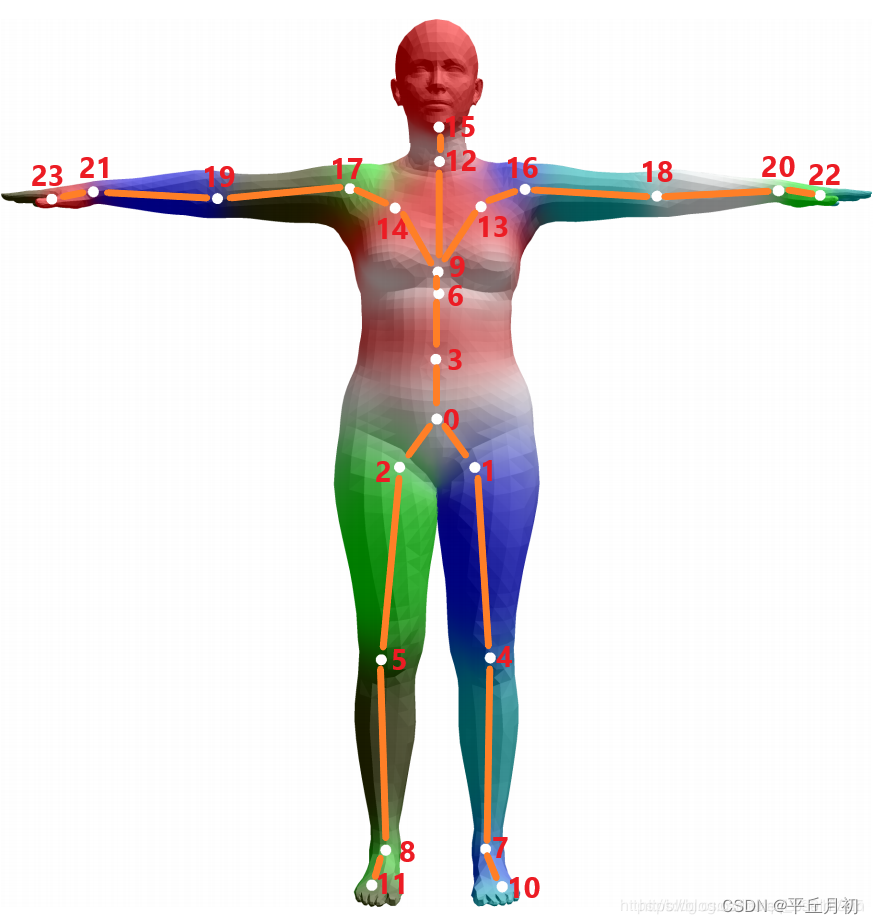
Naive HybrIK
类似FK过程,IK过程可以沿着运动学树迭代进行。
首先,我们要确定根节点的全局旋转
R
0
R_0
R0,可以通过spine, left hip, right hip这三个点的位置和SVD分解求得闭式解。
之后的每一步,以第k步为例,我们假设其父节点
R
p
a
(
k
)
R_{pa(k)}
Rpa(k)的旋转已知, 根据公式(1)和(2)可得:
R
p
a
(
k
)
−
1
(
p
k
−
p
p
a
(
k
)
)
=
R
p
a
(
k
)
,
k
(
t
k
−
t
p
a
(
k
)
)
(5)
R^{-1}_{pa(k)}(p_k - p_{pa(k)}) = R_{pa(k),k}(t_k - t_{pa(k)}) \tag{5}
Rpa(k)−1(pk−ppa(k))=Rpa(k),k(tk−tpa(k))(5)
p k ⃗ = R p a ( k ) − 1 ( p k − p p a ( k ) ) t k ⃗ = t k − t p a ( k ) \begin{aligned} \vec{p_k} &= R^{-1}_{pa(k)}(p_k - p_{pa(k)}) \\ \vec{t_k} &= t_k - t_{pa(k)} \end{aligned} pktk=Rpa(k)−1(pk−ppa(k))=tk−tpa(k)
可以通过下式计算相对旋转:
R
p
a
(
k
)
,
k
=
D
(
p
k
⃗
,
t
k
⃗
,
ϕ
k
)
R_{pa(k), k} = D(\vec{p_k}, \vec{t_k}, \phi_k)
Rpa(k),k=D(pk,tk,ϕk)
ϕ
k
\phi_k
ϕk是网络预测出的第k个节点的twist角。twist角的集合表示为
Φ
=
{
ϕ
k
}
k
=
1
K
\Phi=\{\phi_k\}_{k=1}^K
Φ={ϕk}k=1K,因为旋转矩阵是正交阵,因此
R
p
a
(
k
)
−
1
=
R
p
a
(
k
)
T
R^{-1}_{pa(k)}=R^{T}_{pa(k)}
Rpa(k)−1=Rpa(k)T,使得解算过程可微。
完整的算法流程如下:
输入:Q, T,
Φ
\Phi
Φ
输出:R
第一步先确定根节点0的全局旋转,再沿着运动学树进行下述迭代处理
p
k
⃗
←
R
p
a
(
k
)
−
1
(
p
k
−
p
p
a
(
k
)
)
t
k
⃗
←
t
k
−
t
p
a
(
k
)
R
p
a
(
k
)
,
k
s
w
←
D
s
w
(
p
k
⃗
,
t
k
⃗
)
R
p
a
(
k
)
,
k
t
w
←
D
t
w
(
p
k
⃗
,
ϕ
k
⃗
)
R
p
a
(
k
)
,
k
←
R
p
a
(
k
)
,
k
s
w
R
p
a
(
k
)
,
k
t
w
\begin{aligned} \vec{p_k} &\leftarrow R^{-1}_{pa(k)}(p_k - p_{pa(k)}) \\ \vec{t_k} & \leftarrow t_k - t_{pa(k)} \\ R^{sw}_{pa(k), k} & \leftarrow D^{sw}(\vec{p_k}, \vec{t_k} ) \\ R^{tw}_{pa(k), k} & \leftarrow D^{tw}(\vec{p_k}, \vec{\phi_k} ) \\ R_{pa(k),k} & \leftarrow R^{sw}_{pa(k), k}R^{tw}_{pa(k), k} \end{aligned}
pktkRpa(k),kswRpa(k),ktwRpa(k),k←Rpa(k)−1(pk−ppa(k))←tk−tpa(k)←Dsw(pk,tk)←Dtw(pk,ϕk)←Rpa(k),kswRpa(k),ktw
R s w = D s w ( p ⃗ , t ⃗ ) = I + s i n α [ n ⃗ ] × + ( 1 − c o s α ) [ n ⃗ ] × 2 R^{sw} = D^{sw}(\vec{p}, \vec{t}) = I + sin\alpha[\vec{n}]_{\times} + (1 - cos\alpha)[\vec{n}]_{\times}^2 Rsw=Dsw(p,t)=I+sinα[n]×+(1−cosα)[n]×2
R
t
w
=
D
t
w
(
p
⃗
,
ϕ
)
=
I
+
s
i
n
ϕ
∣
∣
t
⃗
∣
∣
[
n
⃗
]
×
+
(
1
−
c
o
s
ϕ
)
∣
∣
t
⃗
∣
∣
2
[
n
⃗
]
×
2
R^{tw} = D^{tw}(\vec{p}, \phi) = I + \frac{sin\phi}{||\vec{t}||}[\vec{n}]_{\times} + \frac{(1 - cos\phi)}{||\vec{t}||^2}[\vec{n}]_{\times}^2
Rtw=Dtw(p,ϕ)=I+∣∣t∣∣sinϕ[n]×+∣∣t∣∣2(1−cosϕ)[n]×2
n
⃗
=
t
⃗
×
p
⃗
∣
∣
t
⃗
×
p
⃗
∣
∣
\vec{n} = \frac{\vec{t}\times\vec{p}} {||\vec{t} \times \vec{p}||}
n=∣∣t×p∣∣t×p
[
t
⃗
]
×
[\vec{t}]_{\times}
[t]×是
t
⃗
\vec{t}
t的对称矩阵。
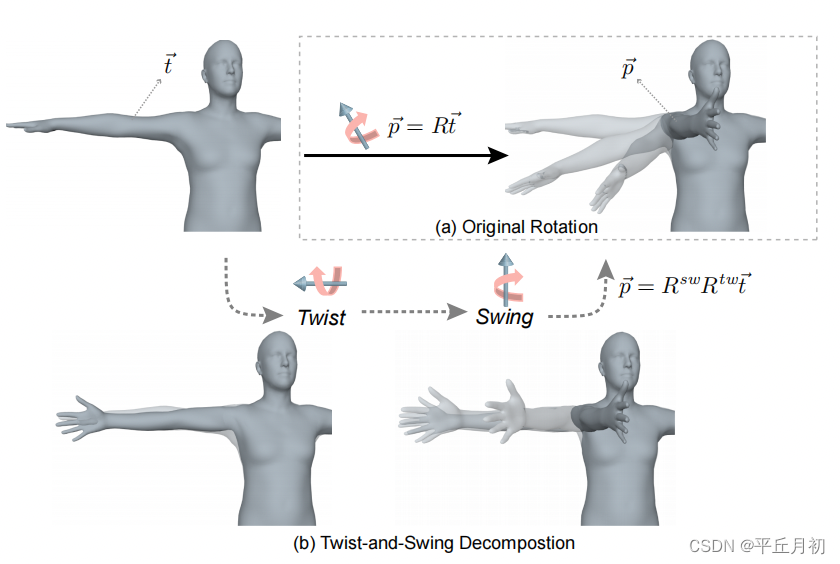
Adaptive HybrIK
Naive HybrIK过程看着是有效的,它遵循了
∣
∣
q
k
−
q
p
a
(
k
)
∣
∣
=
∣
∣
t
k
−
t
p
a
(
k
)
∣
∣
||q_k - q_{pa(k)}||=||t_k - t_{pa(k)}||
∣∣qk−qpa(k)∣∣=∣∣tk−tpa(k)∣∣这个假设。
但不幸的是,3D关键点估计方法的预测结果,并不总是能和静止姿态模板一致。如果使用Naive HybrIK的方式,这个误差会沿着运动学树一直累计。
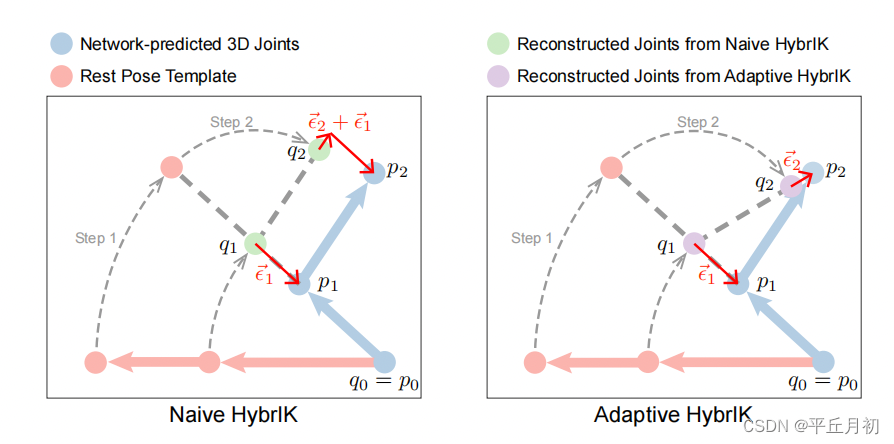
q p a ( k ) ← R p a ( k ) ( t p a ( k ) − t p a 2 ( k ) ) + q p a 2 ( k ) p k ⃗ ← R p a ( k ) − 1 ( p k − q p a ( k ) ) t k ⃗ ← t k − t p a ( k ) R p a ( k ) , k s w ← D s w ( p k ⃗ , t k ⃗ ) R p a ( k ) , k t w ← D t w ( p k ⃗ , ϕ k ⃗ ) R p a ( k ) , k ← R p a ( k ) , k s w R p a ( k ) , k t w \begin{aligned} q_{pa(k)} &\leftarrow R_{pa(k)}(t_{pa(k)} - t_{pa^2(k)}) + q_{pa^2(k)} \\ \vec{p_k} &\leftarrow R^{-1}_{pa(k)}(p_k - q_{pa(k)}) \\ \vec{t_k} & \leftarrow t_k - t_{pa(k)} \\ R^{sw}_{pa(k), k} & \leftarrow D^{sw}(\vec{p_k}, \vec{t_k} ) \\ R^{tw}_{pa(k), k} & \leftarrow D^{tw}(\vec{p_k}, \vec{\phi_k} ) \\ R_{pa(k),k} & \leftarrow R^{sw}_{pa(k), k}R^{tw}_{pa(k), k} \end{aligned} qpa(k)pktkRpa(k),kswRpa(k),ktwRpa(k),k←Rpa(k)(tpa(k)−tpa2(k))+qpa2(k)←Rpa(k)−1(pk−qpa(k))←tk−tpa(k)←Dsw(pk,tk)←Dtw(pk,ϕk)←Rpa(k),kswRpa(k),ktw






















 17
17











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








