Weights Update

最新推荐文章于 2022-11-22 11:00:07 发布

铭霏

最新推荐文章于 2022-11-22 11:00:07 发布

阅读量1k

点赞数

分类专栏： Deeplearning

Deeplearning 专栏收录该内容

7 篇文章 1 订阅

订阅专栏

Weights Update 与 Dropout

Weights Update
- 参数更新Weights Update

参数更新：Weights Update

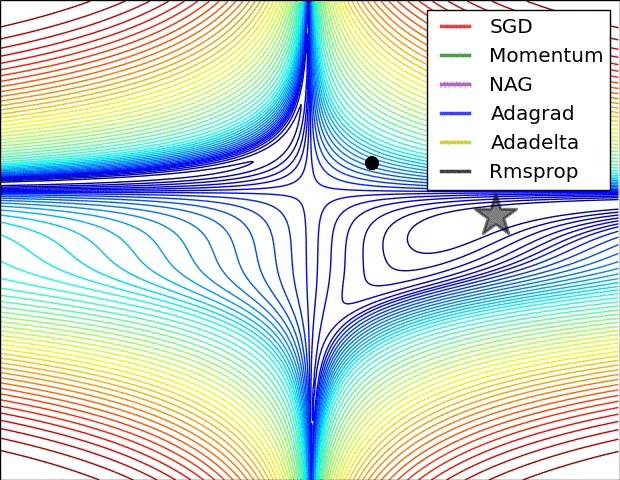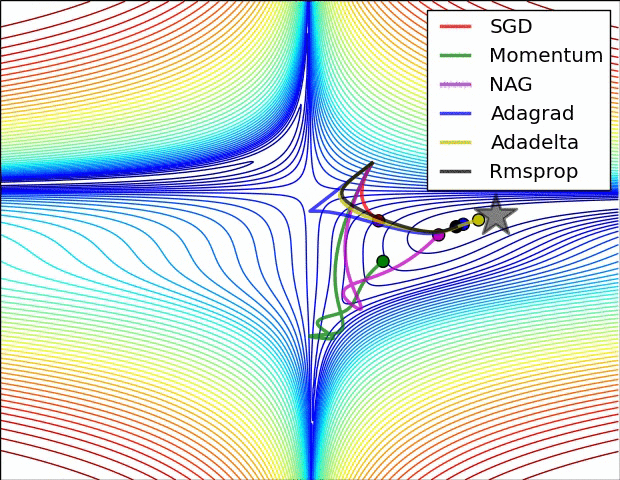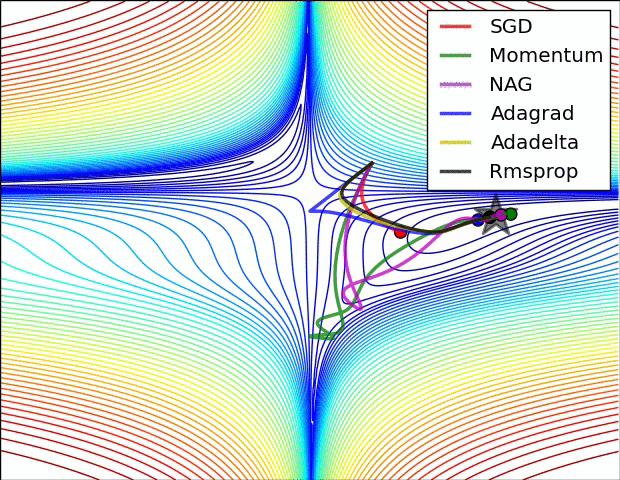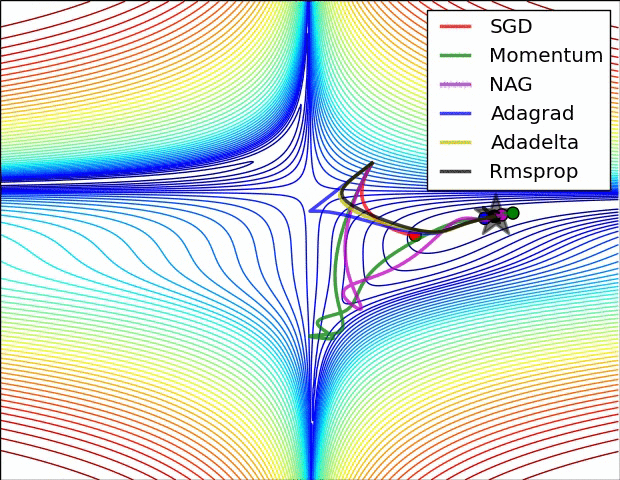
在进一步学习之前，先看看我们将要覆盖的权重更新方法的效果,图片来源：http://cs231n.github.io/neural-networks-3/

学习率是怎么来的

相信有机器学习基础的读者都很熟悉一个式子： W−=λdW ，这里的 λ 就是学习率，那么这个式子是怎么来的呢？（小编不敢在众大神面前班门弄斧，只是跟大家分享下，如果有什么改进，还望提出哦，谢谢！）
在传统的机器学习方法中，我们所遇到的一般都是凸问题（可以想象这种问题的Loss Function就想一个大锅，存在最小值），因此如果我们想要达到最小的Loss，我们就需要沿着这个函数的梯度方向往下走（即梯度下降），那么梯度方向就是 dW|dW| ，走的步长就是常数 Δ ，这时就会发现，如果用 W−=ΔdW|dW| 在梯度较大的时候，也就是比较最优解的时候，W的更新有点太不紧不慢了，然而到了梯度较小的时候，也就是较靠近最优解的时候，W的更新竟然也保持着跟原来一样的速率，这样会导致W很容易更新过度反而远离了最优解。所以这时候就想了，既然在远离最优解的时候梯度大，在靠近最优解的时候梯度小，为何不干脆把这个性质利用起来呢？于是我我们就用 λ|W| 来代替 Δ ，最后得到了我们熟悉的式子 W=W−λ|W|dW|dW|=W−λdW 。所以说这时的 λ 其实是具备了一些动态更新的特点的，别看它是个常数，但是显然，我们这里不是跟大家说这样就足够了，我们还可以权重得更好。也就是我下面要跟大家一起分享的其他几个Weights Update的方法。

随机梯度下降-Stochastic Gradient Descent

这种方法简称SGD（打这个名字好累，下面都用简称了= =）。SGD其实很简单，就是相比我们之前见到的Batch Gradient Descent方法使用全部数据做一轮迭代，SGD一轮迭代只用一条随机的数据，因此SGD的迭代次数会比BGD大很多，然而总体还是比BGD快。下面简单分析下SGD的优缺点。
优点:

收敛速度快(通过减少总体的迭代次数)
可以很快的见到效果

缺点：

收敛时浮动，不稳定
在最优解附近跳动，难以判断是否已经收敛
随机访问可能造成巨大的IO开销

Batch与SGD的合体?Mini-Batch Gradient Descent！

看到SGD的优缺点，我们不禁想，有没什么办法可以即保留绝大部分的优点，同时有大幅的减弱缺点呢？答案是肯定的！就是我们这里介绍的Mini-Batch Gradient Descent。道理也很简单，就是SGD太极端了，一次一条，为何不一次五十条呢？是的，这个方法就是用一次迭代多条数据的方法。并且如果Batch Size选择合理，不仅收敛速度比SGD更快，更稳定，而且在最优解附近的跳动也不会很大，甚至能够得到比Batch Gradient Descent 更好的解。这样就综合了SGD和Batch Gradient Descent 的优点，同时弱化了缺点。总之不用多想，Mini-Batch比SGD和Batch Gradient Descent都好。

再给力点？Momentum来了

上面两种都是随机的方法，因此都存在不同程度的震荡，因此，如果能够以之前下降的方向作为参考，那么将会有利于下一次下降的方向（这个是成立的，因为下降的方向的期望是指向最优解）。下面给出Momentum Update的Python代码：

v = momentum*v-learning_rate*dW
W += v
 
 1
2
 
 1
2

这里的v通常被称为第一moment。v可以初始化为0，momentum一般取0.5或0.9或0.99。从代码可以看出，在训练过程中，v不断积累和更新下降的速率和方向。从本节开头的动图也可以看出，Momentum的确比SGD快多了，但是由于有历史的影响，Momentum会出现越过最优解的情况，但是总体还是比单纯的随机方法快很多。

考虑得再多一些-Nesterov Momentum Update

NAG（Nesterov Accelerated Gradient）不仅仅把SGD梯度下降以前的方向考虑，还将Momentum梯度变化的幅度也考虑了进来。下面给出python的代码

v_prev = v
v = momentum*v-learning_rate*dx
x+=v+momentum*(v-v_prev)
 
 1
2
3
 
 1
2
3

从代码也可以看出，NAG多观察了Momentum拐弯的角度，因此，当Momentum在越过最优解的时候，Momentum会尽可能的希望拐回正轨，这时候NAG就会留意到Momentum在拐弯从而加速自己走回正轨的，所以我们看到动图中，NAG偏离最优解的程度更小些。

平衡梯度的更新策略-AdaGrad

在传统机器学习中，一种加速迭代速度的方法就是将数值归一化到一个一原点为中心的空间内，因为这样可以避免梯度在某些维度上跨度很小而拖慢迭代速度。而对于随机的方法，这种数值不同维度上的域的范围如果有很大的区别可能会导致非常糟糕的情况。试想一个二维的W，如果Loss Function对第二维的变化非常敏感，那么当随机方法在执行时，很有可能会在第二维处迈出了相对来说很大的一步，而在第一微处迈出了很小的一步，那么收敛效果就会不好。AdaGrad就是考虑到这种情况。AdaGrad通过不断积累每次随机梯度不同维度的大小，使得之后的梯度在该小的维度上小，该大的维度上大。下面给出AdaGrad的python代码

cache += dx**2
x+=-learning_rate*dx/(np.sqrt(cache)+1e-7)
 
 1
2
 
 1
2

这里的cache也常被称为第二moment。

尽量保持梯度的RMSProp方法

细心的读者可能会留意到，AdaGrad每次迭代都累加了梯度，这会导致在迭代后期，AdaGrad的梯度会变得很小，从而减慢了速度，RMSProp是Hinton在Coursera公开课上提出的方法，它尽可能的保持学习率不会下降得太快，下面给出python代码

cache = decay_rate*cache+(1-decay_rate)*dx**2
x+=-learning_rate*dx/(np.sqrt(cache)+1e-7)
 
 1
2
 
 1
2

这里的decay_rate一般取0.9或0.99

AdaDelta

相信大家一定也很好奇动图中那个飞得最好的AdaDelta是什么方法吧，然而课上并没有提到，于是小编就去谷歌了下，下面给出参考链接：

可能要教育网或者有数据库账号才能看吧….
http://arxiv.org/pdf/1212.5701.pdf

下面给出Python代码

cache_dx = delta*cache_dx + (1-delta)*(dx**2)
v = -learning_rate*np.sqrt(cache_x)*dx/(np.sqrt(cache_dx)+1e-7)
x += v
cache_x = delta*cache_x + (1-delta)*(v**2)

 
 1
2
3
4
5
 
 1
2
3
4
5

结合Momentum与AdaGrad：Adam Update

Momentum方法和AdaGrad方法都在解决权重更新不同的问题上有很大的作用，那么现在就将这两者合并起来，形成一个更加强大的方法，Adam。由于是两者的结合，那么我就不加赘述了，直接上代码

m = beta1*m+(1-beta1)*dx # update first moment
v = beta2*v+(1-beta2)*(dx**2) # update second moment
mb = m/(1-beta1**t) # correct bias
vb = v/(1-beta2**t) # correct bias
x+= -learning_rate*mb/(np.sqrt(vb)+1e-7) # RMSProp-like
 
 1
2
3
4
5
 
 1
2
3
4
5

提出者Kingma et al. 建议beta1初始值为0.9，beta2初始值为0.999。留意到上面代码多了一些我们没遇到过的，就是correct bias部分，这部分代码我们可以看到它除了(1-(小于1)**t)，可以知道，当t很大时，近似于除以1，因此这个代码只在前期的时候有作用，一个解释就是因为m和b初始值是置0的，加入这段代码是为了修正前期m和b。

逃不了的学习率

虽然方法越来越好，但是我们始终可以看到，learning_rate一直形影不离地跟着我们，因此，这些方法是否管用，首先是learning rate一定要合适。相信各位读者有一定的机器学习的方法的积累，这时我们自然而然地就能想到validation（或cross-validation）用来选择学习率，通常初始学习率设为0.01都会有个比较好的表现。我们希望在初期学习率大一些，权重更新的程度大些，而到了收敛阶段学习率小些，权重更新得谨慎一些。因此一般让学习率虽然迭代次数的增加而逐渐变小。
一般有这三种策略：