本次课程大纲:
1、 最优间隔分类器
2、 原始优化问题&对偶优化问题(KKT条件)
3、 SVM对偶问题
4、 核方法(下一讲)
复习:
支撑向量机中改动的符号:
输出y∈{-1,+1}
h输出的假设值也改为{-1,+1}
g(z) = { 1 , 如果z>=0; -1, 如果z<0}
hw.b(x)=g(wTx+b),这里的b相当于原来的θ0,w相当于原来θ除去θ0剩余部分,长度为n维。将截距b单提出来,方便引出支撑向量机。
函数间隔:
一个超平面(w,b)和某个特定训练样本(x(i),y(i))对应的函数间隔定义为:
参数(w,b)定义了一个分类器,例如定义了一个线性分界线。
如果y(i)=1,为了获得较大的函数间隔,需要令wTx(i)+b >> 0;
如果y(i)=-1,为了获得较大的函数间隔,需要令wTx(i)+b << 0
如果y(i)(wTx(i)+b) > 0,意味着分类结果正确
一个超平面(w,b)和整个训练集的函数间隔定义为:
即相对于整个训练集的函数间隔定义为所有相对于样本的函数间隔的最坏情形(上述讲到,分界线距离样本越远效果越好)。
几何间隔:
几何间隔定义为:
这个定义和函数间隔很相似,不同点是对向量w进行了标准化。同样,希望几何间隔也是越大越好。
结论:如果||w||=1,函数间隔等于几何间隔。更一般的,几何间隔等于函数间隔除以||w||。
一个超平面(w,b)和整个训练集的几何间隔定义为:
和函数间隔类似,取样本中最小的几何间隔。
性质:可以任意比例缩放w和b,因为任意缩放w和b都不会改变超平面wTx+b=0的位置。这一性质在后续讨论中带来很大便利。
1、 最优间隔分类器
最优间隔分类器可以看做是支撑向量机的前身,是一种学习算法,选择特定的w和b,使几何间隔最大化。最优分类间隔是下述这样的优化问题:
即选择γ,w,b使γ最大,同时满足条件:所选取的最大几何间隔必须保证每个样本的几何间隔至少为γ。即,找到一个超平面,在将正负样本分开的同时,使超平面到正负样本间的距离尽可能大。
由于w和b可随意缩放,约束条件||w||=1,使得函数间隔等于几何间隔。但是这个约束本身是一个非常糟糕的非凸性约束。要求解的参数w在一个球体表面,如果想得到一个凸优化问题,必须保证如梯度下降算法这种局部最优值搜索算法不会找到局部最优值,而非凸性约束不能满足这个条件,所以需要改变优化问题。
为了解决上述问题,提出下面的最优化问题:
即将函数间隔除以||w||的值最大化,而这个值其实就是几何间隔,只是上一个优化问题的另一种表述。最优化目标是,最大化几何间隔,同时保证函数间隔不小于γ^,即求最大的γ^,但是γ^上限是最小的函数间隔的值。
对w添加约束条件:γ^ = 1,即函数间隔为1,即使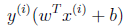
这是一个凸优化问题,且没有局部最优值,可以通过梯度下降找到全局最优值。
2、 原始优化问题&对偶优化问题(KKT条件)
原始问题
如要求下式的值:
即最小化函数f(w),并满足约束条件hi(w)=0,可以将hi写成0向量。
创建拉格朗日算子:
即等于原始目标函数加限制函数的线性组合,其中参数β称为拉格朗日乘数。
则,如果对下式求偏导数置为0,即可求出解:
对上述两个偏导数方程求解,检查得到的解是否为最小值即可。
拉格朗日乘数法的一般形式,也称为原始问题:
此时,拉格朗日算子为:
此时α和β为拉格朗日乘数,定义:
上式中的p表示原始问题(primal),
如果w违反了约束条件,即gi(w)>0或hi(w)!=0,那么上式变成:
上式中从(1)到(2)的解释为:若gi(w)>0,那么只要使αi无穷大,θp(w)就会无穷大;同理,若hi(w)!=0,只要使βi相应取无穷大(hi(w)>0)或无穷小(hi(w)<0),θp(w)也会无穷大。
反之,若w满足约束条件,那么θp(w) = f(w),所以可得:
那么,求min f(w)就是求下式的值,定义为p*:
对偶问题
定义:
对其取最大值,即给出对偶优化问题,定义为d*:
从公式上看,对偶问题就是把原始问题中的min,max换了顺序。
可得:
原始问题和对偶问题获得相同解的条件:
令f为凸函数(凸函数的hessian 矩阵是半正定的,H>=0,即开口朝上的碗状函数)
假设hi为仿射函数,即
假设gi是严格可执行的,即存在w,使得对于所有i,gi(w)<0
在上述条件下,存在w*,α*,β*,其中w*是原始问题的解,α*,β*是对偶问题的解,并且:
此外,还要满足条件:
这些条件被称为KKT互补条件。
KKT中的隐含条件:
如果αi>0 => gi(w*)=0,但是一般来说αi>0 <=> gi(w*)=0
当gi(w*)=0,称gi(w*)为活动约束。
3、 SVM对偶问题
最优间隔分类器:
将约束改写为:
又通过KKT条件,αi>0 => gi(w,b)=0,即活动约束
gi(w,b)=0 <=> y(i)(wTx(i)+b)=1,即函数间隔为1
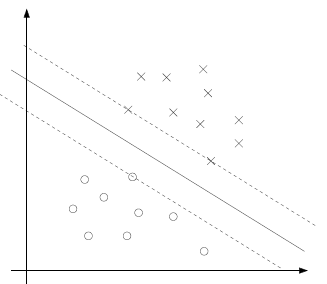
给出例子如下图:
图中的圈和叉即正负样本,实线即w,b确定的分隔线,虚线即函数间隔为1的点所构成的线。看出有三个样本的函数间隔为1,其他样本的函数间隔大于1。
通过KKT条件,这些函数间隔为1的样本对应的拉格朗日乘数一般不等于0,即αi>0。这个函数间隔为1的样本称为支撑向量。支撑向量数量很少,所以多数的αi=0,那么反推可得,αi=0,对应的样本不是支撑向量。
对最优间隔优化问题建立拉格朗日算子:
由于这个问题只有不等式约束,所以没有β。
为了使拉格朗日算子最小,因为它是w,b的函数,对w,b求偏导数并设为0。
推出:
w就是输入特征向量的线性组合。对b求偏导:
将w代入拉格朗日算子,即代入||w||=wTw,化简后得到:
根据对b求偏导的结果,最后一项为0,得到:
将上式表示为W(α),对偶问题就是:
所有优化问题都是针对w进行了,b只是一个参数。
为了解决上述对偶问题,求出参数α*,而求出α,即可通过上面w的公式求出w,求出α和w后,容易求出b,因为w决定了超平面的斜率,那么根据最优间隔,将α和w代入原始问题,就容易求出b了,如下式:
这个公式的直观理解就是,找到最差的样本(离得最近的正负样本),根据它们的位置,可求出超平面的位置。
4、 核方法
可以将上面整个算法表示成内积的形式:
x(i)Tx表示为新输入的x和训练样本x的内积的和。
在SVM特征空间中,由于训练样本的维数可能会很高,核方法可以高效计算内积的表示方法,但是仅对一些特定的特征空间成立。
浏览整个SVM计算过程,所有步骤都可以不直接计算x(i),而通过计算特征向量的内积得到结果,所以核方法被引入。
该算法另一个性质就是,由于函数间隔为1的样本只占训练集的一小部分,大多数αi=0,计算w时计算量小。








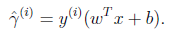
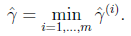
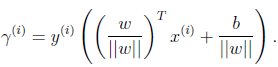
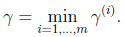

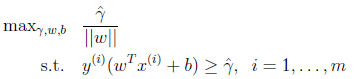
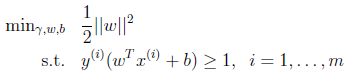
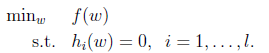
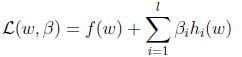
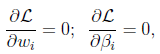


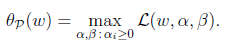
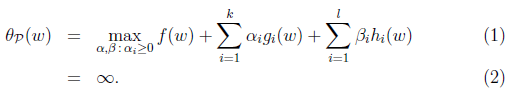
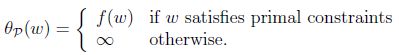
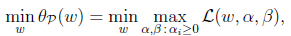
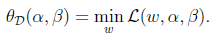
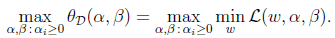
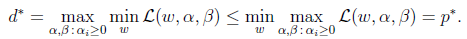
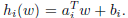
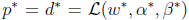

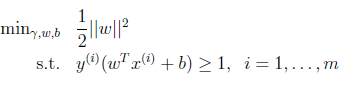
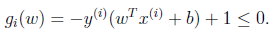
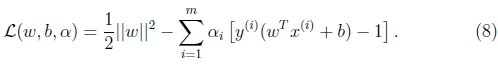
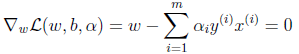
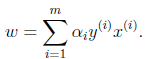
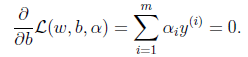
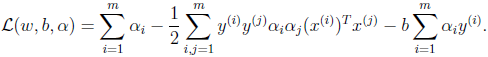
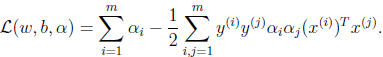

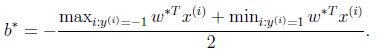
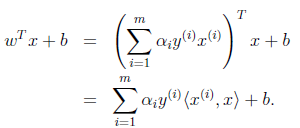
















 3463
3463

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








